转载

经典的排序算法

冒泡排序也叫起泡排序，大家都知道，学C语言那会的循环结构就那这个做的例子，冒泡排序过程很简单，但是效率太低。

1：简要过程：

首先将一个记录的关键字和第二个记录的关键字比较若为逆序将两个记录交换，然后比较第二个记录和第三个记录的关键字....,直到n-1个记录呢第n个记录的关键字进行比较，上述过称作一趟冒泡排序，然后进行第二趟，对n-1个记录进行操作...（可以不安这种方法来，实际应用中可以逆序也可以正序，因为比较简单，所以不再多说）

2：排序效率：

如果开始的时候需要排序的元素是正序，则只要一趟，需要n-1次的关键字比较，如果为逆序要进行n(n-1)/2次的比较，所以时间复杂度是O(n ² )，所以效率超级的低，一般不建议使用

3：排序过程图：

经典的排序算法

4：具体算法实现（可以有多种形式）：

 1 //冒泡排序   2 void bubbling(int arr[], int n){  3     int i,j,k;  4     for(i = 0; i < n; i++){  5         for(j = i+1;j < n;j++){  6             if(arr[i] > arr[j]){  7                 k = arr[i];  8                 arr[i] = arr[j];  9                 arr[j] = k; 10             } 11         } 12     } 13 }

二、直接选择排序

是一种选择排序，总的来说交换的少，比较的多，如果排序的数据是字符串的话比建议使用这种方法。

1：简要过程：

首先找出最大元素，与最后一个元素交换（arr[n-1]），然后再剩下的元素中找最大元素，与倒数第二个元素交换....直到排序完成。

2：排序效率：

一趟排序通过n-1次的关键字比较，从n-i-1个记录中选择最大或者最小的元素并和第i个元素交换，所以平均为n(n-1)/2，时间复杂度为O(n ² )，也不是个省油的灯，效率还是比较低。

3：排序过程图：（选择小元素）

经典的排序算法

4：具体算法实现：

 1 //直接选择排序   2 void directDialing(int arr[], int n){  3     int i,j,k,num;  4     for(i = 0; i < n; i++){  5         num = 0;  6         for(j = 0; j < n-i; j++){  7             if(arr[j] > arr[num]){  8                 num = j;  9             }     10         } 11         k = arr[n-i-1]; 12         arr[n-i-1] = arr[num]; 13         arr[num] = k; 14     } 15 }

三、直接插入排序

是一种简单的排序方法，算法简洁，容易实现

1：简要过程：

每步将一个待排序元素，插入到前面已经排序好的元素中，从而得到一个新的有序序列，直到最后一个元素加入进去即可。

2：排序效率：

空间上直接插入排序只需要一个辅助空间，时间上：花在比较两个关键字的大小和移动记录，逆序时比较次数最大：（n+2）(n-1)/2，平均：n ^2/ 4，所以直接插入排序时间复杂度也是O(n ² )

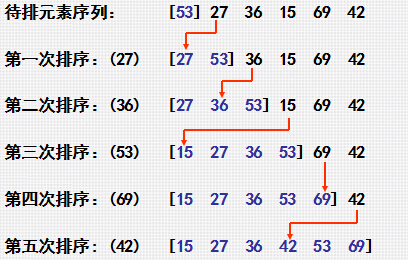
3：排序过程图：

经典的排序算法

4：具体算法实现：

 1 //直接插入排序  2 void  insert(int arr[], int n){  3     int m,i,k;  4     for(i = 1; i < n; i++){  5         m = arr[i];  6         for(k = i-1; k >= 0; k--){  7             if(arr[k] > m){  8                 arr[k+1] = arr[k];              9             }else{ 10                 break; 11             } 12         } 13         arr[k+1] = m; 14     } 15 }