面试毒瘤 之 反转二叉树
前一阵homebrew作者面试谷歌被拒,原因是这位老兄无法反转出二叉树。

面试前端攻城狮,请先反转二叉树。
面试.net程序猿,请先反转二叉树。
面试技术主管,请先不用递归反转二叉树。
面试CTO,请先不用递归反转二叉树。
俺无意评断谷歌和众多公司的用人标准是否合理,但反转二叉树确实是软件研发行业比较普遍的面试题。
废话了一堆,进入正题
先定义二叉树类
public class BinaryTreeNode<T> { public string Name { get; set; } public T Data { get; set; } public BinaryTreeNode<T> Left { get; set; } public BinaryTreeNode<T> Right { get; set; } private bool _isLeaf; public bool IsLeaf { get { _isLeaf = (Left == null && Right == null); return _isLeaf; } } public BinaryTreeNode(string name, T data = default(T)) { Name = name; Data = data; } public BinaryTreeNode<T> CreateAndJionLeft(string name, T data = default(T)) { return Left = new BinaryTreeNode<T>(name, data); } public BinaryTreeNode<T> CreateAndJionRight(string name, T data = default(T)) { return Right = new BinaryTreeNode<T>(name, data); } }
Name和Data是二叉树内部元素,根据需求调整即可,CreateAndJionLeft表示将左边子节点加入当前节点,也可在外部调用端实例化子节点。
接下来是二叉树常用的几种遍历方式:前序遍历,中序遍历,后序遍历,逐层遍历
/// <summary> /// 前序遍历 /// </summary> public void PreOrderTraversal() { if (this != null) { Trace.WriteLine(Name); } if (Left != null) { Left.PostOrderTraversal(); } if (Right != null) { Right.PostOrderTraversal(); } } /// <summary> /// 中序遍历 /// </summary> public void InOrderTraversal() { if (Left != null) { Left.PostOrderTraversal(); } if (this != null) { Trace.WriteLine(Name); } if (Right != null) { Right.PostOrderTraversal(); } } /// <summary> /// 后序遍历 /// </summary> public void PostOrderTraversal() { if (Left != null) { Left.PostOrderTraversal(); } if (Right != null) { Right.PostOrderTraversal(); } if (this != null) { Trace.WriteLine(Name); } } /// <summary> /// 逐层遍历 /// </summary> public void Traversal() { Queue<BinaryTreeNode<T>> nodeQueue = new Queue<BinaryTreeNode<T>>(); nodeQueue.Enqueue(this); while (nodeQueue.Count > 0) { BinaryTreeNode<T> temp = nodeQueue.Peek(); Trace.WriteLine(temp.Name); nodeQueue.Dequeue(); if (temp.Left != null) { nodeQueue.Enqueue(temp.Left); } if (temp.Right != null) { nodeQueue.Enqueue(temp.Right); } } }
递归实现反转二叉树
/// <summary> /// 反转二叉树(递归) /// </summary> public BinaryTreeNode<T> ReverseWithRecursive() { if (this == null) { return null; } if (!(Left == null && Right == null)) { BinaryTreeNode<T> temp = Right;//左右节点反转 Right = Left; Left = temp; if (Left != null) Left = Left.ReverseWithRecursive();//递归反转左子节点 if (Right != null) Right = Right.ReverseWithRecursive();//递归反转右子节点 } return this; }
非递归方式实现反转二叉树
/// <summary> /// 反转二叉树(非递归) /// </summary> /// <returns></returns> public BinaryTreeNode<T> Reverse() { if (this == null) { return null; } Queue<BinaryTreeNode<T>> nodeQueue = new Queue<BinaryTreeNode<T>>(); nodeQueue.Enqueue(this); while (nodeQueue.Count > 0) { BinaryTreeNode<T> node = nodeQueue.Peek(); nodeQueue.Dequeue(); BinaryTreeNode<T> tempNode = node.Right;//左右节点反转 node.Right = node.Left; node.Left = tempNode; if (node.Left != null) { nodeQueue.Enqueue(node.Left); } if (node.Right != null) { nodeQueue.Enqueue(node.Right); } } return this; }
定义一个队列来临时存储即将反转的节点。获取队列中存储的节点,获取到一个节点后队列中的此节点已无用将其删除,然后把获取到的节点的左右子节点反转,将反转后的左右子根节点都放入队列用于下一次循环。重复执行直到反转完所有树节点。
客户端调用
//创建二叉树 BinaryTreeNode<int> tree = new BinaryTreeNode<int>("0");//rootNode BinaryTreeNode<int> n01 = tree.CreateAndJionLeft("01"); BinaryTreeNode<int> n02 = tree.CreateAndJionRight("02"); BinaryTreeNode<int> n011 = n01.CreateAndJionLeft("011"); BinaryTreeNode<int> n012 = n01.CreateAndJionRight("012"); BinaryTreeNode<int> n021 = n02.CreateAndJionLeft("021"); BinaryTreeNode<int> n0211 = n021.CreateAndJionLeft("0211"); BinaryTreeNode<int> n0212 = n021.CreateAndJionRight("0212"); //遍历输出 tree.Traversal(); //反转二叉树并遍历输出 BinaryTreeNode<int> treeReverse = tree.Reverse(); treeReverse.Traversal();
反转前
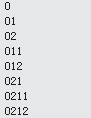
反转后

转载请注明地址:http://www.cnblogs.com/wintersoft/p/4676124.html
正文到此结束
热门推荐
相关文章
Loading...










![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

