转载

.NET平台开源项目速览(11)KwCombinatorics排列组合使用案例(1)

今年上半年，我在KwCombinatorics系列文章中，重点介绍了KwCombinatorics组件的使用情况，其实这个组件我5年前就开始用了，非常方便，麻雀虽小五脏俱全。所以一直非常喜欢，才写了几篇文章推荐给大家。最近在计算足球彩票结果组合过程中，使用的到了其功能，生成排列，非常具有代表性，而且也有网友咨询过类似的问题，所以就封装为扩展方法，方便调用。

NET开源目录: 【目录】本博客其他.NET开源项目文章目录

彩票数据资料目录：【目录】C#搭建足球赛事资料库与预测平台与彩票数据分析目录

本文原文地址: .NET平台开源项目速览(11)KwCombinatorics排列组合使用案例(1)

1.KwCombinatorics基本介绍

KwCombinatorics，它是.NET平台一个高效的生成排列组合序列的开源类库，它提供了4种生成排列与组合序列的方式。虽然原理和功能都很简单，但是这个类库在软件测试、组合数学以及密码学等方面都有很大的用处。很早就接触了这个类库，以前在一些小程序中也使用过，有时候为了遍历所有可能的组合，自己去写循环，生成，的确很繁琐，有了KwCombinatorics 之后，都变得简单写了，接下来将详细介绍该类库的使用。

KwCombinatorics类库的主页是： http://kwcombinatorics.codeplex.com/

关于 KwCombinatorics基本使用入门的文章有：

1. 【原创】开源.NET排列组合组件KwCombinatorics使用(一)组合生成

2. 【原创】开源.NET排列组合组件KwCombinatorics使用(二)排列生成

3. 【原创】开源.NET排列组合组件KwCombinatorics使用(三)笛卡尔积组合

2.足球彩票排列组合应用

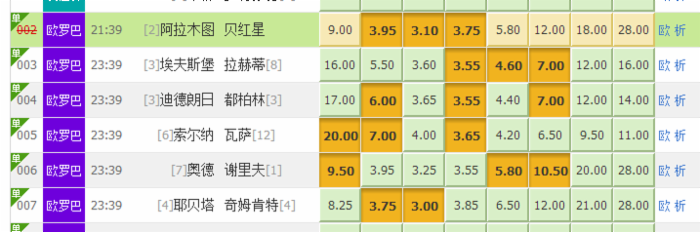
在足球彩票玩法中，经常要选择几场比赛，以及每场比赛不同的结果组合，进行投注，这个时候就要生成所有的排列组合了，以便进行下一步的平衡投注计算。例如，看下面一个截图：

.NET平台开源项目速览(11)KwCombinatorics排列组合使用案例(1)

例如，上午选择了3场比赛，前2场，每场选择2个结果，第三场做胆，进行3串1玩法，当然这里的例子很简单，大家脑袋想一想就知道是4个结果。如果是其他玩法，每个有3，4个选择，有5串1 ，那就麻烦了，何苦都必须要自动生成出组合来。所以必须得考虑一个通用的情况。而且在进行预测以及分析的时候，通常要对包含所有结果的几场比赛进行串分析，就需要计算所有排列组合的结果形式了例如下面这种总进球的多串1选择：

.NET平台开源项目速览(11)KwCombinatorics排列组合使用案例(1)

3.排列组合生成代码与测试

3.1 N场单个玩法所有结果的组合

比如胜平负有3个玩法，【3，1，0】，那么我有N场比赛，要进行串组合，计算所有的组合情况。写一个通用的函数，使用KwCombinatorics的笛卡尔积来完成，直接看代码和注释，注意使用之前要引用对应的dll和命名空间：

/// <summary>单个不同玩法，任意场次数的结果全部结果组合</summary> /// <typeparam name="T">结果类型，主要分字符串，整数</typeparam> /// <param name="source">该玩法的所有结果列表</param> /// <param name="count">场次数量：每一个场次都可能会出现source中的结果</param> /// <returns>所有组合的列表</returns> public static IEnumerable<List<T>> PermuteResultForSingle<T>(this List<T> source, int count) {  //实例化N场比赛的所有结果数组，每一个List都包括所有结果  List<T>[] sourceList = new List<T>[count];  Int32[] sizes = new Int32[count];   for (int i = 0; i < count; i++)  {   sourceList[i] = source;   sizes[i] = source.Count;  }  //使用笛卡尔积的形式来生成  var pt = new Product(sizes);  //依次生产所有组合，每一个组合都是结果的集合  foreach (var row in pt.GetRows())  {   yield return Product.Permute(row, sourceList);  } }

考虑到调用方便，这里写成了扩展方法，并使用了泛型，也就是说可以直接处理整数结果形式，也可以处理汉字字符串结果形式。那我们进行一下测试看看。

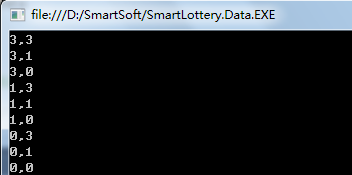
先看测试代码，我们假设胜平负玩法，2场比赛，应该是有9种结果：

static void Test1() {  //先定义每一个玩法的所有结果类型，胜平负有3个结果  var result = new List<Int32>() { 3,1,0};  //直接扩展方法计算，并传入场次数量参数，我们计算2场的所有组合  var combList = result.PermuteResultForSingle<Int32>(2);  foreach (var item in combList)  {   //将结果转换为字符串依次打印   //ArrayToString是一个将数组列表转换为字符串的扩展方法   Console.WriteLine(item.ArrayToString());  } }

看看结果：

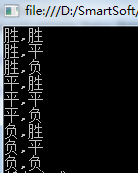
.NET平台开源项目速览(11)KwCombinatorics排列组合使用案例(1)

其实还可以处理字符串类型的情况，例如我们把代码改成这样：

var result = new List<String>() { "胜","平","负"}; //直接扩展方法计算，并传入场次数量参数，我们计算2场的所有组合 var combList = result.PermuteResultForSingle<String>(2); foreach (var item in combList) {  //将结果转换为字符串依次打印   Console.WriteLine(item.ArrayToString()); }

结果如下，当然你可以修改数量，计算更多复杂的情况，一一进行处理。

.NET平台开源项目速览(11)KwCombinatorics排列组合使用案例(1)

3.2 混合玩法的多个结果组合

在竞彩的混投玩法中，可以选择任意场次的不同玩法进行组合，比如，你A比赛可以选择胜平负结果，而B比赛选择大小球，然后串起来进行投注。情况有时候会更复杂，这种情况下，玩家为了刺激，会适当增加结果数量，然后进行串投注。其实整体思路和3.1差不多，只不过由于每个玩法的结果类型不一样，需要将参数转换为object，才更好处理。看看代码，也是扩展方法：

/// <summary>混合不同玩法，任意场次的多个结果的组合</summary> /// <param name="source">场次按顺序选择的玩法的所有结果列表</param> /// <returns></returns> public static IEnumerable<List<Object>> PermuteResultForMixture(this List<Object>[] source) {  //初始化所有场次玩法结果的数据  Int32[] sizes = new Int32[source.Length];  for (int i = 0; i < source.Length; i++) sizes[i] = source[i].Count;  //使用笛卡尔积，只不过这里都是Object，不在针对同一种玩法了  var pt = new Product(sizes);  foreach (var row in pt.GetRows())  {   yield return Product.Permute(row, source);  } }

看看实际的测试结果，当然你也可以把所有玩法都搞一样的，相对是同一种玩法的N场比赛，选择不同部分结果进行的组合了：

//胜平负场次的结果选择 var R1 = new List<Object>() { "胜","平"}; //总进球数结果的选择 var R2 = new List<Object>() { 2,3,4 }; //半全场结果的选择 var R3 = new List<Object>() { "胜负" ,"平负"}; //综合所有选择 var result = new List<Object>[] { R1, R2, R3 }; //计算所有组合 var combList = result.PermuteResultForMixture(); foreach (var item in combList) {  //打印组合，逗号分割，应该有2*3*2=12种组合  Console.WriteLine(item.ArrayToString()); }

看结果：

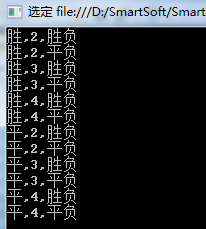
.NET平台开源项目速览(11)KwCombinatorics排列组合使用案例(1)