K-均值聚类算法
K-均值聚类算法
聚类是一种无监督的学习算法,它将相似的数据归纳到同一簇中。K-均值是因为它可以按照k个不同的簇来分类,并且不同的簇中心采用簇中所含的均值计算而成。
K-均值算法
算法思想
K-均值是把数据集按照k个簇分类,其中k是用户给定的,其中每个簇是通过质心来计算簇的中心点。
主要步骤:
- 随机确定k个初始点作为质心
- 对数据集中的每个数据点找到距离最近的簇
- 对于每一个簇,计算簇中所有点的均值并将均值作为质心
-
重复步骤2,直到任意一个点的簇分配结果不变
具体实现
from numpy import * import matplotlib import matplotlib.pyplot as plt def loadDataSet(fileName): #general function to parse tab -delimited floats dataMat = [] #assume last column is target value fr = open(fileName) for line in fr.readlines(): curLine = line.strip().split('/t') fltLine = map(float,curLine) #map all elements to float() dataMat.append(fltLine) return dataMat def distEclud(vecA, vecB): return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB) def randCent(dataSet, k): n = shape(dataSet)[1] centroids = mat(zeros((k,n)))#create centroid mat for j in range(n):#create random cluster centers, within bounds of each dimension minJ = min(dataSet[:,j]) rangeJ = float(max(dataSet[:,j]) - minJ) centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1)) return centroids def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent): m = shape(dataSet)[0] clusterAssment = mat(zeros((m,2)))#create mat to assign data points #to a centroid, also holds SE of each point centroids = createCent(dataSet, k) clusterChanged = True while clusterChanged: clusterChanged = False for i in range(m):#for each data point assign it to the closest centroid minDist = inf; minIndex = -1 for j in range(k): distJI = distMeas(centroids[j,:],dataSet[i,:]) if distJI < minDist: minDist = distJI; minIndex = j if clusterAssment[i,0] != minIndex: clusterChanged = True clusterAssment[i,:] = minIndex,minDist**2 for cent in range(k):#recalculate centroids ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#get all the point in this cluster centroids[cent,:] = mean(ptsInClust, axis=0) #assign centroid to mean print ptsInClust print mean(ptsInClust, axis=0) return return centroids, clusterAssment def clusterClubs(numClust=5): datList = [] for line in open('places.txt').readlines(): lineArr = line.split('/t') datList.append([float(lineArr[4]), float(lineArr[3])]) datMat = mat(datList) myCentroids, clustAssing = biKmeans(datMat, numClust, distMeas=distSLC) fig = plt.figure() rect=[0.1,0.1,0.8,0.8] scatterMarkers=['s', 'o', '^', '8', 'p', / 'd', 'v', 'h', '>', '<'] axprops = dict(xticks=[], yticks=[]) ax0=fig.add_axes(rect, label='ax0', **axprops) imgP = plt.imread('Portland.png') ax0.imshow(imgP) ax1=fig.add_axes(rect, label='ax1', frameon=False) for i in range(numClust): ptsInCurrCluster = datMat[nonzero(clustAssing[:,0].A==i)[0],:] markerStyle = scatterMarkers[i % len(scatterMarkers)] ax1.scatter(ptsInCurrCluster[:,0].flatten().A[0], ptsInCurrCluster[:,1].flatten().A[0], marker=markerStyle, s=90) ax1.scatter(myCentroids[:,0].flatten().A[0], myCentroids[:,1].flatten().A[0], marker='+', s=300) plt.show() 结果

算法收敛
设目标函数为
$$J(c, /mu) = /sum _{i=1}^m (x_i - /mu_{c_{(i)}})^2$$
Kmeans算法是将J调整到最小,每次调整质心,J值也会减小,同时c和$/mu$也会收敛。由于该函数是一个非凸函数,所以不能保证得到全局最优,智能确保局部最优解。
二分K均值算法
为了克服K均值算法收敛于局部最小值的问题,提出了二分K均值算法。
算法思想
该算法首先将所有点作为一个簇,然后将该簇一分为2,之后选择其中一个簇继续进行划分,划分规则是按照最大化SSE(目标函数)的值。
主要步骤:
- 将所有点看成一个簇
- 计算每一个簇的总误差
- 在给定的簇上进行K均值聚类,计算将簇一分为二的总误差
- 选择使得误差最小的那个簇进行再次划分
- 重复步骤2,直到簇的个数满足要求
具体实现
def biKMeans(dataSet, k, distMeans=distEclud): m, n = shape(dataSet) clusterAssment = mat(zeros((m, 2))) # init all data for index 0 centroid = mean(dataSet, axis=0).tolist() centList = [centroid] for i in range(m): clusterAssment[i, 1] = distMeans(mat(centroid), dataSet[i, :]) ** 2 while len(centList) < k: lowestSSE = inf for i in range(len(centList)): cluster = dataSet[nonzero(clusterAssment[:, 0].A == i)[0], :] # get the clust data of i centroidMat, splitCluster = kMeans(cluster, 2, distMeans) sseSplit = sum(splitCluster[:, 1]) #all sse sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:, 0].A != i)[0], 1]) # error sse #print sseSplit, sseNotSplit if sseSplit + sseNotSplit < lowestSSE: bestCentToSplit = i bestNewCent = centroidMat bestClust = splitCluster.copy() lowerSEE = sseSplit + sseNotSplit print bestClust bestClust[nonzero(bestClust[:, 0].A == 1)[0], 0] = len(centList) bestClust[nonzero(bestClust[:, 0].A == 0)[0], 0] = bestCentToSplit print bestClust print 'the bestCentToSplit is: ',bestCentToSplit print 'the len of bestClustAss is: ', len(bestClust) centList[bestCentToSplit] = bestNewCent[0, :].tolist()[0] centList.append(bestNewCent[1, :].tolist()[0]) print clusterAssment clusterAssment[nonzero(clusterAssment[:, 0].A == bestCentToSplit)[0], :] = bestClust print clusterAssment return mat(centList), clusterAssment 结果
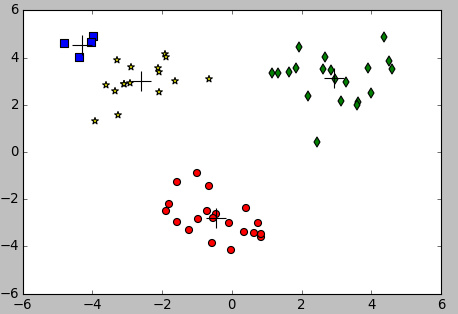
正文到此结束
热门推荐
相关文章
Loading...











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

