首先读入一个时间序列:从1946年1月到1959年12月的纽约每月出生人口数量(由牛顿最初收集)数据集可以从此链接下载(http://robjhyndman.com/tsdldata/data/nybirths.dat)。我们将数据读入R,并且存储到一个时间序列对象中,输入以下代码:
births<- scan("http://robjhyndman.com/tsdldata/data/nybirths.dat") birthstimeseries<-ts(births,frequency=12,start=c(1946,1)) 月度数据就设定frequency=12,季度数据就设定frequency=4;“start”参数来指定收集数据的第一年和这一年第一个间隔期。
接下来我们用plot函数绘制时间序列图:
plot.ts(birthstimeseries)
可以看到这个时间序列在一定月份存在的季节性变动:在每年的夏天都有一个出生峰值,在冬季的时候进入波谷。同样,这样的时间序列也可能是一个相加模型,随着时间推移,季节性波动时大致稳定的而不是依赖于时间序列水平,且对着时间的变化,随机波动看起来也是大致稳定的。
接下来我们来分解时间序列,时间序列分为:非季节性数据和季节性数据
一个非季节性时间序列包含一个趋势部分和一个不规则部分。分解时间序列即为试图把时间序列拆分成这些成分,也就是说,需要估计趋势的和不规则的这两个部分。
一个季节性时间序列包含一个趋势部分,一个季节性部分和一个不规则部分。分解时间序列就意味着要把时间序列分解称为这三个部分:也就是估计出这三个部分。
上述的婴儿出生是明显季节性时间序列,我们采用R提供的“decompose()”函数分解该时间序列:
birthstimeseriescomponents <- decompose(birthstimeseries)
估计出的季节性、趋势的和不规则部分现在被存储在变量birthstimeseriescomponents$seasonal, birthstimeseriescomponents$trend和 birthstimeseriescomponents$random 中。
我们可以分别画出这三部分,观察其特性:
plot(birthstimeseriescomponents)
图展现出了原始的时间序列图(顶部),估计出的趋势部分图(第二部份),估计出的季节性部分(第三个部分),估计得不规则部分(底部)。我们可以看到估计出的趋势部分从1947年的24下降到1948年的22,紧随着是一个稳定的增加直到1949年的27。
上述示例充分展示了时间序列的多模型加和性,该属性也是时间序列的一个很重要的属性,每拿到一个时间序列,我们首先需要判断该时间序列是否可以用相加模型来描述,在确定了加和属性后去考虑如何分解时间序列,以下举一个例子说明(澳大利亚昆士兰州海滨度假圣地的纪念品商店从1987年1月到1987年12月的每月销售数据)。我们首先画出该序列,找个整体的感知:
souvenir <- scan("http://robjhyndman.com/tsdldata/data/fancy.dat") souvenirtimeseries <- ts(souvenir, frequency=12, start=c(1987,1)) plot.ts(souvenirtimeseries) 结果如下:
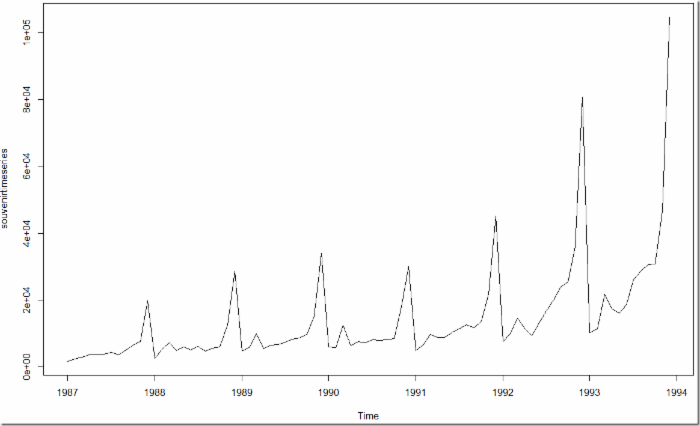
该序列看上去不适合时间,因为该序列的季节波动性和随机波动的大小随着时间序列逐步上升。为了使该序列符合标准的时间序列从而采用相加模型描述,我们对原始数据取自然对数进行转换:
logsouvenirtimeseries <- log(souvenirtimeseries) plot.ts(logsouvenirtimeseries)
结果如下:
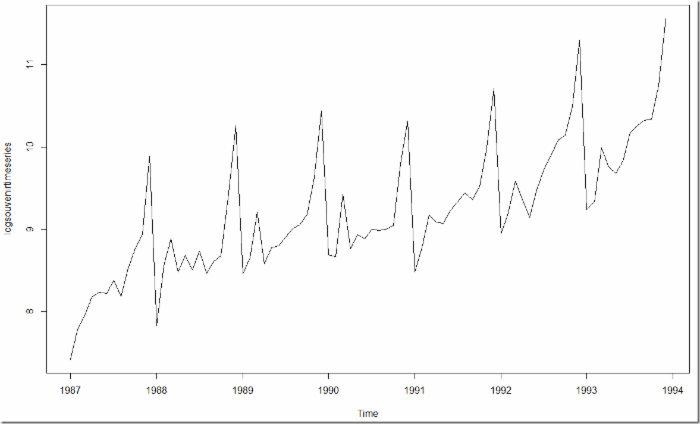
我们可以看到季节性波动和随机变动的大小在对数变换后的时间序列上,随着时间推移,季节性波动和随机波动的大小是大致恒定的,并且不依赖于时间序列水平。因此转换后的时间序列可以用相加模型进行描述,我们对变化后的序列进行分解:
logsouvenirtimeseriesComponents <- decompose(logsouvenirtimeseries) plot(logsouvenirtimeseriesComponents)
观察该图,我们也可以看出随着时间的推移,随机和季节的波动都是稳定的,再次证明我们的转换是有作用的。











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

