转载

数据结构之斐波那契查找

数据结构之--斐波那契查找

定义：相当于折半查找，一般将带比较的key值与第mid=（low+high）/2位置的元素比较，比较结果分为三种情况：

1），相等，mid位置的元素即为所求；

2），>，low=mid+1；

3），<，high=mid-1；

跟折半查找很相似，它是根据斐波那契数列的特点对有序表进行黄金分割。

图解：

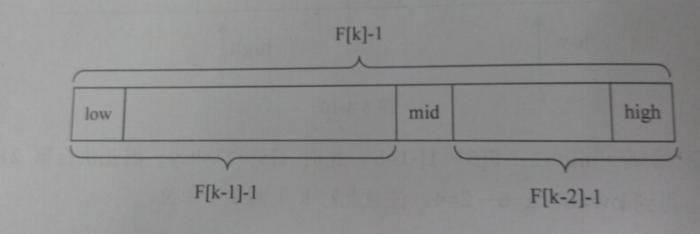
数据结构之斐波那契查找

时间复杂度：如果要查找的记录在右侧，则左边的数据都不用在哦按段了，不断反复进行下去，对处于当中的大部分数据源，其工作效率要高一些所以尽管斐波那契查找的时间复杂度也为O(logn)。但品均性能上来说，斐波那契查找要优于折半查找，可惜如果是最坏情况，比如这里key=1的时候，那么始终都处于左侧长半区在查找，则查找效率要低于折半查找。

还有一点比较关键，折半查找是进行假发与除法运算（mid={low+high}/2），插值查找进行复杂的四则运算（mid=low+(high-low)*(key-a[low])/(a[high]-a[low])），而斐波那契额查找只是最简单加减运算（mid=low+F[k-1]-1），在海量数据的查找过程中，这种细微的差别可能会影响最终的查找效率。

应该说“顺序表查找”、“折半查找”、“插值查找”这三种查找本质上是分隔点不同，各有优劣，实际开发过程中可根据实际情况中数据的综合特点再做出选择。

#include<stdio.h>

int F[] = {0,1,1,2,3,5,8,13,21,34,55};

int Binary_Search(int *a,int n,int key){

int low,mid,high,i,k;

low = 1;

high = n;

k = 0;

while(n>F[k]-1)

k++;

for(i=n;i<F[k]-1;i++)

a[i]=a[n];