【数据分析/挖掘必备知识】统计学之离散概率分布的运用

统计学之离散概率分布的运用

文章导航：

统计学之几何分布、二项分布及泊松分布

1 离散概率分布

1.1    定义

设离散型随机变量X所有可能得取值 X _i  (i=1,2,3…….n)，且事件{X=x _i }的概率为P{X=x _i }= p _i  ，此称为离散型随机变量的概率分布或分布列，即离散概率分布。用表格可表示：

作为一个离散概率分布，应满足以下两个性质:

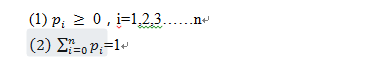
在日常生活中此类例子不胜枚举，比如，扔一枚或多枚硬币，出现正面朝上的次数。

1.2    基本概念

1.1.1     离散随机变量

若一个随机变量X的所有可能的取值为有限个或无限可数个， 则称它为离散型随机变量。例如，玩一次游戏机可获收益的金额。

1.1.2     期望

在概率论和统计学中，期望为期望值的简称，是指在一个离散型随机变量试验中每次可能结果的概率乘以其结果的总和。随机变量X的期望通常写作E(X)，但有时也会写作μ(缪)，也就是均值的符号。下面是E(X)的计算式：

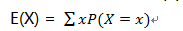
假设下表1为游戏机的概率分布：

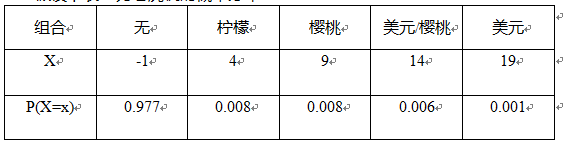
游戏机收益的期望：

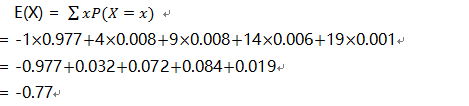
1.1.3     方差

方差是各个数据分别与其平均数之差的平方的和的平均数，用字母D表示。在概率论和数理统计中，方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。概率分布的方差通常写作Var(X)或D(X)，下面是Var(X)的计算式：

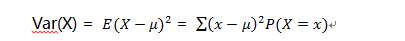
由上表1为例，游戏机收益的方差：

1.1.4     标准差

即方差的平方根，表示随机变量值与期望之间的距离。标准差通常用σ(西格玛)表示，计算式为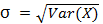： ，由上面求出的方差，可知游戏机收益的标准差是 1.642，这表示从平均情况老看，我们的每一局收益与期望收益-0.77之间的距离是1.642。

1.3    随机变量的线性关系

假设随机变量Y与游戏机收益的随机变量X满足Y=aX+b的线性关系，则Y的概率分布可用表2表示为：

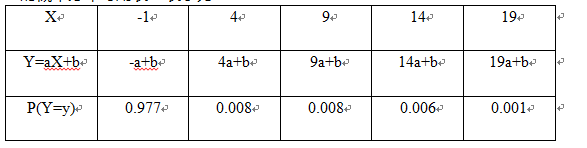
且随机变量Y的期望E(Y)和方差Var(Y)满足以下线性关系：

1.4    独立观察值

定义:具有与同一随机变量相同的概率分布且互不相干的观测值。例如，一台游戏机先后两次出现的收益结果。

观测值速算法求期望和方差：

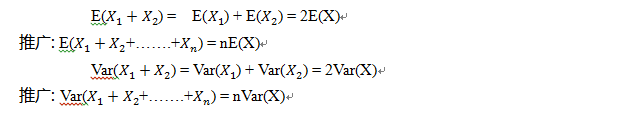
1.5    随机变量的独立性应用

如果X与Y是独立随机变量，则有：

E(X+Y) = E(X) + E(Y)

E(X-Y) = E(X) - E(Y)

Var(X+Y) = Var(X) + Var(Y)

Var(X-Y) = Var(X) + Var(Y)

同理，X与Y的线性变换的期望和方差：

E(aX+bY) = aE(X) + bE(Y)

E(aX-bY) = aE(X) - bE(Y)

Var(aX+bY) = Var(X) + Var(Y)

Var(aX-bY) = Var(X) + Var(Y)

随机变量的独立性应用的实例也不叫常见，例如，玩一次两台不同游戏机的总收益。

2、内容扩展

/**  * @ClassName ScoreUtil  * @Description 分数处理工具类  * @author candymoon  * @Date 2014-4-25  */ public class ScoreUtil {   /**    * 使用java正则表达式去掉多余的.与0    * @param s    * @return     */    public static  String subZeroAndDot(String s){     if(!s.isEmpty()&&s!=""){    if(s.indexOf(".") > 0){       s = s.replaceAll("0+?$", "");//去掉多余的0       s = s.replaceAll("[.]$", "");//如最后一位是.则去掉       //如果现在还包含小数部分     if(s.indexOf(".")>0){      double db = Double.valueOf(s);      float retscorce = (float)(Math.round(db*10))/10;      return retscorce+"";     }    }   }   return s;    }   /**   * @Title: caculateScoreByProportion   * @Description: 按比例计算出分数  * @author candymoon  * @date 2014-4-28 下午3:23:03  * @param curProportion  * @param curScorceInfo  * @return  */  public static String caculateScoreByProportion(String curProportion,String curScorceInfo){   //分数 当前分数为0分   if(!curScorceInfo.isEmpty()&&curScorceInfo!=""){    return "0";   }   float scorceInfo = Float.valueOf(curScorceInfo);   float proportion = Float.valueOf(curProportion)/100;   float retscorce = (float)(Math.round(scorceInfo*proportion*10))/10;   return retscorce+"";  }  /**   * @Title: addScore   * @Description: 计算2个得分  * @author candymoon  * @date 2014-4-28 下午3:51:03  * @param beforescorceInfo  * @param aftercorceInfo  * @return  */  public static String addScore(String beforescorceInfo,String aftercorceInfo){   float beforescorceInfo1 = Float.valueOf(beforescorceInfo);   float aftercorceInfo2 = Float.valueOf(aftercorceInfo);   return (beforescorceInfo1+aftercorceInfo2)+"";  }   /**    * 将double类型数据转换为百分比格式，并保留小数点前IntegerDigits位和小数点后FractionDigits位    * @author candymoon    * @param d    * @param IntegerDigits    * @param FractionDigits    * @return    */   public static String getPercentFormat(double d,int IntegerDigits,int FractionDigits){    NumberFormat nf = java.text.NumberFormat.getPercentInstance();     nf.setMaximumIntegerDigits(IntegerDigits);//小数点前保留几位    nf.setMinimumFractionDigits(FractionDigits);// 小数点后保留几位    String str = nf.format(d);    return str;   }   /**    *     * @param d    * @return    */   public static String getPercentFormat(double d){    DecimalFormat df = new DecimalFormat(".00");    String str = df.format(d);    float con = Float.valueOf(str);    con = con*100;    str = (int)con+"%";    return str;   }  /**   * 获取指定小数位的字符串   * @param fractionDigits (四舍五入)保留几位小数   * @return   */   public static String getFractionDigits(double dvalue,int fractionDigits){   String decimalFormat = "%."+fractionDigits+"f";   String valueString = String.format(decimalFormat,dvalue);   //System.out.println(valueString);   return valueString;   }  public static void main(String[] args) {   System.out.println(ScoreUtil.caculateScoreByProportion("40", "62"));   System.out.println(getPercentFormat(111.0123,3,3));   getFractionDigits(0.0,3);   //System.out.println(getFractionDigits(12438.45687,3));   //System.out.println(getFractionDigits(12438.00,3));     } 

/**  * 离散型概率分布（求期望、方差、标准差）  * @author 白宁超  * @2015-7-31下午2:51:07  */ public class DiscreteProbabilityDistribution {  /**   * 计算期望   * @param data 离散概率分布数据   * @return   */  public static double calculateExpectedValue(double[][] data){   int len = data[0].length;   double Ex = 0;//x分布期望值   //循环叠加计算期望值   for (int i = 0; i < len; i++) {    Ex += data[0][i]*data[1][i];   }   //并将结果保留3位小数（四舍五入）   String Ex_String = ScoreUtil.getFractionDigits(Ex, 3);   Ex = Double.valueOf(Ex_String);   System.out.println("期望："+Ex);   return Ex;  }  /**   * 计算方差   * @param data 离散概率分布数据   * @return   */  public static double calculateVariance(double[][] data){   double Ex = calculateExpectedValue(data);   double Ex2 = 0;//x平方分布的期望值   double variance = 0;//方差   int len = data[0].length;   //循环叠加计算期望值   for (int i = 0; i < len; i++) {    Ex2 += data[0][i]*data[0][i]*data[1][i];   }   //方差计算公式：D(X) = E(X2)- E(X)*E(X)   variance = Ex2-(Ex*Ex);   //并将结果保留3位小数（四舍五入）   String variance_String = ScoreUtil.getFractionDigits(variance, 3);   variance = Double.valueOf(variance_String);   System.out.println("方差："+variance);   return variance;  }  /**   * 计算标准差   * @param data 离散概率分布数据   * @return   */  public static double calculateStandardDeviation(double[][] data){   double variance = calculateVariance(data);   double sd = Math.pow(variance, 0.5);//求一个数的开根号值   //并将结果保留3位小数（四舍五入）   String sd_String = ScoreUtil.getFractionDigits(sd, 3);   sd = Double.valueOf(sd_String);   System.out.println("标准差："+sd);   return sd;  }  /**   * 计算离散概率分布的期望、方差和标准差   * @param data 概率分布数据   * @return 包含期望、方差和标准差的数组 double[]{Ex,variance,sd};   */  public static double[] calculateEVAndVarAndSD(double[][] data){   //变量定义   int len = data[0].length;   double Ex = 0;//x分布期望值   double Ex2 = 0;//x平方分布的期望值   double variance=0;//方差   //计算x期望值和项x平方的期望值，并将结果保留3位小数（四舍五入）   for (int i = 0; i < len; i++) {    Ex += data[0][i]*data[1][i];    Ex2 += data[0][i]*data[0][i]*data[1][i];   }   String Ex_String = ScoreUtil.getFractionDigits(Ex, 3);   Ex = Double.valueOf(Ex_String);   //计算方差并将结果保留3位小数（四舍五入）   variance = Ex2-(Ex*Ex);   String variance_String = ScoreUtil.getFractionDigits(variance, 3);   variance = Double.valueOf(variance_String);   //计算标准差并将结果保留3位小数（四舍五入）   double sd = Math.pow(variance, 0.5);//求一个数的开根号值   String sd_String = ScoreUtil.getFractionDigits(sd, 3);   sd = Double.valueOf(sd_String);   System.out.println("期望:"+Ex+" 方差:"+variance+" 标准差:"+sd);   return new double[]{Ex,variance,sd};  }  /**   * @param args   */  public static void main(String[] args) {   double[][] data = new double[][]{{1,2,3,4,5},{0.2,0.2,0.2,0.2,0.2}};   calculateStandardDeviation(data);   calculateEVAndVarAndSD(data);  } 

注：PPT下载（提取码：4849）