How-Old维护小记
简介
前几版How-Old发布后，不少用户反馈，在显示结果的页面中，用于标注前面人年龄的标签，会遮挡住后面的人的脸。这是因为我们最初采用固定偏移的方式来放置年龄标签。
而怎么样让标签不遮挡住其他人的脸，则成为一个有趣的问题。最近我们发布了一次How-Old更新，正好用这篇文章，来记录一下我们对这一问题的实现。
先直观的看一下新版本的改变（左旧 右新）：
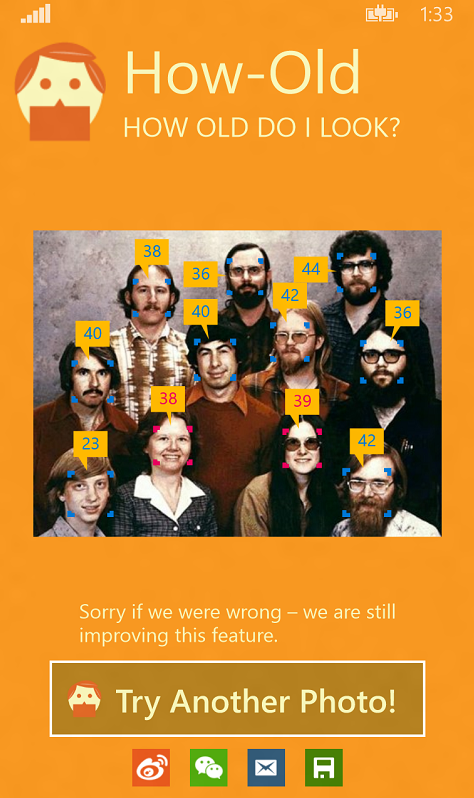
问题
我们来抽象一下这个问题。
在服务器端识别出了照片中的脸后，会将识别数据传回客户端，其中包含了每个脸的边缘矩形的位置和大小信息（FaceRect）。
然后我们要为每个脸添加对应的标签（LabelRect）。LabelRect和FaceRect两两不重合，LaebelRect自身两两不重合。（FaceRect本身是有可能重合的）
并且我们希望每个标签都尽量离对应的脸比较近。
以上就是比较核心的问题描述。此外我们在实现中还加入了一些小小的增强体验的条件，在正文中会为大家叙述。
算法
我们采用了平面分割标记的算法来布置LabelRect。
对于每个Rect（包括LabelRect，FaceRect），我们需要它的中心点RectCenter(x, y)，我们需要确定的也正是每个LabelRect的中心点。
简单的分析一下，我们发现在每个Rect周围一定的区域内，是不能布置LabelCenter的，否则就会导致重合。
如下图所示：
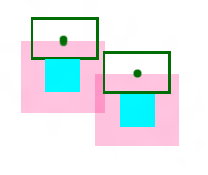
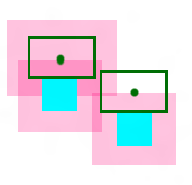
亮蓝色是FaceRect，墨绿色是LabelRect，中间的绿点是LabelRect的中心。
粉红色的半透明区域就是那些不能放置LabelCenter的。这个区域的大小也由LabelRect的大小确定（此例中LabelRect的大小是我们设定好的，每个都一样）。
粉红区域是有FaceRect分别向左右各扩展LabelRect.Width/2，向上下各扩展LabelRect.Height/2确定的。可以看出只要在粉红区域以外放置LabelRect，就必然不会导致LabelRect和FaceRect相交。
我们简单的把每个粉红区域叫做一个ForbidRect。
这样我们就只需要在ForbidRect的边界上选出最合适的点作为LabelCenter就行了（比如离FaceRect最近的点）。
但实际上上图还有问题。还要保证LabelRect彼此不相交呢？
上图应该是这样：
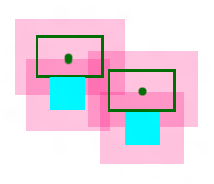
为了方便，我们采用依次布置LabelRect的方式，先布置的一旦布置好就不再移动了，后布置的受限于前面布置的。（即不采用“在一个漏斗里倒入小球，小球会彼此挤开”这种方式）
现在我们提供一种逐步布置的过程，直观的理解一下：
最初从服务器传回的FaceRect。
============================
得出最初的ForbidRect集。
============================
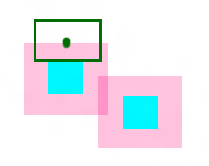布置第一个LabelRect。
============================
更新ForbidRect集。
============================
布置第2个LabelRect。
============================
再更新ForbidRect集就达到了我们之前那样的结果。
（此过程举例中先放哪个后放哪个，是随便选的）。
那，我们怎么确定该把LabelCenter放在哪呢？换言之，我们怎么出ForbidRect的边界上选出那个合适的点呢？
当时我们就想，怎么在非离散的二维平面上做这个？
然后我们采用了分割平面的方法，就像上图那些重叠的半透明的粉红色块一样，将平面分成一块块的来遍历。
Like this：
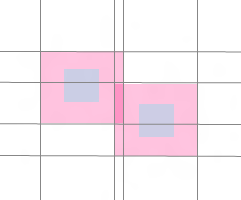（不重要的色块被淡化了。）
每个forbidRect都会引入4个分割线，横向俩，纵向俩。
同时每条分割线会包含引入这条线的ForbidRect编号，每条线都用一个二元组描述：
Tuple1= （offset, rect_id）。Offset是这条线 在垂直方向上距原点的偏移量 （就是“直线X=3”里面的那个“3”），rect_id就是引入它的ForbidRect编号。
横线，纵向分开统计。
举例：假设左上角那个forbidRect编号是0，右下角那个是1。当前纵向的分割线二元组数组为：L1 = {(1, 0), (5, 0), (4, 1), (8, 1)}
然后我们为了以防万一要处理一下，就是把偏移量相同的线归组（虽然不太可能有线重合，但这也是优化点之一，我们可以将forbidRect对齐到一些偏移量为某整数倍的位置）。
归组后的新二元组如下：
Tuple2=（offset，set<rect_id>）。二元组的第二个元素变成了forbidRect 编号的集合了。
此时我们有两个Tuple2数组了（横向的，纵向的），我们按照offset字段将它们排序（两个方向的分开进行）。
举例，排序后的纵向线的数组为：L2 = {(1, {0}), (4, {1}), (5, {0}), (8, {1})}
这时我们要遍历一下排序后的数组，收集一些信息，通过类似栈的方式获取每个forbidRect覆盖的分割线在分割线数组中的索引（从0开始）。因为分割线排好序了，我们就记一个区间好了。
举例：forbidRect 0 的“覆盖线”的索引区间为： [0, 2]。
但是我们是为了分割平面才引入的分割线，因为水平方向上索引为2的线（第三条线）之后已经不是forbidRect 0 的范围了，所以这个索引区间的意义实际上是[0, 2)——不再是分割线的索引，而是横向上的小平面区域的索引。
同时，我们还有一个映射M1：(index1, index2) -> isDirty。映射源是一个被横纵线分割出的小矩形（Cell）的横纵向索引，映射目标是一个boolean量，用来表示这个Cell是否属于一个ForbidRect。
举例：(0,0)->true, (1,0)->true, (2,0)->false. (2,2)->true.
做好这些准备后，就是我们最后的布局阶段了。
我们依照距离所有faceRect重心（是“重心”）最小的顺序为FaceRect排序，也就是越靠近中心的越先处理。
对每个faceRect，找到它的ForbidRect。通过ForbidRect在X Y方向上的“覆盖Cell”索引区间，找出位于该Forbidrect边界上的Cell。
举例：ForbidRect 0 边界上的Cell有：(0, -1) (1, -1) (-1, 0) (-1, 1) (2, 0) (2, 1) (0, 2) (1, 2)
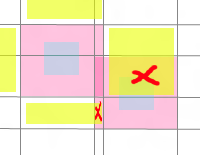
就是图中这四个黄色块标示的8个Cell（最左边和最上边的就为它们编号-1）。
===================================
其中有几个Cell是Dirty的：
===================================
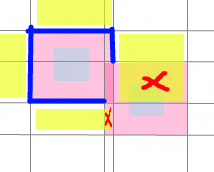
也就是说，我们只要在这6条线段（蓝色标出）上找LabelCenter就可以了
===================================
我们当前的策略是：先上，再左，再右，最后下方。
对每个线段，判断它的两个顶点，是在FaceRect与线段垂直的轴线的一左一右？一上一下？还是在同一侧？——这样就能判断最优的点（距离最近）。每个线段有一个最优解，再从中得出全局最优解。
（如果在上方就能得出这样的解，直接就用它做全局解。不然依次继续左、右、下方中找。下方的点，我们不喜欢，设置一个值去抑制它成为全局最优解）。
但，如果一个forbidRect四面受敌，一条这样的边界线段也没有怎么办呢？
此时我们通过一个forbidRect相交矩阵，广度优先，遍历每个和它直接或间接相接的forbidRect，从这些ForbidRect的边界线段上，找出最优的那个点，作为LabelCenter。
之后我们将这个LabelRect对应的ForbidRect加入ForbidRect集，并对下一个Face（按距重心排序地）进行同样的过程。直到所有Face都处理完成。
总结
这个算法的大致流程就是这样，其中也还有一些地方值得继续优化。当然我们还对标签大小，标签偏移等属性进行了微调。
希望这篇文章能抛砖引玉，如果大家有更好的算法或者想法，欢迎和我们交流。也欢迎下载最新版的How-Old进行各种各样图片的测试。
最后 向量子力学致敬:)
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
