转载

OpenGL绘制简单的参数曲线——两点三次Hermite曲线（一）

网上这类曲线绘制的文章非常多，但是大多都是代码一贴就完事了，甚至连参数怎么调也没说清楚。我翻阅了不少资料，这里做个汇总，主要也就介绍一下几类简单的曲线绘制，如Hermite曲线、Bezier曲线等。今天先说说Hermite曲线，基本上最常见的就是两点三次的Hermite曲线了。

按照惯例，我们先来介绍一下Hermite曲线的原理。 Hermite曲线是给定曲线段的两个端点坐标以及两端点处的切线矢量来描述的曲线。平面上一条三次参数曲线可以表示为：

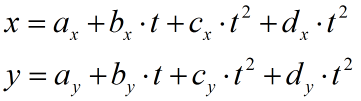
图1

空间Hermite曲线跟上述类似，只是加一个z分量。根据上式，该曲线的矢量表达式为：

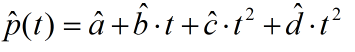
OpenGL绘制简单的参数曲线——两点三次Hermite曲线（一）

图2

这些带箭头的变量都是向量。我们根据几何定义，t=0时，曲线表达式的值就是 P ₀ 点，t=1时，曲线表达式的值就是 P ₁ 点。我们就得到了 P ₀ 、 P ₁ 、 P ₀ ' 、 P ₁ ' 的关系式，从而解得各个代数系数：

OpenGL绘制简单的参数曲线——两点三次Hermite曲线（一）

图3

于是，矩阵表达式为：

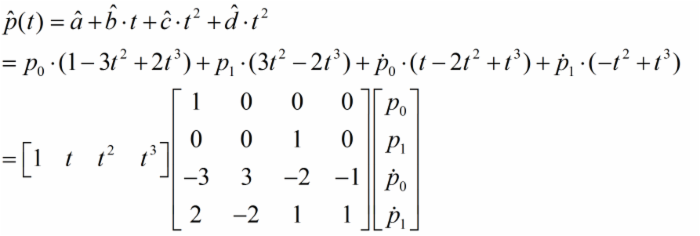
OpenGL绘制简单的参数曲线——两点三次Hermite曲线（一）

图4

中间的矩阵M是由初始条件确定的一个矩阵。写到这里我们已经具备了基础知识。这个二点三次的Hermite曲线主要有四个参数， P ₀ 和 P ₁ 分别表示起始和终点位置， P ₀ ' 和 P ₁ ' 分别表示起点和终点的方向（不过略微有点差异，大家可以根据程序自己调试感受下），下面我贴出代码，大家结合代码就能更理解了。

#include<math.h> #include <gl/glut.h> #include <iostream> using namespace std;  #define COUNT 20  struct Point2 {  float x;  float y; };  /*全局变量*/ float hermiteMP[4][2]; Point2 vec[COUNT];  /* q键和a键可以调节derP0x   * w键和s键可以调节derP0y   * e键和d键可以调节derP1x   * r键和f键可以调节derP1y   */ int derP0x = 100; int derP0y = 500; int derP1x = 50; int derP1y = -50;  /*矩阵M*/ float hermiteM[4][4] = {   {1, 0, 0, 0},  {0, 0, 1, 0},  {-3, 3, -2, -1},  {2, -2, 1, 1} };  /*矩阵M*矩阵P*/ void createMP(float hermiteP[][2]) {  memset(hermiteMP, 0, sizeof(hermiteMP));//初始化   for(int i = 0; i < 4; i++)  {   for(int j = 0; j < 2; j++)   {    for(int k = 0; k < 4; k++)    {        hermiteMP[i][j] += (hermiteM[i][k] * hermiteP[k][j]);    };    }  } }  /*求解P(t)*/ void creatPt(float hermiteP[][2]) {  vec[0].x=hermiteP[0][0];  vec[0].y=hermiteP[0][1];   float t = 0.0;      float deltaT = 1.0/COUNT;    for(int i = 1; i < COUNT; i++)   {   t += deltaT;   vec[i].x = hermiteMP[0][0] + hermiteMP[1][0]*t + hermiteMP[2][0]*t*t+ hermiteMP[3][0]*t*t*t;   vec[i].y = hermiteMP[0][1] + hermiteMP[1][1]*t + hermiteMP[2][1]*t*t + hermiteMP[3][1]*t*t*t;  }   vec[COUNT-1].x = hermiteP[1][0];  vec[COUNT-1].y = hermiteP[1][1]; }  void init() {  glClearColor(1.0, 1.0, 1.0, 0.0);  glShadeModel(GL_FLAT);  }  void reshape(int w, int h) {  glViewport(0, 0, (GLsizei)w, (GLsizei)h);  glMatrixMode(GL_PROJECTION);   glLoadIdentity();                 gluOrtho2D(-500, 500,-500, 500);     }  void display() {  glClear(GL_COLOR_BUFFER_BIT);   /*P0，P1，P0‘、P1’组成矩阵P*/  float hermiteP[4][2] = {   {0, 0},   {200, 0},   {derP0x, derP0y},   {derP1x, derP1y}  };   createMP(hermiteP);  creatPt(hermiteP);   glColor3f(1,0,0);  glLineWidth(3);    glBegin(GL_LINE_STRIP);   for(int i = 0; i < COUNT; i++)  {   glVertex2f(vec[i].x, vec[i].y);  }  glEnd();   glFlush();  glutSwapBuffers(); }  void keyboard(unsigned char key, int x, int y) {  if (key == 'q')   derP0x += 10;   if (key == 'a')   derP0x -= 10;   if (key == 'w')   derP0y += 10;   if (key == 's')   derP0y -= 10;   if (key == 'e')   derP1x += 10;   if (key == 'd')   derP1x -= 10;   if (key == 'r')   derP1y += 10;   if (key == 'f')   derP1y -= 10;   glutPostRedisplay(); }   int main(int argc, char** argv) {  glutInit(&argc, argv);  glutInitDisplayMode(GLUT_RGB | GLUT_DOUBLE);  glutInitWindowPosition(400,200);  glutInitWindowSize(500,500);  glutCreateWindow("Hermite曲线");  init();   glutDisplayFunc(display);    glutReshapeFunc(reshape);    glutKeyboardFunc(keyboard);  glutMainLoop();    return 0; }

正文到此结束