转载

排序算法之归并排序

一：要点

归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用 分治法（Divide and Conquer） 的一个非常典型的应用。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为 二路归并 。

二：归并排序思想

主要分为两步：1.折半划分 2.两两归并

折半划分：就是将1个长度为N的序列递归分成N个长度为1的序列。

例如下图，以N=8为例，不断递归分解直到成为长度为1的小序列

排序算法之归并排序

两两归并：将每个相邻的长度为n(n<N)序列归并为一个有序序列。

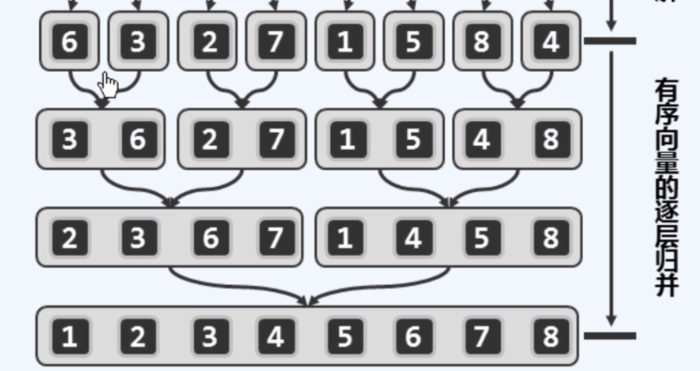
排序算法之归并排序

其中我们分解是使用递归，这个并不难：

void MergeSort(int arr[],int low,int high)//归并排序 {  int mid;  if(low < high)  {   mid = (low + high)/2;  //分解为两部分   MergeSort(arr,low,mid);  //使用递归对arr[low,mid]划分   MergeSort(arr,mid+1,high); //使用递归对arr[mid,high]划分  } }

归并排序中的难点主要在如何将相邻的两个有序序列归并成一个有序序列：

1.将两个有序序列的最小值比较，较小的在原序列删除并用新的数组记录。

2.不断重复1操作直到原来的两个有序序列删除到没有数据。

具体流程图如下：

排序算法之归并排序

这样的一个分解归并的思想来完成排序。

三：归并排序的C语言描述

算法步骤：

1.递归对数组进行分解，直到每个小序列长度为1

2.对每个相邻的小序列进行二路归并

2.1 申请辅助空间记录左边的小序列，比较辅助数组中的左边序列和右边序列的最小值，较小的记录在原数组

2.2 重复2.1操作直到左边序列和右边序列比较完毕，释放辅助数组空间。

3.排序完毕

完整排序C语言代码：

void Merge(int arr[],int low,int mid,int high)//归并 {  int i,j,k;  int *temp;  temp = (int*)malloc(sizeof(int)*MAX);//申请辅助数组temp记录左半边数组  for(i = low;i <= mid;temp[i] = arr[i++]);//填充temp  i = low,j = low,k = mid + 1;  while(j <= mid && k <= high) //当左边和右边都没有合并完时  {   if(temp[j] <= arr[k])   {    arr[i++] = temp[j++];   }   else   {    arr[i++] = arr[k++];   }  }  while(j <= mid) //右边合并完成，直接填充左边  {   arr[i++] = temp[j++];  }  while(k <= high)//左边合并完成，直接填充右边  {   arr[i++] = arr[k++];  }  free(temp); } void MergeSort(int arr[],int low,int high)//分解 {  int mid;  if(low < high)  {   mid = (low + high)/2;  //分解为两部分   MergeSort(arr,low,mid);  //使用递归对arr[low,mid]划分   MergeSort(arr,mid+1,high); //使用递归对arr[mid,high]划分   Merge(arr,low,mid,high); //对划分的有序小区域归并成一个有序区  } }