转载

剑指Offer面试题：13.调整数组顺序使奇数位于偶数前面

一、题目：调整数组顺序使奇数位于偶数前面

题目：输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。

例如有以下一个整数数组：12345，经过调整后可以为：15342、13542、13524等等。

二、解题思路

2.1 基本解法

如果不考虑时间复杂度，最简单的思路应该是从头扫描这个数组，每碰到一个偶数时，拿出这个数字，并把位于这个数字后面的所有数字往前挪动一位。挪完之后在数组的末尾有一个空位，这时把该偶数放入这个空位。由于每碰到一个偶数就需要移动O(n)个数字，因此总的时间复杂度是 O(n ² ) 。

2.2 高效解法

这里可以参考快速排序的思想，快速排序的基本思想是：通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序的目的。

剑指Offer面试题：13.调整数组顺序使奇数位于偶数前面

因此，我们可以借鉴快速排序的思想，通过设置两个指针来进行交换操作，从而减少移动次数，提高效率：

Step 1 . 第一个指针初始化时指向数组的第一个数字，它只向后移动；

Step 2 . 第二个指针初始化时指向数组的最后一个数字，它只向前移动。

Step 3 . 在两个指针相遇之前，第一个指针总是位于第二个指针的前面。如果第一个指针指向的数字是偶数，并且第二个指针指向的数字是奇数，我们就交换这两个数字。

下图展示了调整数组{1,2,3,4,5}使得奇数位于偶数前面的过程：

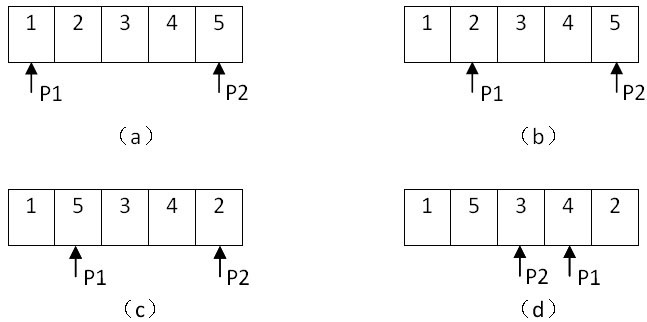
剑指Offer面试题：13.调整数组顺序使奇数位于偶数前面

三、解决问题

3.1 代码实现

（1）基本功能实现

public static void ReorderOddEven(int[] datas) {  if (datas == null || datas.Length <= 0)  {   return;  }  int begin = 0;  int end = datas.Length - 1;  int temp = -1;  while (begin < end)  {   // 向后移动begin，直到它指向偶数   while (begin < end && datas[begin] % 2 != 0)   {    begin++;   }   // 向前移动pEnd，直到它指向奇数   while (begin < end && datas[end] % 2 == 0)   {    end--;   }   if (begin < end)   {    // 交换偶数和奇数    temp = datas[begin];    datas[begin] = datas[end];    datas[end] = temp;   }  } }

怎么样，看起来是不是和快速排序的代码如出一辙？

（2）可扩展性实现

如果把题目改成把数组中的数按照大小分为两部分，所有负数都在非负数的前面，又或者改改，变成把数组中的数分为两部分，能被3整除的数都在不能被3整除的数的前面。面对需求的变化，我们发现代码变化的部分很小，因此从可扩展性的角度考虑，我们可以改写上面的代码如下，这里利用了.NET中的“函数指针”—委托来实现。

①方法实现

public static void ReorderOddEven(int[] datas, Predicate<int> func) {  if (datas == null || datas.Length <= 0)  {   return;  }  int begin = 0;  int end = datas.Length - 1;  int temp = -1;  while (begin < end)  {   // 向后移动begin，直到它指向偶数   while (begin < end && !func(datas[begin]))   {    begin++;   }   // 向前移动pEnd，直到它指向奇数   while (begin < end && func(datas[end]))   {    end--;   }   if (begin < end)   {    // 交换偶数和奇数    temp = datas[begin];    datas[begin] = datas[end];    datas[end] = temp;   }  } }

这里使用了.NET中的预定义委托Predicate，有不了解预定义委托的朋友可以阅读我另一篇博文：《 .NET中那些所谓的新语法之三》，这里就不再赘述了。

②如何调用

// 判断奇数还是偶数     ReorderHelper.ReorderOddEven(numbers, new Predicate<int>((num) => num % 2 == 0));     // 判断是能否被3整除     ReorderHelper.ReorderOddEven(numbers, new Predicate<int>((num) => num % 3 == 0));

这里使用了.NET中的Lambda表达式，同样，又不了解Lambda表达式的朋友也可以阅读我的另一篇博文：《 .NET中那些所谓的新语法之三》，这里也就不再赘述了。

3.2 单元测试

首先，这里封装了一个用于比较两个数组中的元素值是否相等的辅助方法：

// 辅助方法：对比两个数组是否一致 public bool ArrayEqual(int[] ordered, int[] expected) {  if (ordered.Length != expected.Length)  {   return false;  }  bool result = true;  for (int i = 0; i < ordered.Length; i++)  {   if (ordered[i] != expected[i])   {    result = false;    break;   }  }  return result; }

View Code

（1）功能测试

// Test1:输入数组中的奇数、偶数交替出现  [TestMethod]  public void ReorderTest1()  {   int[] numbers = { 1, 2, 3, 4, 5, 6, 7 };   int[] expected = { 1, 7, 3, 5, 4, 6, 2 };   ReorderHelper.ReorderOddEven(numbers);   Assert.AreEqual(ArrayEqual(numbers, expected), true);  }  // Test2:输入数组中的所有偶数都出现在奇数的前面  [TestMethod]  public void ReorderTest2()  {   int[] numbers = { 2, 4, 6, 1, 3, 5, 7 };   int[] expected = { 7, 5, 3, 1, 6, 4, 2 };   ReorderHelper.ReorderOddEven(numbers);   Assert.AreEqual(ArrayEqual(numbers, expected), true);  }  // Test3:输入数组中的所有奇数都出现在偶数的前面  [TestMethod]  public void ReorderTest3()  {   int[] numbers = { 1, 3, 5, 7, 2, 4, 6 };   int[] expected = { 1, 3, 5, 7, 2, 4, 6 };   ReorderHelper.ReorderOddEven(numbers);   Assert.AreEqual(ArrayEqual(numbers, expected), true);  }

（2）特殊输入测试

// Test4:输入的数组只包含一个数字-奇数  [TestMethod]  public void ReorderTest4()  {   int[] numbers = { 1 };   int[] expected = { 1 };   ReorderHelper.ReorderOddEven(numbers);   Assert.AreEqual(ArrayEqual(numbers, expected), true);  }  // Test5:输入的数组只包含一个数字-偶数  [TestMethod]  public void ReorderTest5()  {   int[] numbers = { 2 };   int[] expected = { 2 };   ReorderHelper.ReorderOddEven(numbers);   Assert.AreEqual(ArrayEqual(numbers, expected), true);  }  // Test6:NULL指针  [TestMethod]  public void ReorderTest6()  {   int[] numbers = null;   int[] expected = null;   ReorderHelper.ReorderOddEven(numbers);   Assert.AreEqual(numbers, expected);  }