转载

平衡二叉树插入与删除图文详解

一：平衡二叉树概念

花了很长时间，终于把平衡二叉树搞懂了，个人觉得这是初级数据结构里面比较难得一部分吧，比prim最小生成树，Dijkstra算法复杂多了。

因为平衡二叉树的提出是为了解决二叉搜索树的不平衡性导致的时间复杂度的不稳定，所以建议在搞懂二叉搜索树的前提下，再学习平衡二叉树。

二叉搜索树： http://ecizep.cn/a/shujujiegou/2015/0902/61.html

即在二叉搜索树的基础上，要保证每一步插入和删除操作之后保持二叉树的平衡。

我自己看数据结构书的时候，实在被书上的旋转给弄晕了，搞不懂结点怎么旋转的，更不用说每次旋转后的平衡因子的修改了。

所以到网上看了很多博客，其中有几篇写的很详细，根据那个思想才搞懂平衡二叉树。

先说基本概念，平衡二叉查找树，又称 AVL树。它除了具备二叉查找树的基本特征之外，还具有一个非常重要的特点：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值（平衡因子）不超过1。也就是说AVL树每个节点的平衡因子只可能是-1、0和1（左子树高度减去右子树高度）。

在插入和删除的基本操作上保持平衡的基本思想就是：

二：插入

插入算法很简单，和二叉搜索树一样，难的是一旦插入导致二叉树的不平衡，如何旋转结点并相应的修改平衡因子使之平衡。

而调整平衡则需要旋转：一共分为四种情况，左左，左右，右右，右左。每种情况分为二个图，图①为简单情况，图②为一般情况

(1)左左——LL

图①简单情况：在a的左孩子上插入一个结点y，导致x的平衡因子为2，旋转如图。

图②一般情况：在c的左孩子(或者右孩子，图②只画出左孩子情况，但是旋转操作一致)上插入一个结点y，导致x的平衡因子为2，x的lchild连上a的rchild,a的rchild连上x,完成旋转。

平衡二叉树插入与删除图文详解

void AdjustLL(AVL *T)//左左调整 {     AVL temp = (*T)->lchild;     (*T)->lchild = temp->rchild;     temp->rchild = (*T);     *T = temp; }

旋转后平衡因子变化：我们可以看到无论是哪种情况，只有x和a的平衡因子有所改变，且都变为0,。

即：x->bf = 0,a->bf =0。（bf为每个结点的平衡因子）

子树高度变化：可以看到插入前后插入后高度没有发生变化，图①插入前高度为2，插入调整平衡后高度还是2，图②插入前后高度都是3.

即：左左旋转子树高度不变化。

(注：之所以要观察旋转后的高度变化是为了在递归回溯时，方便根据不同情况来修改父元素结点的平衡因子，因为x可能是某个结点的孩子结点，x的高度改变必然引起父元素平衡因子改变)

(2)右右——RR

图①简单情况：在a的右孩子上插入一个结点y，导致x的平衡因子为-2，旋转如图。

图②一般情况：在c的右孩子(或者左孩子，图②只画出右孩子情况，但是旋转操作一致)上插入一个结点y，导致x的平衡因子为-2，x的rchild连上a的lchild,a的lchild连上x,完成旋转。

平衡二叉树插入与删除图文详解

void AdjustRR(AVL *T)//右右调整    {     AVL temp = (*T)->rchild;     (*T)->rchild = temp->lchild;     temp->lchild = (*T);     (*T) = temp; }

旋转后平衡因子变化：我们可以看到无论是哪种情况，只有x和a的平衡因子有所改变，且都变为0,。

即：x->bf = 0,a->bf =0。

子树高度变化：右右旋转，子树插入结点前后高度不变化。

(3)左右——LR

图①简单情况：在a的右孩子结点上插入一个结点y,x失去平衡，旋转分两步：1.以a为根结点的RR旋转 2.以x为根结点的LL旋转。

图②一般情况：在c的右孩子结点（或者左孩子）插入一个结点y,x失去平衡，同样分为两步：1.以a为根节点的RR旋转 2.以X为根结点的LL旋转。

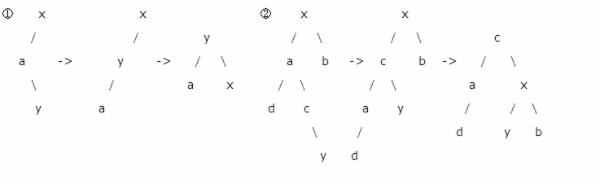
平衡二叉树插入与删除图文详解

LR旋转的实现:

1.可以通过调用RR(a)和LL(x)实现,

2.我们可以将LR看做一步变换得来,即a的rchild连上c的lchild，c的lchild连接上a,x的lchild连接上c的rchild,c的rchild连接上x。

void AdjustLR(AVL *T)//左右调整 {  AVL p1,p2;  p1 = (*T)->lchild;  p2 = p1->rchild;  p1->rchild = p2->lchild;//p2左孩子连上p1的右孩子  (*T)->lchild = p2->rchild;//p2右孩子连上(*T)的左孩子  p2->lchild = p1;  p2->rchild = (*T);  (*T) = p2; }

旋转后平衡因子变化：

(1)当c->bf = 1时，a->bf = 0,x->bf = -1;

(2)当c->bf = -1时，a->bf = 1,x->bf = 0;

(3)当c点就是插入结点y时(图①简单情况)，a->bf = x->bf =0;

子树高度变化：左右旋转，子树结点插入前后高度不变化。

(4)右左——RL

图①简单情况：在a的左孩子结点上插入一个结点y,x失去平衡，旋转分两步：1.以a为根结点的LL旋转 2.以x为根结点的RR旋转。

图②一般情况：在c的右孩子结点（或者左孩子）插入一个结点y,x失去平衡，同样分为两步：1.以a为根节点的LL旋转 2.以X为根结点的RR旋转。

平衡二叉树插入与删除图文详解

RL旋转的实现:

1.可以通过调用LL(a)和RR(x)实现,

2.我们可以将RL看做一步变换得来,即a的lchild连上c的rchild，c的rchild连接上a,x的rchild连接上c的lchild,c的lchild连接上x。

void AdjustRL(AVL *T)//右左调整   {  AVL p1,p2;  p1 = (*T)->rchild;  p2 = p1->lchild;  (*T)->rchild = p2->lchild;  p1->lchild = p2->rchild;  p2->lchild = (*T);  p2->rchild = p1;  (*T) = p2; }

旋转后平衡因子变化：

(1)当c->bf = 1时，a->bf = -1,x->bf = 0;

(2)当c->bf = -1时，a->bf = 0,x->bf = 1;

(3)当c点就是插入结点y时(图①简单情况)，a->bf = x->bf =0;

子树高度变化：右左旋转，子树结点插入前后高度不变化。

以上就是旋转的所有情况以及旋转前后平衡因子变化，可以看到凡是插入结点后，导致了不平衡而旋转调整，则子树高度不变化，根节点向上的父元素的因子不用修改。

那如果插入后没有引起不平衡，相应的平衡因子应该做如何修改呢？实际上，就是子树上含新结点的结点因子相应的+1或者-1，但是一种特殊情况要注意，就是当插入结点后，结点平衡因子变为0的结点（插入前平衡因子为1或者-1），其子树高度也没有改变，则从此结点开始向上的父结点元素因子无需改变。

特殊情况图：

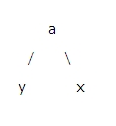平衡二叉树插入与删除图文详解插入y或者x，a的高度没有变化，父元素结点平衡因子不用修改。

插入及平衡调整：

void LeftBanlance(AVL *T)// 左平衡处理：LL LR 情况 {  AVL lc = (*T)->lchild,rc;  switch(lc->bf)  {   case 1: //LL情况    (*T)->bf = 0;    lc->bf = 0;    AdjustLL(T);    break;   case 0:    //删除时需要，插入不需要    (*T)->bf = 1;    lc->bf = -1;    AdjustLL(T);    break;   case -1: //LR情况    rc = lc->rchild;    switch(rc->bf)    {     case 1:      (*T)->bf = -1;      lc->bf = 0;      break;     case 0:      (*T)->bf = 0;      lc->bf = 0;      break;     case -1:      (*T)->bf = 0;      lc->bf = 1;      break;    }    rc->bf = 0;    AdjustLR(T);    break;  } } void RightBanlance(AVL *T)//右平衡处理：RR RL情况 {  AVL rc = (*T)->rchild,lc;  switch(rc->bf)  {   case -1:    (*T)->bf  = 0;    rc->bf = 0;    AdjustRR(T);    break;   case 0:   //删除时需要，插入不需要    (*T)->bf = -1;    rc->bf = 1;    AdjustRR(T);    break;   case 1:    lc = rc->lchild;    switch(lc->bf)    {     case 1:      (*T)->bf = 0;      rc->bf = -1;      break;     case 0:      (*T)->bf = 0;      rc->bf = 0;      break;     case -1:      (*T)->bf = 1;      rc->bf = 0;      break;    }    lc->bf = 0;    AdjustRL(T);    break;  } } int Insert(AVL *T,data_type data,int *taller)//插入 {  AVL newnode,p;  newnode = (AVL)malloc(sizeof(AVLNode));  newnode->lchild = NULL;  newnode->rchild = NULL;  newnode->data = data;  newnode->bf = 0;  if((*T) == NULL) //插入成功，子树变高  {   (*T) = newnode;   *taller = 1;  }  else  {   if(data == (*T)->data)//数据已存在，不插入   {    *taller = 0;    return 0;   }   else if(data < (*T)->data)//左子树中查找   {    if(Insert(&(*T)->lchild,data,taller) == 0)//插入失败    {     return 0;    }    if((*taller) == 1)  //插入成功且子树变高，对bf做相应修改以及平衡调整    {     switch((*T)->bf)     {      case 1:       LeftBanlance(T); //处理左平衡，插入操作平衡处理完，子树高度不变       *taller = 0;       break;      case 0:       (*T)->bf = 1;       *taller = 1;       break;      case -1:       (*T)->bf = 0;       *taller = 0;       break;     }    }   }   else//右子树中查找   {    if(Insert(&(*T)->rchild,data,taller) == 0)//插入失败    {     return 0;    }    if((*taller) == 1)    {     switch((*T)->bf)     {      case 1:       (*T)->bf = 0;       *taller = 0;       break;      case 0:       (*T)->bf = -1;       *taller = 1;       break;      case -1:       RightBanlance(T);       *taller = 0;       break;     }    }   }  }  return 1; }

三：删除

此处不在对删除结点的思路进行讲解，只讨论删除结点后平衡因子的变化以及旋转调整平衡。

对结点删除算法还不了解的，请看我的上一篇博客二叉搜索树，里面有详细讲解： http://ecizep.cn/a/shujujiegou/2015/0902/61.html

插入结点后导致不平衡有4种情况，而删除结点后导致不平衡有6种情况，左子树3种，右子树3种，不过左右对称，原理是一样的，所以这里我只列出右子树的三种情况。

图片引用来至： http://blog.csdn.net/goodluckwhh/article/details/11786079

(1)失衡结点的右子树的平衡因子为-1

该情形如下图所示：

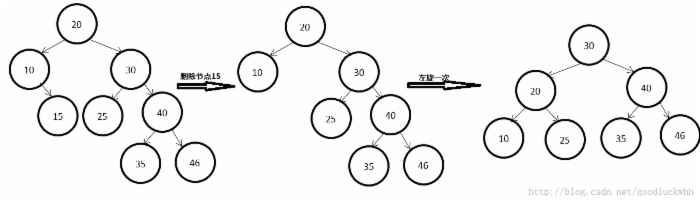
平衡二叉树插入与删除图文详解

该情形很简单，就是以A(20)为根结点做一次RR旋转处理。

平衡因子变化：A以及A的右子树bf都变为0，其他结点不变化。

子树高度降低，即A的父元素结点平衡因子需做修改。

(2)失衡结点的右子树的平衡因子为0

该情形如下图所示：

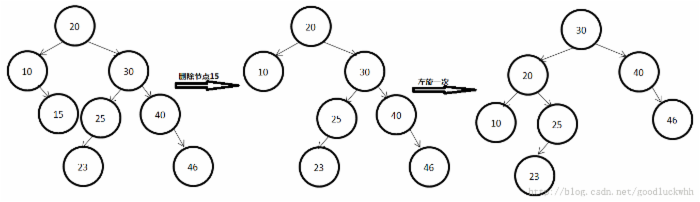
平衡二叉树插入与删除图文详解

同样是以A（20）为根结点做RR旋转。

平衡因子变化：A的平衡因子变为-1，A的右孩子结点平衡因子为1，其他不变化。

子树高度没有降低，即A的父元素结点平衡因子不需做修改。

(3)失衡结点的右子树的平衡因子为1

该情形如下图：

平衡二叉树插入与删除图文详解

该情况就和插入时RL的情况一致，不在赘述，调用RL旋转函数就可以了。

但是平衡因子变化和插入不同：A（20）和A的右孩子结点平衡因子都为0.

子树高度降低，即A的父元素结点平衡因子要修改。

以上即为右子树（删除结点在左子树）的三种情况，左子树三种情况类似。

如果删除后，无需做旋转调整平衡，则删除结点查找路径上的结点平衡因子相应的-1或者+1，也有一种特殊情况，和插入相反，即删除前结点平衡因子为0的结点，子树高度不降低，父元素因子不用修改。

特殊情况如图：

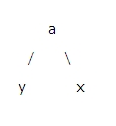平衡二叉树插入与删除图文详解删除y或者x，a的高度不变化。

删除及平衡调整：

/* 若等于，则删除,并且高度降低，在递归回溯时对父元素bf做相应修改 若小于，向左边递归，若大于，向右边递归 只有当删除成功，且树高度降低时，做bf相应修改，否则结束函数。*/ int Delete(AVL *T,data_type data,int *shorter)//删除 {  if((*T) == NULL)  {   return 0;  }  else if(data == (*T)->data)  //删除  此处删除算法原理同二叉搜索树  {   AVL temp = (*T);   if((*T)->lchild == NULL)   {    (*T) = (*T)->rchild;    free(temp);    *shorter = 1;   }   else if((*T)->rchild == NULL)   {    (*T) = (*T)->lchild;    free(temp);    *shorter = 1;   }   else   {    AVL p = (*T)->lchild;    while(p->rchild)    {     p = p->rchild;    }    temp->data = p->data;    Delete(&(temp->lchild),p->data,shorter);   }  }  else if(data < (*T)->data)  //左子树中继续查找  {   if(!Delete(&((*T)->lchild),data,shorter))//删除失败直接return 0   {    return 0;   }   if(*shorter) //左子树中结点删除成功,并且子树高度降低   {    switch((*T)->bf)    {     case 1:      (*T)->bf = 0;      *shorter = 1;      break;     case 0:    //子树高度不降低的特殊情况:即左右都有结点，删除一个不影响子树高度      (*T)->bf = -1;      *shorter = 0;      break;     case -1:      if((*T)->rchild->bf == 0)//删除时的特殊情况：右孩子结点bf为0，子树高度不变      {       *shorter = 0;      }      else      {       *shorter = 1;      }      RightBanlance(T);  //处理右平衡      break;    }   }  }  else    //右子树中继续查找  {   if(!Delete(&(*T)->rchild,data,shorter))   {    return 0;   }   if(*shorter)    {    switch((*T)->bf)    {     case 1:      if((*T)->lchild->bf == 0)      {       *shorter = 0;      }      else      {       *shorter = 1;      }      LeftBanlance(T);      break;     case 0:      (*T)->bf = 1;      *shorter = 0;      break;     case -1:      (*T)->bf = 0;      *shorter = 1;      break;    }   }  }  return 1; }