机器学习(九)—FP-growth算法
本来老师是想让我学Hadoop的,也装了Ubuntu,配置了Hadoop,一时间却不知从何学起,加之自己还是想先看点自己喜欢的算法,学习Hadoop也就暂且搁置了,不过还是想问一下园子里的朋友有什么学习Hadoop好点的资料,求推荐~言归正传,继Apriori算法之后,今天来学习FP-growth算法。
和Apriori算法相比,FP-growth算法只需要对数据库进行两次遍历,从而高效发现频繁项集。对于搜索引擎公司而言,他们需要通过查看互联网上的用词来找出经常在一块出现的词对,因此这些公司就需要能够高效的发现频繁项集的方法,今天要学习的FP-growth算法就可以完成此重任。
一 FP-growth算法
1.概述
FP-growth算法是基于Apriori原理的,通过将数据集存储在FP(Frequent Pattern)树上发现频繁项集,但不能发现数据之间的关联规则。FP-growth算法只需要对数据库进行两次扫描,而Apriori算法在求每个潜在的频繁项集时都需要扫描一次数据集,所以说Apriori算法是高效的。其中算法发现频繁项集的过程是:
(1)构建FP树;
(2)从FP树中挖掘频繁项集。
2. 构建FP树
FP表示的是频繁模式,其通过链接来连接相似元素,被连起来的元素可以看成是一个链表。将事务数据表中的各个事务对应的数据项按照支持度排序后,把每个事务中的数据项按降序依次插入到一棵以 NULL为根节点的树中,同时在每个结点处记录该结点出现的支持度。
FP-growth算法的流程为:首先构造FP树,然后利用它来挖掘频繁项集。在构造FP树时,需要对数据集扫描两边,第一遍扫描用来统计频率,第二遍扫描至考虑频繁项集。下面举例对FP树加以说明。
假设存在的一个事务数据样例为,构建FP树的步骤如下:
| 事务ID | 事务中的元素 |
| 001 | r,z,h,j,p |
| 002 | z,y,x,w,v,u,t,s |
| 003 | z |
| 004 | r,x,n,o,s |
| 005 | y,r,x,z,q,t,p |
| 006 | y,z,x,e,q,s,t,m |
结合Apriori算法中最小支持度的阈值,在此将最小支持度定义为3,结合上表中的数据,那些不满足最小支持度要求的将不会出现在最后的FP树中,据此构建FP树,并采用一个头指针表来指向给定类型的第一个实例,快速访问FP树中的所有元素,构建的带头指针的FP树如下:

结合绘制的带头指针表的FP树,对表中数据进行过滤,排序如下:
| 事务ID | 事务中的元素 | 过滤和重排序后的事务 |
| 001 | r,z,h,j,p | z,r |
| 002 | z,y,x,w,v,u,t,s | z,x,y,s,t |
| 003 | z | z |
| 004 | r,x,n,o,s | x,s,r |
| 005 | y,r,x,z,q,t,p | z,x,y,r,t |
| 006 | y,z,x,e,q,s,t,m | z,x,y,s,t |
在对数据项过滤排序了之后,就可以构建FP树了,从NULL开始,向其中不断添加过滤排序后的频繁项集。过程可表示为:
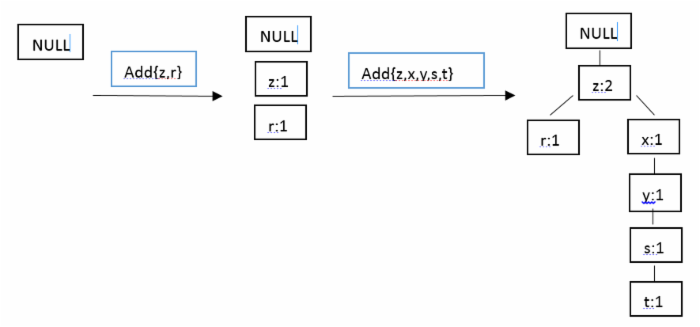
根据该思想就可以实现FP树的构建,下面就采用Python进行实现。我们知道, 在第二次扫描数据集时会构建一棵FP树,并采用一个容器来保存树。首先创建一个类来保存树的每一个节点,代码如下:
#coding:utf-8 from numpy import * class treeNode: def __init__(self, nameValue, numOccur, parentNode): self.name = nameValue self.count = numOccur self.nodeLink = None self.parent = parentNode #needs to be updated self.children = {} def inc(self,numOccur): self.count += numOccur def disp(self,ind = 1): print ' '*ind,self.name,' ',self.count for child in self.children.values(): child.disp(ind+1) ''' #test rootNode = treeNode('pyramid',9,None) rootNode.children['eye'] = treeNode('eye',13,None) a = rootNode.disp() print a ''' 这样,FP树对应的数据结构就建好了,现在就可以构建FP树了,FP树的构建函数如下:
#FP构建函数 def createTree(dataSet,minSup = 1): headerTable = {} for trans in dataSet: for item in trans: headerTable[item] = headerTable.get(item,0) + dataSet[trans]#记录每个元素项出现的频度 for k in headerTable.keys(): if headerTable[k] < minSup: del(headerTable[k]) freqItemSet = set(headerTable.keys()) if len(freqItemSet) == 0:#不满足最小值支持度要求的除去 return None,None for k in headerTable: headerTable[k] = [headerTable[k],None] retTree = treeNode('Null Set',1,None) for tranSet,count in dataSet.items(): localD = {} for item in tranSet: if item in freqItemSet: localD[item] = headerTable[item][0] if len(localD) > 0: orderedItems = [v[0] for v in sorted(localD.items(),key = lambda p:p[1],reverse = True)] updateTree(orderedItems,retTree,headerTable,count) return retTree,headerTable def updateTree(items, inTree, headerTable, count): if items[0] in inTree.children: inTree.children[items[0]].inc(count) else: inTree.children[items[0]] = treeNode(items[0], count, inTree) if headerTable[items[0]][1] == None: headerTable[items[0]][1] = inTree.children[items[0]] else: updateHeader(headerTable[items[0]][1], inTree.children[items[0]]) if len(items) > 1: updateTree(items[1::], inTree.children[items[0]], headerTable, count) def updateHeader(nodeToTest, targetNode): while (nodeToTest.nodeLink != None): nodeToTest = nodeToTest.nodeLink nodeToTest.nodeLink = targetNode 在运行上例之前还需要一个真正的数据集,结合之前的数据自定义数据集:
def loadSimpDat(): simpDat = [['r', 'z', 'h', 'j', 'p'], ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'], ['z'], ['r', 'x', 'n', 'o', 's'], ['y', 'r', 'x', 'z', 'q', 't', 'p'], ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']] return simpDat def createInitSet(dataSet): retDict = {} for trans in dataSet: retDict[frozenset(trans)] = 1 return retDict 运行:
#test simpDat = loadSimpDat() initSet = createInitSet(simpDat) myFPtree,myHeaderTab = createTree(initSet,3) a = myFPtree.disp() print a 这样就构建了FP树,接下来就是使用它来进行频繁项集的挖掘。
3. 从FP树中挖掘频繁项集
在构建了FP树之后,就可以抽取频繁项集了,这里的思想和Apriori算法大致类似,首先从氮元素项集合开始,然后在此基础上逐步构建更大的集合。大致分为三个步骤:
(1)从FP树中获得条件模式基;
(2)利用条件模式基,构建一个条件FP树;
(3)迭代重复(1)和(2),直到树包含一个元素项为止。
首先,获取条件模式基。条件模式基是以所查找元素项为结尾的路径集合,表示的是所查找的元素项与树根节点之间的所有内容。结合构建FP树绘制的图,r的前缀路径就是{x,s}、{z,x,y}和{z},其中的每条前缀路径都与一个计数值有关,该计数值表示的是每条路径上r的数目。为了得到这些前缀路径,结合之前所得到的头指针表,头指针表中包含相同类型元素链表的起始指针,根据每一个元素项都可以上溯到这棵树直到根节点为止。该过程对应的代码如下:
def ascendTree(leafNode, prefixPath): #ascends from leaf node to root if leafNode.parent != None: prefixPath.append(leafNode.name) ascendTree(leafNode.parent, prefixPath) def findPrefixPath(basePat, treeNode): #treeNode comes from header table condPats = {} while treeNode != None: prefixPath = [] ascendTree(treeNode, prefixPath) if len(prefixPath) > 1: condPats[frozenset(prefixPath[1:])] = treeNode.count treeNode = treeNode.nodeLink return condPats #test simpDat = loadSimpDat() initSet = createInitSet(simpDat) myFPtree,myHeaderTab = createTree(initSet,3) a = myFPtree.disp() b = findPrefixPath('x',myHeaderTab['x'][1]) print b 运行代码,与所给数据一致。接下来就可以创建条件FP树了。对于每一个频繁项,都需要创建一棵条件FP树,使用刚才创建的条件模式基作为输入,采用相同的建树代码来构建树,相应的递归发现频繁项、发现条件模式基和另外的条件树。对应的递归查找频繁项集的函数如下:
def mineTree(inTree, headerTable, minSup, preFix, freqItemList): bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1])]#(sort header table) for basePat in bigL: newFreqSet = preFix.copy() newFreqSet.add(basePat) freqItemList.append(newFreqSet) condPattBases = findPrefixPath(basePat, headerTable[basePat][1]) myCondTree, myHead = createTree(condPattBases, minSup) if myHead != None: mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList) 结合之前的数据验证发现无误。
二 从新闻网站点击流中挖掘
上述在自定义的数据中队算法进行了验证,现在选取实际的数据进行测试。在这个数据集合中,包含了100万条记录,文件中的每一行包含某个用户浏览过的新闻报道,用来寻找那些至少被10万人浏览过的报道。代码如下:
#从新闻网站点击流中挖掘 parsedData = [line.split() for line in open('kosarak.dat').readlines()] initSet = createInitSet(parsedData) myFPtree,myHeaderTab = createTree(initSet,100000) myFreqList = [] a = mineTree(myFPtree,myHeaderTab,100000,set([]),myFreqList) b = len(myFreqList) print b print myFreqList 这样就实现了此功能。
以上是我自己的总结和理解,难免有错,还望各位朋友不吝赐教~











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

