统计学习方法之决策树（2）信息增益比，决策树的生成算法
声明：原创内容，如需转载请注明出处
今天讲解的内容是：
信息增益比，决策树的生成算法—ID3和C4.5
我们昨天已经学习了什么是信息增益，并且通过信息增益来选择最优特征，但是用信息增益会出现偏向于选择取值多的特征。
来解释下这句话。以最极端的情况举例，比如有6个样本，特征年龄的取值为5个值，19岁，20岁，21岁，22岁，23岁。
假设19岁的贷款情况为“是”，20岁为“否”，21岁“是”，22岁“否”，23岁“是”。
那么来一个新的申请者20岁，那么直接分类为“否”。这显然是不合理的。
这样的分类结果是确定的。 也就是说经验条件熵为0（括号里的）。这意味着该情况下的信息增益达到了最大值。
所以取值更多的属性，更容易使得数据更“纯”（尤其是连续型数值），其信息增益更大，决策树会首先挑选这个属性作为树的顶点。结果训练出来的形状是一棵庞大且深度很浅的树，这样的划分是极为不合理的。
在此引入了 信息增益比
信息增益比是信息增益和训练数据D关于特征A的熵H(D)
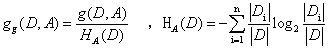
也叫做拆分信息，这个特征取得值越多（拆分的越多）熵H(D)越大，g(D,A)也越大，算出来的熵就会被综合。用信息增益比来选取特征就会更准确一点。
决策树的生成算法C4.5就是使用了信息增益率，在信息增益的基础上除了一项split information（拆分信息）,来惩罚值更多的属性。
另一个决策树的生成算法是ID3算法，是以信息增益为准则选取特征。
ID3算法
从根节点开始，计算所有可能的特征的信息增益，选择信息增益最大的特征作为当前节点的特征，由特征的不同取值建立空白子节点，对空白子节点递归调用此方法，直到所有特征的信息增益小于阀值或者没有特征可选为止。
在昨天讲过的这个例子中，由于有房子的信息增益最大，所以选择它作为根节点。它将训练数据D分为两个子集D1，D2，D1取“是”，D2取“否”，由于D1里的数据是同一类样本点（就是在下图表中，有房子的（“是”）项，对应的最后一列的类别都是（“是”）所以不需要对这个节点在进行操作，它就成为了叶节点。
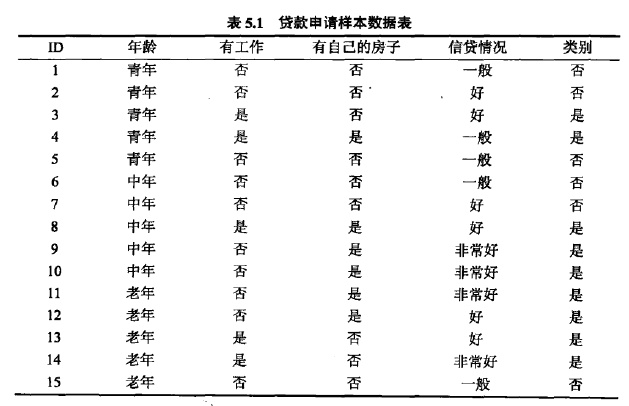
由于D2里的数据不都是属于同一类别。则要通过ID3算法，从其他的特征中选出一个来作为新特征。通过计算选取的是“有工作”
最后就生成了这样一棵树。
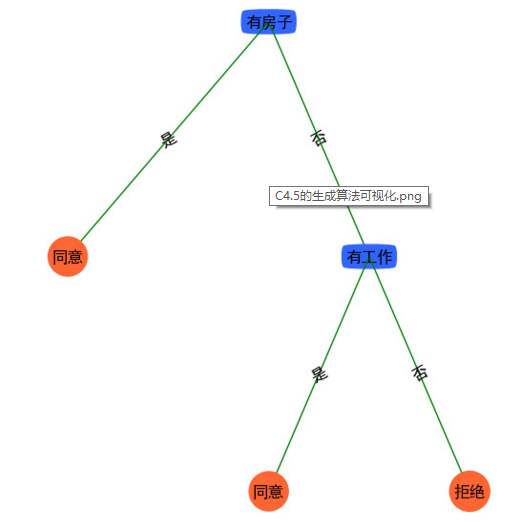
而 C4.5 只是把其中的信息增益换成信息增益比 ，其他的就没有区别了。
由于决策生成算法（ID3，C4.5）容易产生过拟合，在学习的过程中过多的考虑对训练数据的正确分类，从而构建出过于复杂的树。
在下一次中，我们将学习，如何对这样的树做出简化。
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
