CTF：HITB 2015 加密解密部分Write-up

介绍

加密类300分这道挑战题目是有关于RSA生成的质数p和q。我们现目前获得了一份RSA加密过的邮件mail.msg，以及隐藏有公钥的证书hitbctf.crt。所有文件会在文尾分享！

RSA参数结构

模N是由第一个质数P随机选择，第二个质数是由以下方式构成：

k是一个正整数，q是一个质数，e是一个公用的指数且还是一个质数。

下面的代码是由Python实现：

def gen_rsa_parameters():     r = os.urandom(63)     e = int(r.encode('hex'), 16)     e = next_prime(e)     r = os.urandom(64)     p = int(r.encode('hex'), 16)     p = next_prime(p)     q = (p*modinv(p-1, e)%e)         while not is_prime(q):         q += e     N = p*q     phi = (p-1)*(q-1)     d = modinv(e,phi)         return N,e,d,p,q

攻击假想

令N′=N mod e，我们可以得到：

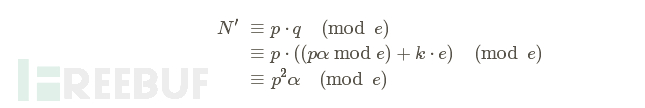
由于方程中存在α，所以我们引入p−1来替换

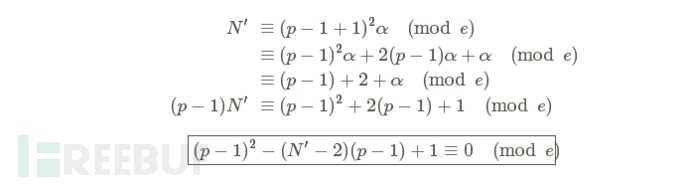
现在我们获得了一个取决于p的二次方程。

令X = p−1并假设N′−2位偶数且N′−2 = 2b

通过使用二次剩余[ 百度百科 , 维基百科中文 , 维基百科英文 ]，我们确定并找到了解决方案。我们还可以使用SAGE以及sqrt()函数：

Np = N % e b = (Np - 2) / 2 p = Mod(pow(b, 2) - 1, e).sqrt() + b + 1

我们获得的是p mod e而不是p！

我尝试增加一些次方来找到p，但是p和 p mod e之间的距离实在太大了。

所以我们必须放弃这条道，选择另外的方法了。

通过了解p mod e我们还可以计算α

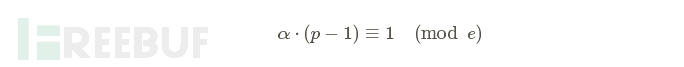
拥有了α和p mod e我们就可以通过递增e直到(pα mod e)+k⋅e为质数且能整除N。

我们假设N′−2为偶数(所以N′必须是偶数)，如果在证书中N′为偶数那么这一切猜想也就成立了。

实际攻击

首先我们从证书中提取模N和公钥e：

openssl x509 -in hitbctf.crt -text -noout Certificate:   Data:     Version: 1 (0x0)     Serial Number: 18379438180976429416 (0xff10e1a5ac5a0968)   Signature Algorithm: sha1WithRSAEncryption     Issuer: C=NL, ST=Noord-Holland, L=Amsterdam, O=HITB, OU=CTF     Validity    Not Before: May 24 09:58:26 2015 GMT       Not After : May 23 09:58:26 2016 GMT       Subject: C=NL, ST=Noord-Holland, L=Amsterdam, O=HITB, OU=CTF       Subject Public Key Info:       Public Key Algorithm: rsaEncryption         Public-Key: (1024 bit)         Modulus:           00:e6:eb:89:c1:8d:49:c9:a2:02:2b:e0:b4:65:14:           6e:0f:90:45:1e:a3:4c:6b:60:56:00:4e:bd:15:59:         55:b1:35:96:c2:d6:83:ad:2f:23:6b:0b:2c:0e:0b:         88:83:b5:d6:cb:8a:0b:4f:f9:b7:eb:64:8c:95:2b:         6b:ef:5a:6f:04:f5:64:17:f5:1c:a9:14:d9:ea:73:         e7:dd:c5:f2:0d:ce:c3:9c:e8:4b:72:2a:0c:f3:d8:         5e:80:ce:78:64:63:e1:44:f6:1d:b5:9c:cf:45:ff:         0e:d3:7f:d0:ce:bd:37:a5:8d:8a:4b:08:33:9e:a3:         2c:bc:ab:61:64:03:fd:2c:c5         Exponent:           69:60:2d:93:8a:81:5f:14:cf:9f:b8:36:c2:e0:4d:           4d:de:82:ba:fc:8d:56:c2:6d:8c:89:ef:3c:40:69:         5d:d5:d4:ef:a7:36:36:43:15:14:95:f3:8c:bf:24:         ae:94:30:92:40:79:12:00:1b:17:f5:53:33:9e:92:         70:70:49   Signature Algorithm: sha1WithRSAEncryption     17:2b:ea:be:90:ad:98:f2:2b:ff:f5:61:d3:ea:af:fb:35:3a:     67:10:91:13:db:60:55:d9:09:8b:c2:1a:cf:6b:c6:1f:f2:10:     7a:d1:7b:9d:ff:10:f2:f2:c0:a9:f5:aa:2e:09:93:40:88:92:     7d:98:ff:e1:cb:dc:db:35:8d:e0:4b:21:99:76:bf:db:04:a2:     62:a4:18:4e:fc:bb:a7:53:be:6a:a1:ef:ec:15:86:c1:f1:1e:     87:6a:e9:af:fe:d1:08:eb:de:22:28:c4:5e:be:f1:41:0a:ca:     cf:cf:da:63:b1:c1:56:e8:0c:8e:56:7f:08:94:0d:2b:2a:08: 

N = 162157588231432175750266419709084494256738149198416702818838192688585199555839792754739411546929869488574731499231574687207152393171517768019327338646577588312972543620665360591059281057979460340279244616489314862289312195704820435867259965443285749719682327313893490163672147378911558526315013166594183212229

e = 215584882345398898379387706359713309034898391467668952244901790414655161931455822669631548838317075220811407344210520390992334648372016602816069805 30249

SAGE:

sage: Np = N % e sage: b = (Np - 2) / 2sage: pp = int(Mod(pow(b, 2) - 1, e).sqrt()) + b + 1sage: alpha = inverse_mod(int(X), int(e)) sage: q = (pp * alpha) % e sage: while not is_prime(q) and N % q != 0: ....:         q += e sage: p = N / q sage: p13317713478157317654574552532079837937895228108820477140030796245493222349714497856652987583926206280627498615972491072112647669795345566943409669535038641sage: q12176083266650126897170100375931110708350668494730113414987801764299563774952801449439933220072280766145748279998832962142839152786620322097065894585706069

rsatool.py：

#!/usr/bin/env python2 import base64, fractions, optparse, random import gmpy from pyasn1.codec.der import encoder from pyasn1.type.univ import * PEM_TEMPLATE = '-----BEGIN RSA PRIVATE KEY-----/n%s-----END RSA PRIVATE KEY-----/n' DEFAULT_EXP = 65537 def factor_modulus(n, d, e):  """  Efficiently recover non-trivial factors of n  See: Handbook of Applied Cryptography  8.2.2 Security of RSA -> (i) Relation to factoring (p.287)  http://www.cacr.math.uwaterloo.ca/hac/  """  t = (e * d - 1)  s = 0  while True:   quotient, remainder = divmod(t, 2)   if remainder != 0:    break   s += 1   t = quotient  found = False  while not found:   i = 1   a = random.randint(1,n-1)   while i <= s and not found:    c1 = pow(a, pow(2, i-1, n) * t, n)    c2 = pow(a, pow(2, i, n) * t, n)    found = c1 != 1 and c1 != (-1 % n) and c2 == 1    i += 1  p = fractions.gcd(c1-1, n)  q = (n / p)  return p, q class RSA:  def __init__(self, p=None, q=None, n=None, d=None, e=DEFAULT_EXP):   """   Initialize RSA instance using primes (p, q)   or modulus and private exponent (n, d)   """   self.e = e   if p and q:    assert gmpy.is_prime(p), 'p is not prime'    assert gmpy.is_prime(q), 'q is not prime'    self.p = p    self.q = q   elif n and d:       self.p, self.q = factor_modulus(n, d, e)   else:    raise ArgumentError('Either (p, q) or (n, d) must be provided')   self._calc_values()  def _calc_values(self):   self.n = self.p * self.q   phi = (self.p - 1) * (self.q - 1)   self.d = gmpy.invert(self.e, phi)   # CRT-RSA precomputation   self.dP = self.d % (self.p - 1)   self.dQ = self.d % (self.q - 1)   self.qInv = gmpy.invert(self.q, self.p)  def to_pem(self):   """   Return OpenSSL-compatible PEM encoded key   """   return PEM_TEMPLATE % base64.encodestring(self.to_der())  def to_der(self):   """   Return parameters as OpenSSL compatible DER encoded key   """   seq = Sequence()   for x in [0, self.n, self.e, self.d, self.p, self.q, self.dP, self.dQ, self.qInv]:    seq.setComponentByPosition(len(seq), Integer(x))   return encoder.encode(seq)  def dump(self, verbose):   vars = ['n', 'e', 'd', 'p', 'q']   if verbose:    vars += ['dP', 'dQ', 'qInv']   for v in vars:    self._dumpvar(v)  def _dumpvar(self, var):   val = getattr(self, var)   parts = lambda s, l: '/n'.join([s[i:i+l] for i in xrange(0, len(s), l)])   if len(str(val)) <= 40:    print '%s = %d (%#x)/n' % (var, val, val)   else:    print '%s =' % var    print parts('%x' % val, 80) + '/n' if __name__ == '__main__':  parser = optparse.OptionParser()  parser.add_option('-p', dest='p', help='prime', type='int')  parser.add_option('-q', dest='q', help='prime', type='int')  parser.add_option('-n', dest='n', help='modulus', type='int')  parser.add_option('-d', dest='d', help='private exponent', type='int')  parser.add_option('-e', dest='e', help='public exponent (default: %d)' % DEFAULT_EXP, type='int', default=DEFAULT_EXP)  parser.add_option('-o', dest='filename', help='output filename')  parser.add_option('-f', dest='format', help='output format (DER, PEM) (default: PEM)', type='choice', choices=['DER', 'PEM'], default='PEM')  parser.add_option('-v', dest='verbose', help='also display CRT-RSA representation', action='store_true', default=False)  try:   (options, args) = parser.parse_args()   if options.p and options.q:    print 'Using (p, q) to initialise RSA instance/n'    rsa = RSA(p=options.p, q=options.q, e=options.e)   elif options.n and options.d:    print 'Using (n, d) to initialise RSA instance/n'    rsa = RSA(n=options.n, d=options.d, e=options.e)   else:    parser.print_help()    parser.error('Either (p, q) or (n, d) needs to be specified')   rsa.dump(options.verbose)   if options.filename:    print 'Saving %s as %s' % (options.format, options.filename)    if options.format == 'PEM':     data = rsa.to_pem()    elif options.format == 'DER':     data = rsa.to_der()    fp = open(options.filename, 'wb')    fp.write(data)    fp.close()  except optparse.OptionValueError, e:   parser.print_help()   parser.error(e.msg) 

接着使用rsatool.py生成一个私钥：

$ ./rsatools.py -o private.pem / -e 21558488234539889837938770635971330903489839146766895224490179041465516193145582266963154883831707522081140734421052039099233464837201660281606980530249 / -p 13317713478157317654574552532079837937895228108820477140030796245493222349714497856652987583926206280627498615972491072112647669795345566943409669535038641 / -q 12176083266650126897170100375931110708350668494730113414987801764299563774952801449439933220072280766145748279998832962142839152786620322097065894585706069

然后解密信息：

openssl smime -decrypt -in mail.msg -inkey private.pem hitb{0b21cc2025534dbd2965390d2bcef45d}

链接： http://pan.baidu.com/s/1kTAjeHT 密码：iy4v

* 参考来源： RomainThomas ，编译/FB小编鸢尾，转载请注明来自FreeBuf黑客与极客（FreeBuf.COM）