转载

OPEN CASCADE Curve Continuity

eryar@163.com

Abstract.设计一条复杂曲线时，出于设计和制造上的考虑，常常通过多段曲线组合而成，这就需要解决曲线段之间如何实现光滑连接的问题。评价曲线间连接的光滑度的度量有两种：参数连接性和几何连续性。本文对这两种连续性分别进行介绍。

Key Words.Curve Continuity, Geometric Continuity, 参数连续性、几何连续性

1.Introduction

在实际应用中进行复杂零件的几何设计时，通常我们用到的不仅仅是整个曲线，而是满足一定的连续条件拼接而成的曲线段组成的组合曲线。关于连续条件有两种不同的度量方法。一种是满足于数学上严格定义的函数曲线可微性方法；别一种是满足相对宽松的约束条件的几何连续性方法。

本文对连续性的两种度量方法进行介绍，来理解参数连续性和几何连续性。对连续性的概念有个认识后，在使用OPEN CASCADE或其他几何造型内核时，当出现需要指定连续性的时候，不至于茫然无措。

2.Parametric Continuity

利用函数曲线的可微性，曲线在连接处具有直到n阶连续导矢，即n次连续可微，这类光滑度称之为Cn或n阶参数连续性。下面给出参数连续性Parametric Continuity的定义：

参数曲线C(u)在u=u0处为k阶参数连续（Ck连续）的充要条件是：C(u)的每个分量在u=u0处Ck连续，即

OPEN CASCADE Curve Continuity

如果对所有的u∈[a,b]，曲线C(u)均Ck连续，则称它为关于参数u的Ck连续曲线。在函数曲线里，可微性和光滑度是一致的，函数曲线是C1连续，意味着具有连续的切矢；C2连续意味着不仅具有连续的切矢，还具有连续的曲率。由于曲线的参数选取并不唯一，同样的曲线可以有不同的参数表示，而曲线的参数连续又与参数选取紧密相关。若参数变换前曲线为Ck连续，但曲线的参数变换后可能不能在每一点处都满足Ck连续。这是个问题。

3.Geometric Continuity

实际工程设计中，人们有一种直观的感觉：两线段相连接，只要在连接点有相同的切线就认为是光滑的。但按照参数连续性度量光滑度，还必须有相同的切矢模长才能认为是C1连续的。由于参数连续性不能客观准确度量参数曲线连接的光滑度，因而经常用称之为几何连续性（Geometric Continuity）的方法来度量曲线的光滑程度。下面给出几何连续性的定义：

参数曲线C(u)是k阶几何连续的充要条件为：在弧长参数化下，曲线是Ck的。因为在弧长参数化下，曲线的参数连续与几何连续是一致的。

关于弧长参数化相关概念可参考： http://www.cppblog.com/eryar/archive/2014/08/25/208127.html

合成曲线在拼接点处满足不同于Cn连续性的某一组约束条件，称为具有n阶几何连续性，简记为Gn。事实上模型的形状是与描述它所取的参数无关的，作为形状的内在几何特征的光滑度及作为度量光滑度的几何连续性定义应该是独立于具体的参数化的。几何连续性放宽了对参数曲线光滑度的限制条件，为形状定义和形状控制提供了更多的自由度，更适合曲线在交互设计中使用，有文献称其为视觉连续性。

4.Curve Continuity

下面通过一个具体的例子来说明参数连续性和几何连续性。最后介绍OPEN CASCADE中对曲线连续性的定义。

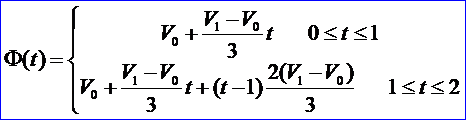
OPEN CASCADE Curve Continuity

Φ(t)在[0，2]上表示一条连接V0，V1的直线段，但却有

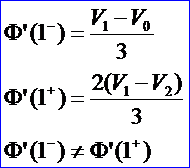
OPEN CASCADE Curve Continuity

Φ(t)明明是一条直线，却非C1连续，说明用参数连续性描述光滑性是不恰当的。

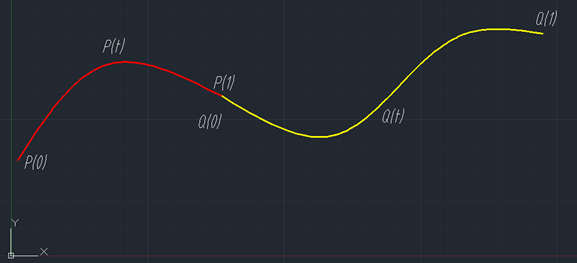
OPEN CASCADE Curve Continuity

Figure 4.1 两条曲线拼接的连续性

如4.1所示，对于参数t∈[0，1]的两条曲线P(t)和Q(t)，若要求在拼接处达到G0连续或C0连续，即两曲线在拼接处位置连续，则需要P(1) = Q(0)；

若要求在拼接处达到G1连续，就是说两条曲线在拼接处满足G0连续的条件下，并有公共的切矢：

当α＝1时，G1连续就成为C1连续。

若要求在拼接处达到G2连续，就是说两条曲线在拼接处满足G1连续的条件下，并有公共的曲率矢。根据曲率计算公式：

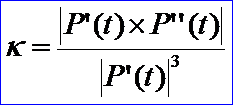
OPEN CASCADE Curve Continuity

则

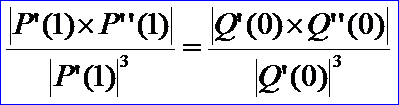
OPEN CASCADE Curve Continuity

将G1连续的条件方程代入可得：

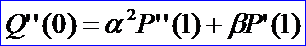
OPEN CASCADE Curve Continuity

β为任意常数。当α＝1，β＝0时，G2连续就成为了C2连续。至此可以看到，C1连续保证G1连续，C2连续保证G2连续，但反过来不行。也就是说Cn连续的条件比Gn连续的条件要苛刻。

OPEN CASCADE中关于曲线是连续性的定义使用了GeomAbs_Shape枚举定义：

//! Provides information about the continuity of a curve: //! -   C0: only geometric continuity. //! -   G1: for each point on the curve, the tangent vectors //! "on the right" and "on the left" are collinear with the same orientation. //! -   C1: continuity of the first derivative. The "C1" curve is //! also "G1" but, in addition, the tangent vectors " on the //! right" and "on the left" are equal. //! -   G2: for each point on the curve, the normalized //! normal vectors "on the right" and "on the left" are equal. //! -   C2: continuity of the second derivative. //! -   C3: continuity of the third derivative. //! -   CN: continuity of the N-th derivative, whatever is the //! value given for N (infinite order of continuity). //! Also provides information about the continuity of a surface: //! -   C0: only geometric continuity. //! -   C1: continuity of the first derivatives; any //! isoparametric (in U or V) of a surface "C1" is also "C1". //! -   G2: for BSpline curves only; "on the right" and "on the //! left" of a knot the computation of the "main curvature //! radii" and the "main directions" (when they exist) gives the same result. //! -   C2: continuity of the second derivative. //! -   C3: continuity of the third derivative. //! -   CN: continuity of any N-th derivative, whatever is the //! value given for N (infinite order of continuity). //! We may also say that a surface is "Ci" in u, and "Cj" in v //! to indicate the continuity of its derivatives up to the order //! i in the u parametric direction, and j in the v parametric direction. enum GeomAbs_Shape {   GeomAbs_C0,   GeomAbs_G1,   GeomAbs_C1,   GeomAbs_G2,   GeomAbs_C2,   GeomAbs_C3,   GeomAbs_CN };

结合前面关于参数连续和几何连续的介绍，再看头文件中的注释就很好理解了。

5.Conclusion

综上所述，对拼接曲线光滑度进行度量有两种方法：参数连续性和几何连续性。参数连续性是严格的数学可微性定义，就像别人对你到了年纪还没结婚的看法……“肯定是要求太高了”。而几何连续性就像我们工科专业的，不是那么喜欢较真，差不多就可以了。对有些精确结果还喜欢乘以一个经验系数，放点余量。理解了对拼接曲线光滑性的度量方法，就可以在用到的时候按需选择。