转载

DFS应用——遍历有向图+判断有向图是否有圈

【0】README

0.1）本文总结于数据结构与算法分析，源代码均为原创，旨在理解 “DFS应用——遍历有向图+判断有向图是否有圈” 的idea 并用源代码加以实现；

0.2）判断有向图是否有圈的rule——一个有向图是无圈图当且仅当它没有背向边，背向边定义，参见： http://blog.csdn.net/pacosonswjtu/article/details/49967255

【1】有向图相关

1.1）对有向图进行DFS的idea：利用与无向图相同的思路，也可以通过深度优先搜索以线性时间遍历有向图。如果图不是强连通的，那么从某个节点开始的DFS可能访问不了所有的节点。在这种情况下，我们在某个未作标记的节点处开始，反复执行DFS，直到所有节点都被访问到；

1.2）基于以上描述，我们看个荔枝（这只是一种可能的case）：

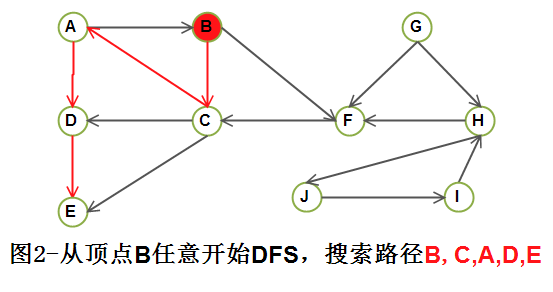
step1）从顶点B 任意开始深度优先搜索，访问顶点B, C, A, D, E；
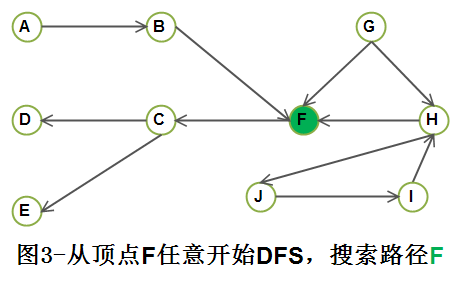
step2）从顶点 F 任意开始DFS，访问顶点 F；
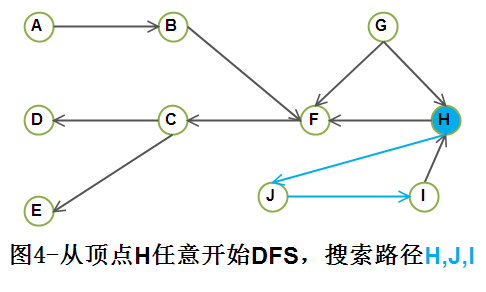
step3）从顶点 H 任意开始DFS，访问顶点 H, J, I；
step4）从顶点 G 任意开始DFS，访问顶点 G；

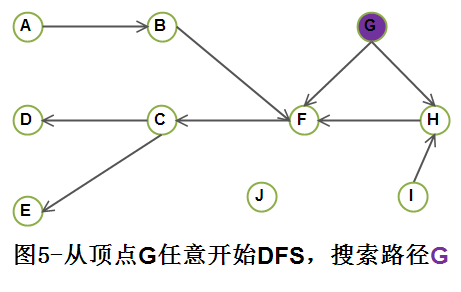
1.3）对于以上的DFS过程，对应的搜索优先搜索树如下图所示：

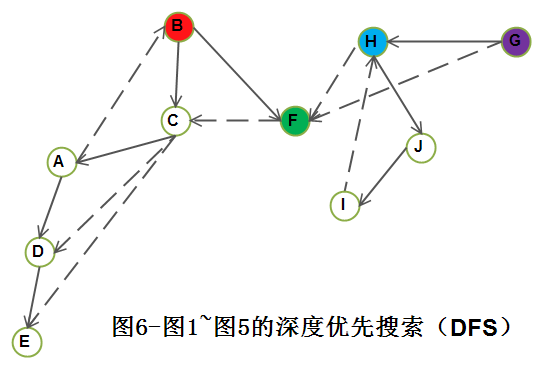对上图的分析（Analysis）：

A1）深度优先生成森林中虚线箭头是一些（v, w）边，其中的w 在考察时已经做了标记；
A2）我们看到，存在三种类型的边并不通向新顶点：
- A2.1）背向边：如（A，B）和（I，H）；
- A2.2）前向边：如（C，D）和（C，E），它们从树的一个节点通向一个后裔；
- A2.3）交叉边：如（F，C）和（G，F），它们把不直接相关的两个树节点连接起来；
A3）深度优先搜索森林一般通过吧一些子节点和一些新的树从左到右添加到森林中形成。在以这种方式构成的有向图的深度优先搜索中，交叉边总是从右到左进行的；

1.4）深度优先搜索（DFS）的一个用途是：检测一个有向图是否是无圈图；

4.1）法则如下：一个有向图是无圈图当且仅当它没有背向边；（上面的图有背向边，因此它不是无圈图）
4.2）拓扑排序也可以用来确定一个图是否是无圈图。 进行拓扑排序的另一种方法是通过深度优先生成森林的后序遍历给顶点指定拓扑编号N， N-1， ..., 1; 只要图是无圈的，这种排序就是一致的；

【2】source code + printing results（此处的dfs是对原始dfs修改而成的，与原始的dfs不同，但idea一样）

2.1）download source code： https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter9/p248_dfs_directed_graph

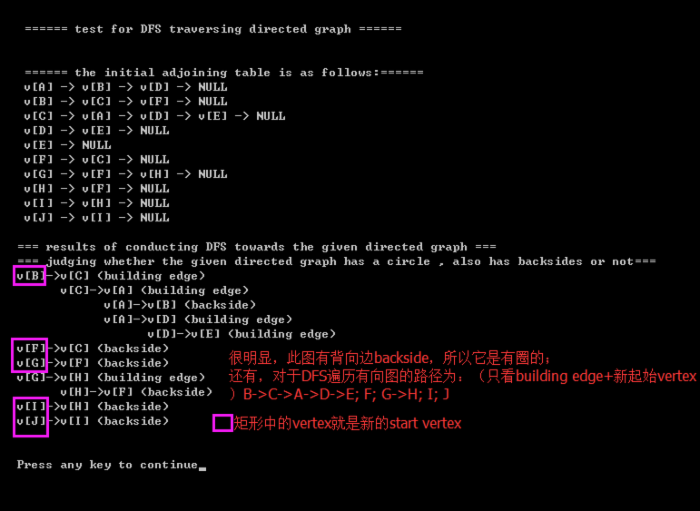
2.2）source code at a glance：（for complete code , please click the given link above）

void dfs(Vertex vertex, int depth) {  int i;  int visitFlag;  AdjTable temp;  Vertex adjVertex;     //printf("/n/t visited[%c] = 1 ", flag[vertex]);  visited[vertex] = 1; // update visited status of vertex  vertexIndex[vertex] = counter++; // number the vertex with counter  temp = adj[vertex];   visitFlag = 0;    while(temp->next)  {       adjVertex = temp->next->vertex;     if(visited[adjVertex]) // judge whether the adjVertes was visited before     {    if(vertexIndex[vertex] > vertexIndex[adjVertex] && parent[vertex] != adjVertex)      {     parent[adjVertex] = vertex; // building back side, attention of condition of building back side above          // just for printing effect     for(i = 0; i < depth; i++)        printf("      ");     printf("  v[%c]->v[%c] (backside) /n", flag[vertex], flag[adjVertex]);    }      }      //if(!visited[adjVertex])   else   {    if(vertex == start)     visitFlag = 1;    parent[adjVertex] = vertex;        // just for printing effect    for(i = 0; i < depth; i++)       printf("      ");       printf("  v[%c]->v[%c] (building edge) /n", flag[vertex], flag[adjVertex]);    dfs(adjVertex, depth+1);   }    if(vertex == start && visitFlag) //conducingt dfs for only one adjoining vertex in the given graph    break;    temp = temp->next;   }  }

2.3）printing results：
DFS应用——遍历有向图+判断有向图是否有圈