队列的实现:公式化描述
队列也是一种特殊的线性表。队列的插入和删除操作分别在线性表的两端进行,因此,队列是一个先进先出( first-in-first-out, FIFO)的线性表。
1、抽象数据类型
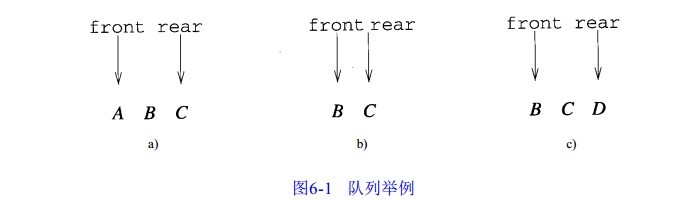
定义:队列( q u e n e)是一个线性表,其插入和删除操作分别在表的不同端进行。添加新元素的那一端被称为队尾 ( r e a r ),而删除元素的那一端被成为队首 ( f r o n t )。
所以,队列是一个先进先出( F I F O)的线性表,而堆栈是一个先进后出( L I F O)的线性表。
ADT:

2、公式化描述
队列可以用数组描述也可以用链表描述,此处先以数组即公式化的描述实现
第一种方式:location(i)=i-1
把数组q u e u e [ M a x S i z e ] 描述成一个队列,那么第一个元素为 q u e u e [ 0 ],第二个元素为 q u e u e [ 1 ],…。 f r o n t总是为 0, r e a r始终是最后一个元素的位置,队列的长度为 r e a r + 1 。对于一个空队列,有 r e a r =- 1 。

向队列中添加一个元素时,需要把 r e a r增1 ,并把新元素放入 q u e u e [ r e a r ]。这意味着一次添加操作所需要的时间为 O ( 1 )。删除一个元素时,把位置 1 至位置n的元素分别左移一个位置,因此删除一个元素所花费的时间为 O( n ),其中 n为删除完成之后队列中的元素数。如此看来,公式应用于堆栈,可使堆栈的插入和删除操作均耗时O ( 1 ),而应用于队列,则使队列的删除操作所需要的时间达到O ( n )。
第二种方式:
loacation(i)=location(1)+i-1
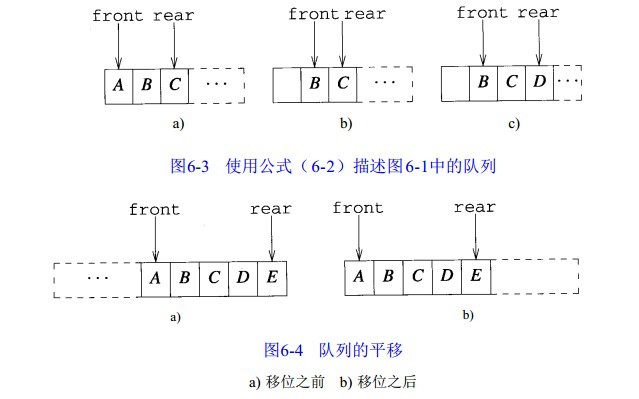
从队列中删除一个元素时,公式不要求把所有的元素都左移一个位置,只需简单地把 location ( 1 )增加 1 即可。每次删除操作将导致 f r o n t右移一个位置。当 r e a r < M a x S i z e - 1 时才可以直接在队列的尾部添加新元素。若 r e a r = M a x S i z e - 1 且f r o n t > 0时(表明队列未满) ,为了能够继续向队列尾部添加元素,必须将所有元素平移到队列的左端(如图 6 - 4所示),以便在队列的右端留出空间。对于使用公式( 1 )的队列来说,这种平移操作将使最坏情况下的时间复杂性增加O( 1 ),而对于使用公式(2)的队列来说,最坏情况下的时间复杂性则增加了O ( n )。所以,使用公式(2)在提高删除操作执行效率的同时,却降低了添加操作的执行效率。
第三种方式:
location(i)=(location(1)+i-1)%MaxSize
队列的添加和删除操作在最坏情况下的时间复杂性均变成 O( 1 )。这时,用来描述队列的数组被视为一个环(如图 所示) 。在这种情况下,对 f r o n t的约定发生了变化,它指向队列首元素的下一个位置(逆时针方向) ,而 r e a r的含义不变。向图 a中的队列添加一个元素将得到图 b 所示的队列,而从图 b 的队列中删除一个元素则得到图c 所示的队列。
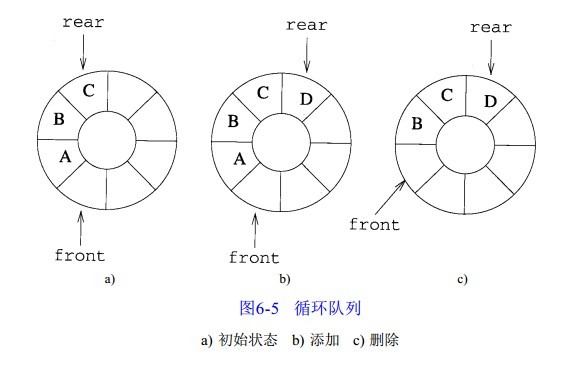
当且仅当 front=rear 时队列为空。初始条件f r o n t = r e a r = 0定义了一个初始为空的队列。现在需要确定队列为满的条件。如果不断地向图 6-5b 的队列添加元素,直到队列满为止,这时有 f r o n t = r e a r,竟然与队列为空的条件完全一样!因此,我们无法区分出队列是空还是满。为了避免这个问题,可以不允许队列被填满。为此,在向队列添加一个元素之前,先判断一下本次操作是否会导致队列被填满,如果是,则报错。因此,队列的最大容量实际上是 M a x S i z e - 1。
3、C++代码实现
队列定义:
1 #ifndef ARRAYQUEUE_H 2 #define ARRAYQUEUE_H 3 #include <iostream> 4 #include <new> 5 6 #include "exceptionerror.h" 7 template<class T> 8 class ArrayQueue 9 { 10 11 public: 12 ArrayQueue(const int &MaxQueueSize = 10); 13 ~ArrayQueue() 14 { 15 if (queue!=NULL) 16 { 17 delete[] queue; 18 } 19 } 20 bool IsEmpty()const{ return front == rear; } 21 bool IsFull()const{ return (((rear + 1) % MaxSize == front) ? true : false); } 22 T First()const; 23 T Last()const; 24 ArrayQueue<T>& Add(const T& x); 25 ArrayQueue<T>& Delete(T& x); 26 int Quality()const;//返回队列中的元素个数 27 friend std::ostream& operator<<(std::ostream & output, const ArrayQueue<T>& q) 28 { 29 if (q.IsEmpty()) 30 { 31 output << "queue is empty" << std::endl; 32 return output; 33 } 34 35 for (int i = (q.front + 1) % q.MaxSize; i <= q.rear; (++i) %= q.MaxSize) 36 { 37 output << q.queue[i] << " "; 38 } 39 40 output << std::endl; 41 return output; 42 } 43 private: 44 int front; 45 int rear; 46 int MaxSize; 47 T *queue; 48 }; 49 50 template<class T> 51 ArrayQueue<T>::ArrayQueue(const int &MaxQueueSize=10):MaxSize(MaxQueueSize+1),front(0),rear(0) 52 { 53 if (MaxSize>1) 54 { 55 try 56 { 57 queue = new T[MaxSize]; 58 } 59 catch (const std::bad_alloc& e) 60 { 61 std::cerr << "memory error" << std::endl; 62 } 63 64 } 65 } 66 67 template<class T> 68 T ArrayQueue<T>::First()const 69 { 70 if (IsEmpty()) 71 throw OutofBounds(); 72 73 return queue[(front + 1) % MaxSize]; 74 } 75 76 template<class T> 77 T ArrayQueue<T>::Last()const 78 { 79 if (IsEmpty()) 80 throw OutofBounds(); 81 82 return queue[rear%MaxSize]; 83 } 84 85 template<class T> 86 ArrayQueue<T>& ArrayQueue<T>::Add(const T& x) 87 { 88 if (IsFull()) 89 throw NoMem(); 90 rear = (rear + 1) % MaxSize; 91 queue[rear] = x; 92 return *this; 93 } 94 95 template<class T> 96 ArrayQueue<T>& ArrayQueue<T>::Delete(T& x) 97 { 98 if (IsEmpty()) 99 { 100 throw OutofBounds(); 101 } 102 103 front = (front + 1) % MaxSize; 104 x = queue[front]; 105 return *this; 106 } 107 108 template<class T> 109 int ArrayQueue<T>::Quality()const 110 { 111 if (IsEmpty()) 112 { 113 return 0; 114 } 115 else if (IsFull()) 116 { 117 return MaxSize-1; 118 } 119 120 if ((front+1)%MaxSize<rear) 121 { 122 return rear - (front+1)%MaxSize+1; 123 } 124 else 125 { 126 return MaxSize-(front - rear); 127 } 128 129 } 130 131 #endif
exceptionerror.h定义:

1 #ifndef OUTOFBOUND_H 2 #define OUTOFBOUND_H 3 #include <iostream> 4 class OutofBounds 5 { 6 public: 7 OutofBounds() 8 { 9 std::cerr << "Out of Bounds" << std::endl; 10 //std::exit(1); 11 } 12 }; 13 14 class NoMem 15 { 16 public: 17 NoMem(){ 18 std::cerr << "No Memory" << std::endl; 19 //std::exit(1); 20 } 21 22 }; 23 #endifView Code
测试:
1 #include "ArrayQueue.h" 2 3 int main() 4 { 5 ArrayQueue<int> Q; 6 Q.Add(1); 7 Q.Add(2); 8 Q.Add(1); 9 Q.Add(2); 10 Q.Add(1); 11 Q.Add(2); 12 Q.Add(1); 13 Q.Add(2); 14 std::cout << Q; 15 std::cout << Q.Quality() << std::endl; 16 int x; 17 Q.Delete(x); 18 std::cout << Q; 19 std::cout << Q.Quality() << std::endl; 20 system("pause"); 21 return 0; 22 }
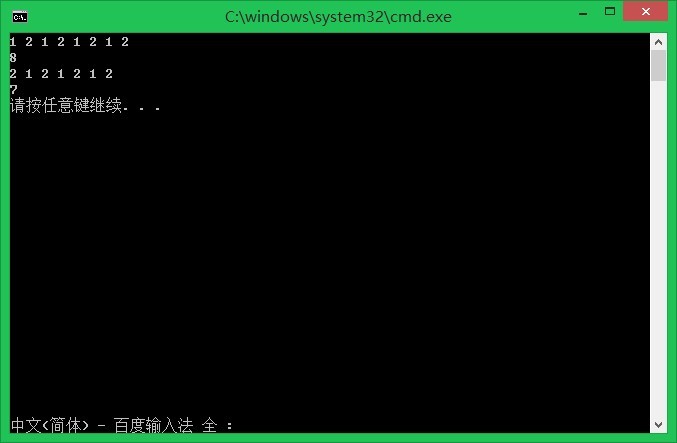
输出:











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

