遗传算法（二）之组卷算法
组卷算法主要用于编制科学、公正的试卷的一种算法，具体大家可以百度看一下。我这篇文章主要是讲解如何通过遗传算法来实现组卷，遗传算法大家不清楚的地方仍然可以查看百度，不是这篇文章的重点。
一、遗传算法的表示
基本遗传算法（SGA）可以定义为一个8 元数组：
。
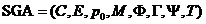其中：
C ：个体的编码， SGA 种一般采用固定长度的二进制编码；
E ：适应度评价函数；
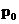：初始种群；
M ：群体大小，一般取 20 ；
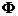：选择算子；
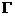：交叉算子；
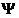：变异算子
T ：结束条件
二、遗传算法的设计
遗传算法的设计通常有以下5 个步骤：
1、编码方案的确定
编码对遗传算法的效率、解空间的收敛程度有很大的影响。如何把现实问题，转化为算法的使用的编码，也是一个难度比较大的问题。
2、选择适应度评价函数
好的适应度函数能把种群的优劣程度充分、准确的体现出来，能让遗传算法在目标空间中更快的找到近优解。
3、初始化参数
参数主要是包括：种群数目 M ，交叉概率，变异概率以及迭代的代数。
4、算子的设计
算子主要包括选择算子、交叉算子、变异算子等
5、终止条件
终止条件是要是根据求解的性质，在质量和效率上做出合理的均衡和侧重。
三、基于遗传算法的组卷实现
1、组卷问题的数学模型
一套题目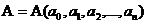 
包含 n 个属性指标，如：章节、难度、题型等；一套试题 
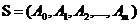是有 m 个题目数，这样就构成了一个 的矩阵。
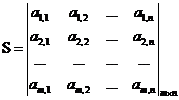
对于这个矩阵应该满足
（1）试卷的总分是一个常数 G ，例如 100 分；
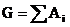
（ 2 ）各题型的分数也是一个常数，例如填空题多少分，选择题多少分。
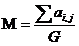是个常数， M 表示每个题型占总分的比例。
（ 3 ）各难度系数所占试卷的比值一般也是一个常数，
2、染色体的编码
题库中有 L 个待选题目，我们用一个长度为 L 的 01 字符串来表示， 0 表示题未被选中， 1 表示题选中。这样每一个试卷都对应了一个长度为 L 的二进制字符串，称为染色体。
3、目标函数
我们可以把上述约束条件转化为目标函数，设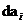 
（ i=1,....p,p 为要求的难度系统的总和）为难度要求为 i 的实际总分值与要求的总分值的偏差，偏差的平均值就为 
；
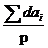同理，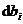 
（ i=1,...q,q 为试题的总类型数）为实际试题类型第 i 章所占的分数与试题要求的分数之间的偏差，偏差的平均值就为 
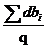；每种偏差要求的权重为 
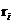其中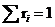 
那我们的目标函数就为:
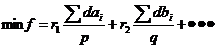
f越小选出的试题越好。
4、初始种群
一套试卷结构表为：
| 题型 | 填空题 | 选择题 | 判断题 | 简答题 | 综合题 |
| 总分数 | 10 | 10 | 10 | 30 | 40 |
| 每题分数 | 1 | 1 | 1 | 10 | 20 |
| 数目 | 10 | 10 | 10 | 3 | 2 |
题库数据表
| 题型 | 填空题 | 选择题 | 判断题 | 简答题 | 综合题 |
| 每题分数 | 1 | 1 | 10 | 30 | 20 |
| 难度系数 | 0.85 ～ 1 | 0.76 ～ 0.86 | 0.40 ～ 0.76 | 0.23 ～ 0.39 | 0.0 ～ 0.22 |
| 数目 | 50 | 150 | 70 | 30 | 20 |
假设，一套试题总分 100 分，综合难度系统为 0.55 ，也就是说，期望得分为 55 分。
四、代码实现
参考背包问题的实现。
正文到此结束
热门推荐
相关文章
Loading...
![[HBLOG]公众号](http://www.liuhaihua.cn/img/qrcode_gzh.jpg)
