核密度估计（KDE） 相关知识
这周忙着写论文，技术实践这边就怠慢了，都是些修修补补的工作。比较有意思的就是接触到数据分析中的核密度估计方法。现将相关知识总结如下。
密度估计经常在统计学中作为一种基于有限的样本来估计其概率密度函数的方法。
下图是《数据之魅》中的一维数据的直方图和核密度估计的对比图，虚线框为直方图，两个实曲线描述的就是通过KDE估计的结果。
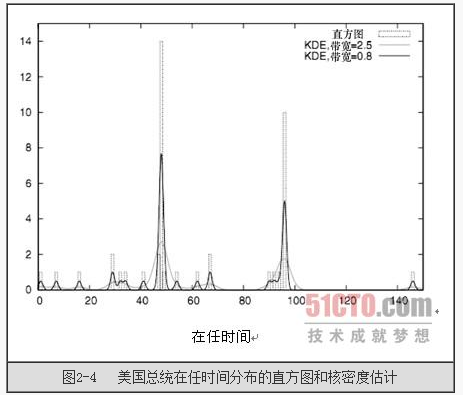
直方图不能很优雅地处理一些异常点。某个远离大部分点的异常点会造成图形中间的空白，或者迫使我们使用对大多数点来说过宽的矩形组。这些异常点可能会使我们很难依赖自动方式来确定一个合适的矩形宽度。幸运的是，还有另一种经典的直方图可供选择，它不存在上述的各种问题。它就是核密度估计(Kernel Density Estimate，KDE)。
核密度的方法就是借助一个移动的单元格（核函数）放在每一个数据点的位置上。然后将核函数的作用效果叠加起来，获得一条光滑的曲线。而核函数的选择条件为单个峰值下的函数面积为1
数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。
数据的归一化处理，即将数据统一映射到[0,1]区间上。
常用的核函数有：
- Box核函数： /( K(x) = /begin{aligned} /begin{cases} /frac{1}{2} & if |x| /leq 1 // 0 & other /end{cases} /end{aligned} /)
- Epanechnikov核函数：
- Gaussian核函数： 所以公式中的K(x-xi)为在点xi出的峰值 h为带宽，控制函数的蔓延
如果你正使用KDE 来生成图以使点分布直观可视，最好手动尝试并肉眼观察误差。最后，值得一提的是，并没有所谓的"正确"答案，只有最适合某个目的的答案。为了获得直观的理解，最佳方案也许并不是最小化一个特定的数学方面的量。
多元核密度估计 核密度估计方法在二十世纪的五六十年代第一次应用于单变量时被学界所知，针对多元数据的估计在90年代后才成熟。下图就是一个简单的应用核密度估计的过程，首先如左图，通过公式计算以每个点为中心的核，这些核的求和结果展示为右图的密度估计结果。 这样将Dx 扩展到多元变量上为
带宽的其他选择方法。 the plug-in method and the method of cross-validation
https://www.wikiwand.com/en/Multivariate kernel density_estimation wiki
正文到此结束
热门推荐
相关文章
近期评论
-
你这基本没有更新呀，最近文章显示还是2019年的文章。不符合要求哈
-
关键词：慕云博客 链接：https://www.lilun.me 描述：分享原创文字的个人博客
-
-
-
可以提供一下源码吗
-
不是商业站，鸡娃学习笔记
-
-
-
-
听他们说很厉害的样子
Loading...
![[HBLOG]公众号](http://www.liuhaihua.cn/img/qrcode_gzh.jpg)
