烧脑的方块：解析“俄罗斯方块”４种不同的基础模块
本文授权转自知乎作者 @ Thinkraft 对 4D俄罗斯方块有多少种不同的基础模块？ 的回答，未经作者本人同意不可转载。
俄罗斯方块这种休闲游戏大家基本玩过，尤其是童年时期在电视机和掌机上都有不少这类型的游戏。其基本规则是移动、旋转和摆放游戏自动输出的各种方块，使之排列成完整的一行或多行并且消除得分。这边脑洞一下，我们接触的大部分是2维的，若是3维、4维的呢？俄罗斯方块会能有多少种不同的基础模块？
二维
平面上一个坐标（基准位置）为x、y，边长为a的正方形，我这么表示它的四个顶点坐标：([x, x+a], [y, y+a])
在一个轴上不变，另一个轴上平移±a，可以得到一个和它相接的正方形，这两个正方形之间有一条边是重合的。
构造所谓「基础型」（Tetrimino）时，有两个原则：
-
沿x或y轴任意一轴，以a为单位进行任意距离平移，即 x2 = x1 + na; y2 = y1 + na，得到的图形和原图形等价。
-
绕虚设的z轴进行90度旋转，即x2 = y1; y2 = -x1，得到的图形和原图形等价。
为了简化描述，这里再转换一下坐标系：设正方形边长是1，第一个正方形的坐标是(0,0)。
显然，两个正方形的情况下，不管怎么连接都等价于这个：(0, 0), (1, 0)
三个正方形的情况下，可以连接成两种形状：
(0, 0), (1, 0), (0, 1)
(0, 0), (1, 0), (2, 0)
增加到第四个正方形的时候，需要在之前的形状上选择一个邻接面。也就是「选择一个正方形」，「再选一个轴」，「再选一个方向」。
得到的排列组合中，去掉不合法的（有时第四个正方形会和之前的正方形重叠），再去掉等价重复的，最后就是你知道的7种形状：
(0, 0), (1, 0), (0, 1), (-1, 0) -- T
(0, 0), (1, 0), (0, 1), (1, 1) -- O
(0, 0), (1, 0), (0, 1), (1, -1) -- S
(0, 0), (1, 0), (0, 1), (2, 0) -- J
(0, 0), (1, 0), (0, 1), (0, 2) -- L
(0, 0), (1, 0), (0, 1), (-1, 1) -- Z
(0, 0), (1, 0), (2, 0), (3, 0) -- I
注意，除了直棍I以外的所有形状，都可以看成是L型的衍伸，也就是说只重点考虑L型即可。
三维的情况类似
首先，多了一个实际存在的z轴。空间中正方体的八个顶点的坐标为：([x, x+a], [y, y+a], [z, z+a])
保持其中两个轴不变，另一个轴上平移±a可以得到一个和原正方体相接的正方体。它们之间有一个面重合。
构造三维版的基础型（Tetracube）时中，被视为等价的变换除了平移外，绕其中任意一轴以90度为单位旋转也包括在内。
于是，三个正方体的情况下，可以连接成两种形状：
(0, 0, 0), (1, 0, 0), (0, 1, 0)
(0, 0, 0), (1, 0, 0), (2, 0, 0)
再加一个正方体，利用上面的原则，可以得到这些不重复的形状：
(0, 0, 0), (1, 0, 0), (0, 1, 0), (-1, 0, 0) -- T
(0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1) -- （没名字，我这里暂称W）
(0, 0, 0), (1, 0, 0), (0, 1, 0), (1, 1, 0) -- O
(0, 0, 0), (1, 0, 0), (0, 1, 0), (1, -1, 0) -- S
(0, 0, 0), (1, 0, 0), (0, 1, 0), (1, 0, 1) -- （暂称V）
(0, 0, 0), (1, 0, 0), (0, 1, 0), (1, 0, -1) -- （暂称逆V）
(0, 0, 0), (1, 0, 0), (0, 1, 0), (2, 0, 0) -- L
(0, 0, 0), (1, 0, 0), (2, 0, 0), (3, 0, 0) -- I
注意，三维空间下，不再区分S与Z、J与L。二维平面中的对称形状只能通过翻转得到，光靠旋转是不能实现的；而三维空间中由于x和y轴也都变成了可旋转的了，等于获得了翻转二维形状的能力。新引入的「V」和「逆V」具有手性，无法通过三维旋转互换。
四维
到了四维，又多了一个轴，因此「超正方体」拥有16个顶点，坐标变成了这样：([x, x+a], [y, y+a], [z, z+a], [m, m+a])
构造相接超正方体的原则相同，保持三个轴不变，只在一个轴上平移a。得到的超正方体和之前的超正方体之间有一个「正方体」是重合的。
不同点是关于旋转，这里认为在四维空间下，某个点能够绕着一个平面旋转，例如点(x, y, z, m)绕着平面xy正向旋转90度，则坐标会变为(x, y, m, -z)。
和之前一样，我们允许任意平移、旋转。在只有三个超正方体的时候，它们的连接依然只有两种形状。
(0, 0, 0, 0), (1, 0, 0, 0), (0, 1, 0, 0)
(0, 0, 0, 0), (1, 0, 0, 0), (2, 0, 0, 0)
在这两种形状的基础上再增加一个超正方体，得到的独特组合如下：
(0, 0, 0, 0), (1, 0, 0, 0), (0, 1, 0, 0), (-1, 0, 0, 0) -- T
(0, 0, 0, 0), (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0) -- W
(0, 0, 0, 0), (1, 0, 0, 0), (0, 1, 0, 0), (1, 1, 0, 0) -- O
(0, 0, 0, 0), (1, 0, 0, 0), (0, 1, 0, 0), (1, -1, 0, 0) -- S
(0, 0, 0, 0), (1, 0, 0, 0), (0, 1, 0, 0), (1, 0, 1, 0) -- V
(0, 0, 0, 0), (1, 0, 0, 0), (0, 1, 0, 0), (2, 0, 0, 0) -- L
(0, 0, 0, 0), (1, 0, 0, 0), (2, 0, 0, 0), (3, 0, 0, 0) -- I
注意，由于多引入了一个轴，原三维空间下的「V」和「逆V」也变成等价互换的了。所以，四维空间下，由四个超正方体构成的基础型共有7种形状。
光是这么说可能难以理解，来张图感受一下吧：
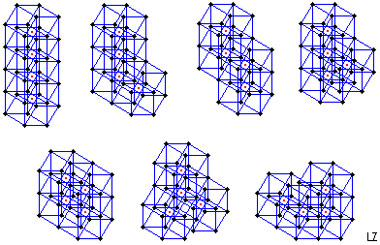
PS. 本文由作者 @ Thinkraft 授权转载自CocoaChina网站，其他网站未经作者允许不得转载。另请勿转载至微信、微博公众号。
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
