集合的异或运算（对称差）
1、集合的异或运算(AΔB)定义
属于A或属于B，但不同时属于A和B的元素的集合称为A和B的对称差，即A和B的异或。 
注：草绿色部分即为 AΔB
2、对称差(异或)运算的定律
2.1 AΔB = (A-B)∪(B-A) = (A∪B)-(A∩B)
该公式的证明已在集合的证明及相关习题 中证明了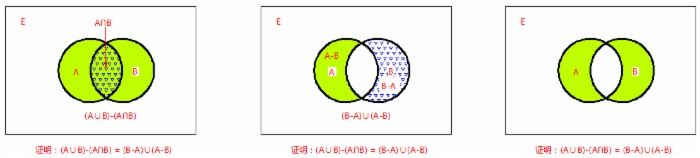
2.2 对称差运算的交换律
(AΔB)ΔC = (AΔC)ΔB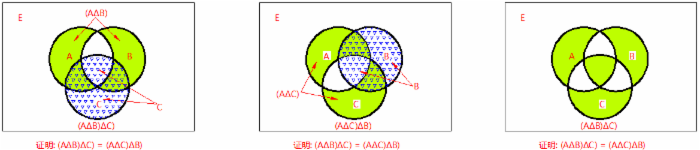 
注：图1中草绿色部分为 (AΔB) ，三角形区域为 C ，(AΔB)ΔC = 仅含草绿色或仅含三角形的区域注：图2中草绿色部分为 (AΔC) ，三角形区域为 B ，(AΔC)ΔB = 仅含草绿色或仅含三角形的区域
证明：
(AΔB)ΔC= [(A-B)∪(B-A)]△C
= {[(A-B)∪(B-A)] - C} ∪ {C - [(A-B)∪(B-A)]}
转换全部 '-' 号
= {[(A∩～B)∪(～A∩B)] ∩ (～C)} ∪ {C∩～[(A∩～B)∪(～A∩B)]}
对大括号的2部分分别进行公式化解
左边部分：
{[(A∩～B)∪(～A∩B)] ∩ (～C)}
将(A∩～B)和(～A∩B)当整体，根据分配律
{[(A∩～B)∪(～A∩B)] ∩ (～C)}
= {[(A∩～B)∩(～C)]∪[(～A∩B)∩(～C)]}
根据结合律
= {(A∩～B∩～C)∪(～A∩B∩～C)}
右边部分：
{C∩～[(A∩～B)∪(～A∩B)]}
根据De.Morgen定律，将～移进去
= {C∩[～(A∩～B)∩～(～A∩B)]}
根据De.Morgen定律，继续将～移进去
= {C∩[(～A∪～～B)∩(～～A∪～B)]}
∵～～B = B，～～A = A
∴{C∩[(～A∪～～B)∩(～～A∪～B)]} = {C∩[(～A∪B)∩(A∪～B)]}
将(～A∪B)当作整体，继续用分配律处理[(～A∪B)∩(A∪～B)]
[(～A∪B)∩(A∪～B)]
= [(～A∪B)∩A]∪[(～A∪B)∩～B)]
继续分配律
= [(～A∩A)∪(B∩A)]∪[(～A∩～B)∪(B∩～B)]
= [φ∪(B∩A)]∪[(～A∩～B)∪φ]
= (B∩A)∪(～A∩～B)
∴{C∩[(～A∪B)∩(A∪～B)]} = {C∩(B∩A)∪(～A∩～B))
将(B∩A)和(～A∩～B)分别当作整体，根据分配律
= (A∩B∩C)∪(～A∩～B∩C)
∴(AΔB)ΔC = {(A∩～B∩～C)∪(～A∩B∩～C)} ∪ (A∩B∩C)∪(～A∩～B∩C)
根据以上步骤，将B看着C，同理可推得：
(AΔC)ΔB = {(A∩～C∩～B)∪(～A∩C∩～B)} ∪ (A∩C∩B)∪(～A∩～C∩B)
根据结合律：
(AΔC)ΔB = {(A∩～B∩～C)∪(～A∩B∩～C)} ∪ (A∩B∩C)∪(～A∩～B∩C)
∴(AΔB)ΔC = (AΔC)ΔB
点评：该证明过程重点在于将2个类似的式子转化为可用结合律移动位置的中间表达式，从而得证
3、集合的异或运算在计算机中的应用
证明：当 AΔB = C 时，AΔC = B
即典型的异或运算 A xor B = C，A xor C = B
在编程中常用该可逆运算对数据 B 异或一个常量 A 转换后进行加密保护，当要还原数据B时，再次用 C 异或常量 A 即可得到B
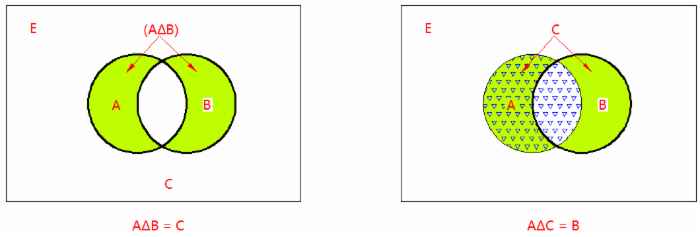
注:图1中草绿色部分即为 AΔB = C
图2中草绿色部分即为 C，三角形区域为 A，AΔC = 仅有草绿色或仅有三角形的区域 = B
证明：
∵AΔB = C∴C = (A∪B)-(A∩B)
将C代入到AΔC中
AΔC = AΔ[(A∪B)-(A∩B)]
= {A∪[(A∪B)-(A∩B)]} - {A∩[(A∪B)-(A∩B)]}
先处理左边式子
{A∪[(A∪B)-(A∩B)]}
= A∪{(A∪B)∩[～(A∩B)]}
将 (A∪B) 和 [～(A∩B)]看着整体，根据分配律
= [A∪(A∪B)] ∩ {A∪[～(A∩B)]}
= (A∪B) ∩ {A∪[～(A∩B)]}
根据De.morgen定律
= (A∪B) ∩ {A∪[～A∪～B)]}
= (A∪B) ∩ {(A∪～A)∪～B}
= (A∪B) ∩ {E∪～B}
= (A∪B) ∩ E
= (A∪B)
再处理右边式子
{A∩[(A∪B)-(A∩B)]}
= A∩{(A∪B)∩[～(A∩B)]}
= A∩(A∪B)∩[～(A∩B)]
根据吸收律反推
A∩(A∪B) = A
A∩(A∪B)∩[～(A∩B)] = A∩[～(A∩B)]
合并左右式子
AΔC = (A∪B) - {A∩[～(A∩B)]}
将[～(A∩B)]看着整体，根据De.morgen定律
(A∪B) - {A∩[～(A∩B)]} = (A∪B) ∩ {～ {A∩[～(A∩B)]}}
再次根据De.morgen定律
= (A∪B) ∩ {～A∪～[～(A∩B)]}
= (A∪B) ∩ {～A∪(A∩B)}
= (A∪B) ∩ {～A∪(A∩B)}
根据分配律
= (A∪B) ∩ {(～A∪A)∩(～A∪B)}
= (A∪B) ∩ {E∩(～A∪B)}
= (A∪B) ∩ (～A∪B)
根据分配律倒推
= B∪(A∩～A)
= B∪(φ)
= B
∴AΔC = B
《离散数学及其应用》第6版P83 21 题
证明：当 AΔB = AΔC时，是否有B = C
即如果2个数和同一个常量 A 进行异或后的结果相等，那么这两个数必定相等，这是 ∪∩ 等运算没有的性质证明：
∵AΔB = AΔC = D根据上面证明：当 AΔB = D 时，AΔD = B(将上面证明中的C换成D，以免歧义)
同理
∵AΔC = D
∴AΔD = C = B
∴C = B
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
