SLAM拾萃(1)：octomap

前言

大家好，时隔多年之后，我又开始了博客旅程。经历了很多事情之后呢，我发现自己的想法真的很简单：好好读书做课题，闲下来时写写博客，服务大家。所以我会继续写SLAM相关的博客。如果你觉得它对你有帮助，那是最好不过的啦！写作过程中得到了许多热心读者的帮助与鼓励，有些读者还成了要好的朋友，在此向大家致谢啦！关于SLAM，读者也会有很多问题。由于我个人精力和学力都有限，无法一一回答，向大家说声抱歉！有些共同的问题，我肯定会在博客里介绍的！

前两天刚从珠海开会回来，与中山大学的同学们聚在一起玩耍，很开心！

《一起做》系列已经结束，事实上它是我以前探索过程中的一些总结。虽然仍然有很多令人不满意的地方，不过相信读了那个系列，读者应该对SLAM的流程有一定的了解了。尤其是通过代码，你能知道许多论文里没讲清楚的细节。在这之后，我现在有两个规划。一是对目前流行的SLAM程序做一个介绍，沿着《视觉SLAM实战》往下写；二是介绍一些好用的开源工具/库，写成一个《SLAM拾萃》。我觉得这两部分内容，对读者了解SLAM会有较大的帮助。当然，如果你对我的博客有任何建议，可以在下方评论或给我发邮件。

本篇是《SLAM拾萃》第一篇，介绍一个建图工具：octomap。和往常一样，我会介绍它的原理、安装与使用方式，并提供例程供读者学习。必要时也会请小萝卜过来吐槽。（小萝卜真是太好用了，它可以代替读者提很多问题。）

什么是octomap？

RGBD SLAM的目的有两个：估计机器人的轨迹，并建立正确的地图。地图有很多种表达方式，比如特征点地图、网格地图、拓扑地图等等。在《一起做》系列中，我们使用的地图形式主要是点云地图。在程序中，我们根据优化后的位姿，拼接点云，最后构成地图。这种做法很简单，但有一些明显的缺陷：

• 地图形式不紧凑。
  点云地图通常规模很大，所以一个pcd文件也会很大。一张640$/times$480的图像，会产生30万个空间点，需要大量的存储空间。即使经过一些滤波之后，pcd文件也是很大的。而且讨厌之处在于，它的“大”并不是必需的。 点云地图提供了很多不必要的细节 。对于地毯上的褶皱、阴暗处的影子，我们并不特别关心这些东西。把它们放在地图里是浪费空间。
• 处理重叠的方式不够好。
  在构建点云时，我们直接按照估计位姿拼在了一起。 在位姿存在误差时，会导致地图出现明显的重叠 。例如一个电脑屏变成了两个，原本方的边界变成了多边形。对重叠地区的处理方式应该更好一些。
• 难以用于导航
  说起地图的用处，第一就是导航啦！有了地图，就可以指挥机器人从A点到B点运动，岂不是很方便的事？但是，给你一张点云地图，是否有些傻眼了呢？我至少得知道哪些地方可通过，哪些地方不可通过，才能完成导航呀！ 光有点是不够的 ！

octomap就是为此而设计的！亲，你没有看错，它可以优雅地压缩、更新地图，并且分辨率可调！它以八叉树（octotree，后面会讲）的形式存储地图，相比点云，能够省下大把的空间。octomap建立的地图大概是这样子的：（从左到右是不同的分辨率）

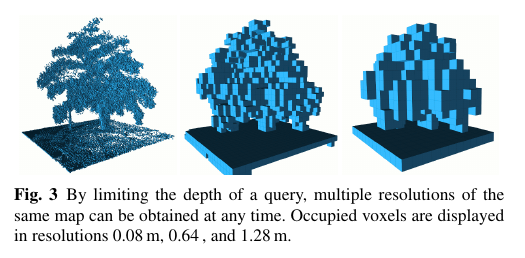
由于八叉树的原因，它的地图像是很多个小方块组成的（很像minecraft）。当分辨率较高时，方块很小；分辨率较低时，方块很大。每个方块表示该格被占据的概率。因此你可以查询某个方块或点“是否可以通过”，从而实现不同层次的导航。简而言之，环境较大时采用较低分辨率，而较精细的导航可采用较高分辨率。

小萝卜：师兄你这是介绍吗？真像广告啊……

octomap原理

本段会讲一些数学知识。如果你想“跑跑程序看效果”，可以跳过本段。

1. 八叉树的表达

八叉树，也就是传说中有八个子节点的树！是不是很厉害呢？至于为什么要分成八个子节点，想象一下一个正方形的方块的三个面各切一刀，不就变成八块了嘛！如果你想象不出来，请看下图：

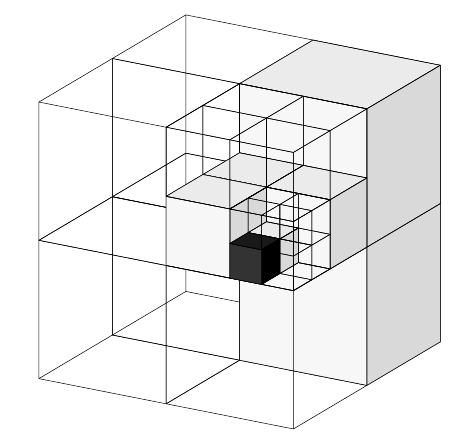
实际的数据结构呢，就是一个树根不断地往下扩，每次分成八个枝，直到叶子为止。叶子节点代表了分辨率最高的情况。例如分辨率设成0.01m，那么每个叶子就是一个1cm见方的小方块了呢！

每个小方块都有一个数描述它是否被占据。在最简单的情况下，可以用0－1两个数表示（太简单了所以没什么用）。通常还是用0～1之间的浮点数表示它被占据的概率。0.5表示未确定，越大则表示被占据的可能性越高，反之亦然。由于它是八叉树，那么一个节点的八个孩子都有一定的概率被占据或不被占据啦！（下图是一棵八叉树）

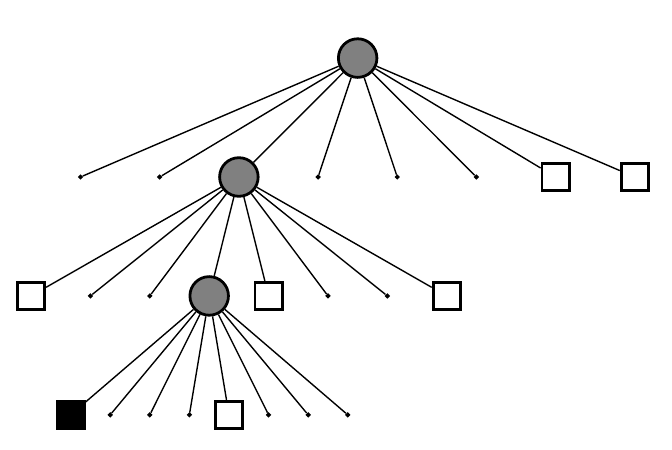
用树结构的好处时： 当某个节点的子结点都“占据”或“不占据”或“未确定”时，就可以把它给剪掉 ！换句话说，如果没必要进一步描述更精细的结构（孩子节点）时，我们只要一个粗方块（父节点）的信息就够了。这可以省去很多的存储空间。因为我们不用存一个“全八叉树”呀！

2. 八叉树的更新

在八叉树中，我们用概率来表达一个叶子是否被占据。为什么不直接用0－1表达呢？因为在对环境的观测过程中，由于噪声的存在，某个方块有时可能被观测到是“占据”的，过了一会儿，在另一些方块中又是“不占据”的。有时“占据”的时候多，有时“不占据”的时候多。这一方面可能是由于环境本身有动态特征（例如桌子被挪走了），另一方面（多数时候）可能是由于噪声。根据八叉树的推导，假设$t＝1，/ldots, T$时刻，观测的数据为$z_1, /ldots, z_T$，那么第$n$个叶子节点记录的信息为：$$ P(n|z_{1:T}) =  /left[ 1+ /frac{1-P(n|z_T)}{P(n|z_T)} /frac{1-P(n|z_{1:T-1})}{P(n|z_{1:T-1})} /frac{P(n)}{1-P(n)} /right]^{-1}  /quad /quad (1)$$

小萝卜：哇！又一个好长的式子！这说的是啥师兄？

师兄：哎，写论文非得把一些简单的事情写得很复杂。为了解释这东西，先讲一下 logit 变换。该变换把一个概率$p$变换到全实数空间$R$上： $$ /alpha = logit(p) = log /left( /frac{p}{1-p} /right) $$

这是一个可逆变换，反之有： $$ p = logit^{-1} (/alpha) = /frac{1} { 1+ exp(-/alpha) }. $$

$/alpha$叫做log-odds。我们把用$L()$叶子节点的log-odds，那么(1)就可以写成： $$ L( n| z_{1:T} ) = L(n|z_{1:T-1}) + L(n|z_T) $$

小萝卜：哦！这个我就懂了！每新来一个就直接加到原来的上面，是吧？

师兄：对，此外还要加一个最大最小值的限制。最后转换回原来的概率即可。

八叉树中的父亲节点占据概率，可以根据孩子节点的数值进行计算。比较简单的是取平均值或最大值。如果把八叉树按照占据概率进行渲染，不确定的方块渲染成透明的，确定占据的渲染成不透明的，就能看到我们平时见到的那种东西啦！

octomap本身的数学原理还是简单的。不过它的可视化做的比较好。下面我们来讲讲如何下载、安装八叉树程序，并给出几个小的例程。

安装octomap

octomap的网页见：https://octomap.github.io

它的github源码在：https://github.com/OctoMap/octomap

它还有ROS下的安装方式：http://wiki.ros.org/octomap

在开发过程中，可能需要不断地查看它的API文档。你可以自己用doxygen生成一个，或者查看在线文档：http://octomap.github.io/octomap/doc/

为了保持简洁，我们不要求读者安装ROS，仅介绍单独的octomap。我的编译环境是ubuntu 14.04。ubuntu系列的应该都不会有太大问题。

1. 编译octomap新建一个目录，拷贝octomap代码。如果没有git请安装git：sudo apt-get install git

1.  git clone https://github.com/OctoMap/octomap 

   git会把代码拷贝到当前目录/octomap下。进入该目录，参照README.md进行安装。编译方式和普通的cmake程序一样，如果你学过《一起做》就应该很熟悉了：

    1 mkdir build 2 cd build 3 cmake .. 4 make 

   事实上，octomap的代码主要含两个模块：本身的octomap和可视化工具octovis。octovis依赖于qt4和qglviewer，所以如果你没有装这两个依赖，请安装它们：sudo apt-get install libqt4-dev qt4-qmake libqglviewer-dev

   如果编译没有给出任何警告，恭喜你编译成功！

2. 使用octovis查看示例地图
   在bin/文件夹中，存放着编译出来可执行文件。为了直观起见，我们直接看一个示例地图：
   

    bin/octovis octomap/share/data/geb079.bt 

   octovis会打开这个地图并显示。它的UI是长这样的。你可以玩玩菜单里各种东西（虽然也不多，我就不一一介绍UI怎么玩了），能看出这是一层楼的扫描图。octovis是一个比较实用的工具，你生成的各种octomap地图都可以用它来看。（所以你可以把octovis放到/usr/local/bin/下，省得以后还要找。）

   

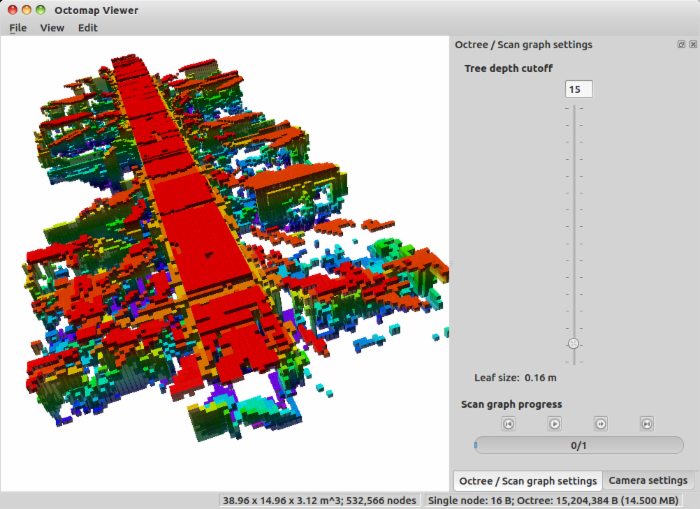
例程1：转换pcd到octomap

GUI玩够了吧？仅仅会用UI是不够滴，现在让我们开始编代码使用octomap这个库吧！

我为你准备了三个小例程。在前两个中，我会教你如何将一个pcd格式的点云地图转换为octomap地图。后一个中，我会讲讲如何根据g2o优化的轨迹，以类似slam的方式，把几个RGBD图像拼接出一个octomap。这对你研究SLAM会有一些帮助。所有的代码与数据都可以在我的github上找到。有关编译的信息，我写在这个代码的Readme中了，请在编译前看一眼如何编译这些代码。

源代码如下：src/pcd2octomap.cpp 这份代码将命令行参数1作为输入文件，参数2作为输出文件，把输入的pcd格式点云转换成octomap格式的点云。通过这个例子，你可以学会如何创建一个简单的OcTree对象并往里面添加新的点。

  1 #include <iostream>  2 #include <assert.h>  3   4 //pcl  5 #include <pcl/io/pcd_io.h>  6 #include <pcl/point_types.h>  7   8 //octomap   9 #include <octomap/octomap.h> 10 using namespace std; 11  12 int main( int argc, char** argv ) 13 { 14     if (argc != 3) 15     { 16         cout<<"Usage: pcd2octomap <input_file> <output_file>"<<endl; 17         return -1; 18     } 19  20     string input_file = argv[1], output_file = argv[2]; 21     pcl::PointCloud<pcl::PointXYZRGBA> cloud; 22     pcl::io::loadPCDFile<pcl::PointXYZRGBA> ( input_file, cloud ); 23  24     cout<<"point cloud loaded, piont size = "<<cloud.points.size()<<endl; 25  26     //声明octomap变量 27     cout<<"copy data into octomap..."<<endl; 28     // 创建八叉树对象，参数为分辨率，这里设成了0.05 29     octomap::OcTree tree( 0.05 ); 30  31     for (auto p:cloud.points) 32     { 33         // 将点云里的点插入到octomap中 34         tree.updateNode( octomap::point3d(p.x, p.y, p.z), true ); 35     } 36  37     // 更新octomap 38     tree.updateInnerOccupancy(); 39     // 存储octomap 40     tree.writeBinary( output_file ); 41     cout<<"done."<<endl; 42  43     return 0; 44 } 

这个代码是相当直观的。在编译之后，它会产生一个可执行文件，叫做pcd2octomap，放在代码根目录的bin/文件夹下。你可以在代码根目录下这样调：

 1 bin/pcd2octomap data/sample.pcd data/sample.bt 

它会把data文件夹下的sample.pcd（一个示例pcd点云），转换成一个data/sample.bt的octomap文件。你可以比较下pcd点云与octomap的区别。下图是分别调用这些显示命令的结果。

 1 pcl_viewer data/sample.pcd 2 octovis data/sample.ot 

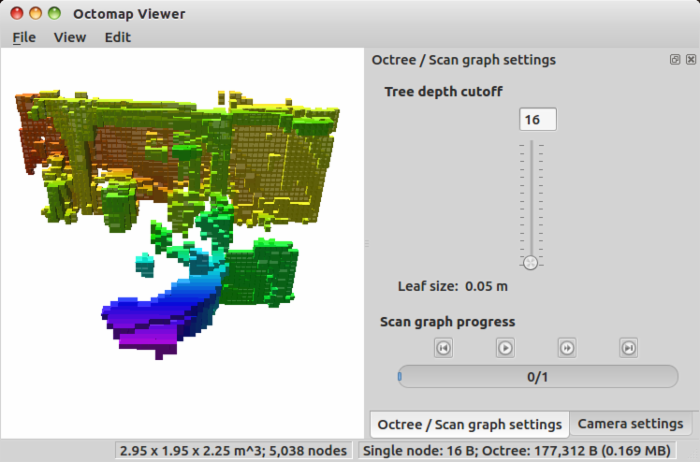
这个octomap里只存储了点的空间信息，而没有颜色信息。我按照高度给它染色了，否则它应该就是灰色的。通过octomap，我们能查看每个小方块是否可以通行，从而实现导航的工作。

以下是对代码的一些注解：

注1：有关如何读取pcd文件，你可以参见pcl官网的tutorial。不过这件事情十分简单，所以我相信你也能直接看懂。

注2：31行采用了C++11标准的for循环，它会让代码看起来稍微简洁一些。如果你的编译器比较老而不支持c++11，你可以自己将它改成传统的for循环的样式。

注3：octomap存储的文件后缀名是.bt（二进制文件）和.ot（普通文件），前者相对更小一些。不过octomap文件普遍都很小，所以也不差这么些容量。如果你存成了其他后缀名，octovis可能认不出来。

例程2：加入色彩信息

第一个示例中，我们将pcd点云转换为octomap。但是pcd点云是有颜色信息的，能否在octomap中也保存颜色信息呢？答案是可以的。octomap提供了ColorOcTree类，能够帮你存储颜色信息。下面我们就来做一个保存颜色信息的示例。代码见：src/pcd2colorOctomap.cpp

  1 #include <iostream>  2 #include <assert.h>  3   4 //pcl  5 #include <pcl/io/pcd_io.h>  6 #include <pcl/point_types.h>  7   8 //octomap   9 #include <octomap/octomap.h> 10 #include <octomap/ColorOcTree.h> 11  12 using namespace std; 13  14 int main( int argc, char** argv ) 15 { 16     if (argc != 3) 17     { 18         cout<<"Usage: pcd2colorOctomap <input_file> <output_file>"<<endl; 19         return -1; 20     } 21  22     string input_file = argv[1], output_file = argv[2]; 23     pcl::PointCloud<pcl::PointXYZRGBA> cloud; 24     pcl::io::loadPCDFile<pcl::PointXYZRGBA> ( input_file, cloud ); 25  26     cout<<"point cloud loaded, piont size = "<<cloud.points.size()<<endl; 27  28     //声明octomap变量 29     cout<<"copy data into octomap..."<<endl; 30     // 创建带颜色的八叉树对象，参数为分辨率，这里设成了0.05 31     octomap::ColorOcTree tree( 0.05 ); 32  33     for (auto p:cloud.points) 34     { 35         // 将点云里的点插入到octomap中 36         tree.updateNode( octomap::point3d(p.x, p.y, p.z), true ); 37     } 38  39     // 设置颜色 40     for (auto p:cloud.points) 41     { 42         tree.integrateNodeColor( p.x, p.y, p.z, p.r, p.g, p.b ); 43     } 44  45     // 更新octomap 46     tree.updateInnerOccupancy(); 47     // 存储octomap, 注意要存成.ot文件而非.bt文件 48     tree.write( output_file ); 49     cout<<"done."<<endl; 50  51     return 0; 52 } 

大部分代码和刚才是一样的，除了把OcTree改成ColorOcTree，以及调用integrateNodeColor来混合颜色之外。这段代码会编译出pcd2colorOctomap这个程序，完成带颜色的转换。不过，后缀名改成了.ot文件。

 1 bin/pcd2colorOctomap data/sample.pcd data/sample.ot 

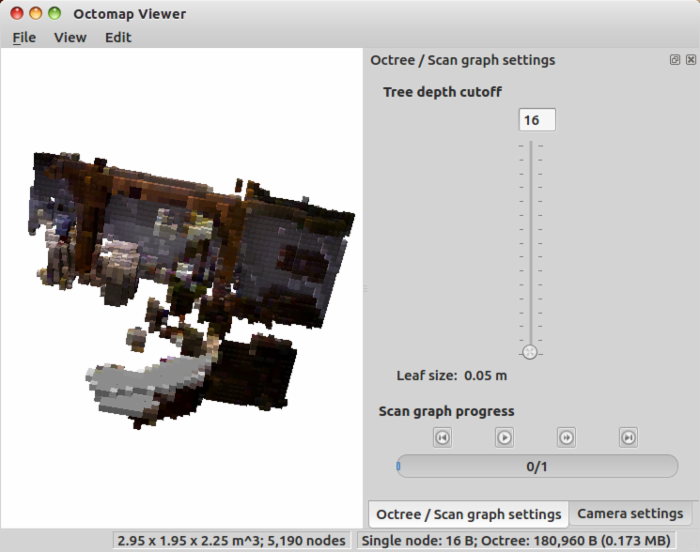
颜色信息能够更好地帮助我们辨认结果是否正确，给予一个直观的印象。是不是好看了一些呢？

例程3：更好的拼接与转换

前两个例程中，我们都是对单个pcd文件进行了处理。实际做slam时，我们需要拼接很多帧的octomap。为了做这样一个示例，我从自己的实验数据中取出了一小段。这一小段总共含有五张图像（因为github并不适合传大量数据），它们存放在data/rgb_index和data/dep_index下。我的slam程序估计了这五个关键帧的位置，放在data/trajectory.txt中。它的格式是：帧编号 x y z qx qy qz qw （位置＋姿态四元数）。事实上它是从一个g2o文件中拷出来的。你可以用g2o_viewer data/result_after.g2o来看整个轨迹。

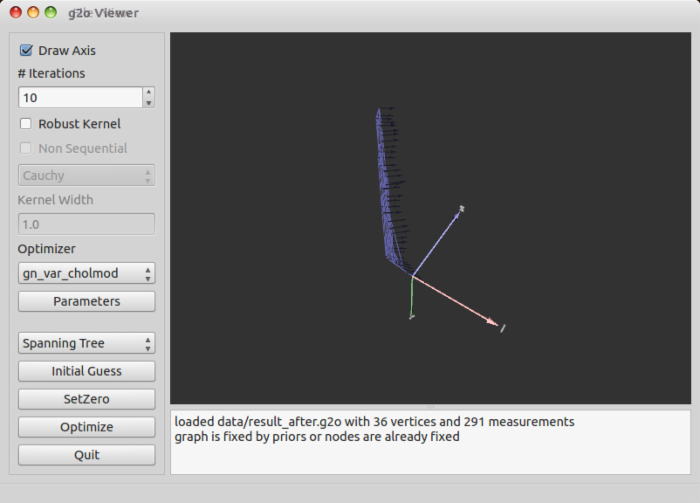
现在我们要做的事，就是根据trajectory.txt里记录的信息，把几个RGBD图拼成一个octomap。这也是所谓的用octomap来建图。我写了一个示例，不知道你能否读懂呢？src/joinMap.cpp

   1 #include <iostream>   2 #include <vector>   3    4 // octomap    5 #include <octomap/octomap.h>   6 #include <octomap/ColorOcTree.h>   7 #include <octomap/math/Pose6D.h>   8    9 // opencv 用于图像数据读取与处理  10 #include <opencv2/core/core.hpp>  11 #include <opencv2/imgproc/imgproc.hpp>  12 #include <opencv2/highgui/highgui.hpp>  13   14 // 使用Eigen的Geometry模块处理3d运动  15 #include <Eigen/Core>  16 #include <Eigen/Geometry>   17   18 // pcl  19 #include <pcl/common/transforms.h>  20 #include <pcl/point_types.h>  21   22 // boost.format 字符串处理  23 #include <boost/format.hpp>  24   25 using namespace std;  26   27 // 全局变量：相机矩阵  28 // 更好的写法是存到参数文件中，但为方便起见我就直接这样做了  29 float camera_scale  = 1000;  30 float camera_cx     = 325.5;  31 float camera_cy     = 253.5;  32 float camera_fx     = 518.0;  33 float camera_fy     = 519.0;  34   35 int main( int argc, char** argv )  36 {  37     // 读关键帧编号  38     ifstream fin( "./data/keyframe.txt" );  39     vector<int> keyframes;  40     vector< Eigen::Isometry3d > poses;  41     // 把文件 ./data/keyframe.txt 里的数据读取到vector中  42     while( fin.peek() != EOF )  43     {  44         int index_keyframe;  45         fin>>index_keyframe;  46         if (fin.fail()) break;  47         keyframes.push_back( index_keyframe );  48     }  49     fin.close();  50   51     cout<<"load total "<<keyframes.size()<<" keyframes. "<<endl;  52   53     // 读关键帧姿态  54     // 我的代码中使用了Eigen来存储姿态，类似的，也可以用octomath::Pose6D来做这件事  55     fin.open( "./data/trajectory.txt" );  56     while( fin.peek() != EOF )  57     {  58         int index_keyframe;  59         float data[7]; // 三个位置加一个姿态四元数x,y,z, w,ux,uy,uz  60         fin>>index_keyframe;  61         for ( int i=0; i<7; i++ )  62         {  63             fin>>data[i];  64             cout<<data[i]<<" ";  65         }  66         cout<<endl;  67         if (fin.fail()) break;  68         // 注意这里的顺序。g2o文件四元数按 qx, qy, qz, qw来存  69         // 但Eigen初始化按照qw, qx, qy, qz来做  70         Eigen::Quaterniond q( data[6], data[3], data[4], data[5] );  71         Eigen::Isometry3d t(q);  72         t(0,3) = data[0]; t(1,3) = data[1]; t(2,3) = data[2];  73         poses.push_back( t );  74     }  75     fin.close();  76   77     // 拼合全局地图  78     octomap::ColorOcTree tree( 0.05 ); //全局map  79   80     // 注意我们的做法是先把图像转换至pcl的点云，进行姿态变换，最后存储成octomap  81     // 因为octomap的颜色信息不是特别方便处理，所以采用了这种迂回的方式  82     // 所以，如果不考虑颜色，那不必转成pcl点云，而可以直接使用octomap::Pointcloud结构  83       84     for ( size_t i=0; i<keyframes.size(); i++ )  85     {  86         pcl::PointCloud<pcl::PointXYZRGBA> cloud;   87         cout<<"converting "<<i<<"th keyframe ..." <<endl;  88         int k = keyframes[i];  89         Eigen::Isometry3d& pose = poses[i];  90   91         // 生成第k帧的点云，拼接至全局octomap上  92         boost::format fmt ("./data/rgb_index/%d.ppm" );  93         cv::Mat rgb = cv::imread( (fmt % k).str().c_str() );  94         fmt = boost::format("./data/dep_index/%d.pgm" );  95         cv::Mat depth = cv::imread( (fmt % k).str().c_str(), -1 );  96   97         // 从rgb, depth生成点云，运算方法见《一起做》第二讲  98         // 第一次遍历用于生成空间点云  99         for ( int m=0; m<depth.rows; m++ ) 100             for ( int n=0; n<depth.cols; n++ ) 101             { 102                 ushort d = depth.ptr<ushort> (m) [n]; 103                 if (d == 0) 104                     continue; 105                 float z = float(d) / camera_scale; 106                 float x = (n - camera_cx) * z / camera_fx; 107                 float y = (m - camera_cy) * z / camera_fy; 108                 pcl::PointXYZRGBA p; 109                 p.x = x; p.y = y; p.z = z; 110  111                 uchar* rgbdata = &rgb.ptr<uchar>(m)[n*3]; 112                 uchar b = rgbdata[0]; 113                 uchar g = rgbdata[1]; 114                 uchar r = rgbdata[2]; 115  116                 p.r = r; p.g = g; p.b = b; 117                 cloud.points.push_back( p );  118             } 119         // 将cloud旋转之后插入全局地图 120         pcl::PointCloud<pcl::PointXYZRGBA>::Ptr temp( new pcl::PointCloud<pcl::PointXYZRGBA>() ); 121         pcl::transformPointCloud( cloud, *temp, pose.matrix() ); 122  123         octomap::Pointcloud cloud_octo; 124         for (auto p:temp->points) 125             cloud_octo.push_back( p.x, p.y, p.z ); 126          127         tree.insertPointCloud( cloud_octo,  128                 octomap::point3d( pose(0,3), pose(1,3), pose(2,3) ) ); 129  130         for (auto p:temp->points) 131             tree.integrateNodeColor( p.x, p.y, p.z, p.r, p.g, p.b ); 132     } 133      134     tree.updateInnerOccupancy(); 135     tree.write( "./data/map.ot" ); 136  137     cout<<"done."<<endl; 138      139     return 0; 140  141 } 

大部分需要解释的地方，我都在程序里写了注解。我用了一种稍微有些迂回的方式：先把图像转成pcl的点云，变换后再放到octotree中。这种做法的原因是比较便于处理颜色，因为我希望做出带有颜色的地图。如果你不关心颜色，完全可以不用pcl，直接用octomap自带的octomap::pointcloud来完成这件事。

insertPointCloud会比单纯的插入点更好一些。octomap里的pointcloud是一种射线的形式，只有末端才存在被占据的点，中途的点则是没被占据的。这会使一些重叠地方处理的更好。

最后，五帧数据拼接出来的点云大概长这样：

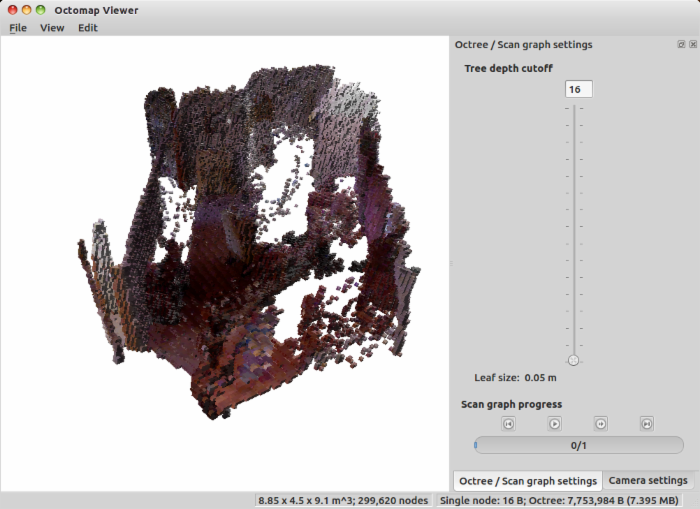
可能并不是特别完整，毕竟我们只用了五张图。这些数据来自于nyud数据集的dining_room序列，一个比较完整的图应该是这样的：

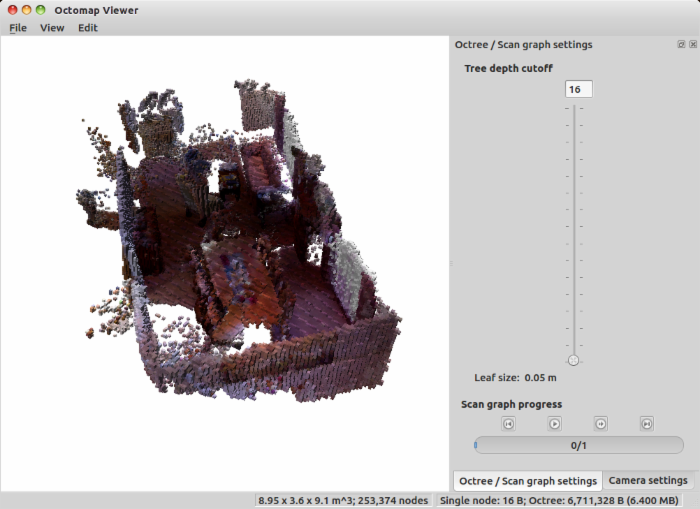
至少是比纯粹点云好些了吧？好了，关于例程就介绍到这里。如果你准备使用octomap，这仅仅是个入门。你需要去查看它的文档，了解它的类结构，以及一些重要类的使用、实现方式。

《SLAM拾萃》第一讲，octomap，就为大家介绍到这里啦。最近我发现自己写东西，讲东西都越来越长，所以请原谅我越来越啰嗦的写作和说话风格。希望它能帮助你！我们下讲再见！

如果你觉得我的博客有帮助，可以进行几块钱的小额赞助，帮助我把博客写得更好。（虽然我也是从别处学来的这招……）

小萝卜：师兄你学坏了啊！

参考文献

[1]. OctoMap: An efficient probabilistic 3D mapping framework based on octrees, Hornung, Armin and Wurm, Kai M and Bennewitz, Maren and Stachniss, Cyrill and Burgard, Wolfram, Autonomous Robots, 2013.

[2]. OctoMap: A probabilistic, flexible, and compact 3D map representation for robotic systems, Wurm, Kai M and Hornung, Armin and Bennewitz, Maren and Stachniss, Cyrill and Burgard, Wolfram, ICRA 2010.