转载

数学模型的其他应用

数学技术之模型篇（5）

三、围棋中的数学模型

围棋，一种中国古代发明、两人进行智力游戏性很强的棋类，有黑白、手谈等诸多名字，为琴棋书画的四艺之一。围棋流行于亚太，覆盖世界范围，是一种非常流行的棋类，被认为是世界上一种最复杂的棋类游戏。对围棋曾有《棋定天下》一诗赞道：

无声无息起硝烟，黑白参差云雨颠。

凝目搜囊巧谋略，全神贯注暗周旋。

山穷水尽无舟舸，路转峰回别样天。

方寸之间人世梦，三思落子亦欣然。

围棋使用方形格状棋盘及黑白二色圆形棋子进行对弈，棋盘上有纵横各19条直线将棋盘分成361个交叉点，棋子走在交叉点上，双方交替行棋，落子后不能移动，以围地多者为胜。由于它将科学、艺术和竞技三者融为一体，有着发展智力、培养意志和机动灵活的战略战术思想意识的特点，因而，几千年来长盛不衰，并逐渐地发展成了一种国际性的文化竞技活动。

围棋棋盘之一（取自互联网）

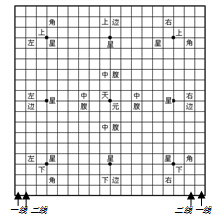
围棋棋盘之二（取自互联网）

自围棋问世以来，随着人们对其认识的不断深入，棋盘和下棋规则也在不断的变化中走向完善。现在的围棋棋盘由纵横交错的十九条直线组成的361个方形交叉点组成。如上图“围棋棋盘之二”所示，棋盘有上、下、左、右四条边，标着八星和中天元九个点，分为边、角和中腹等不同的区域。我们把四条边界线称为一线，与边界线相邻的四条线称为二线，并依次根据它们与边界的距离远近分别称为三线、四线等等。各线上的点由于距离边界相同，使它们具有比较一致的特性。

下围棋时，先手可率先抢占有利点，造成下棋的不公平。围棋棋盘要多大，先手应该为后手贴多少目棋，是影响下棋公平的主要因素。经过近4000年左右的多次变化，围棋棋盘由古时每边十一道增至现在的十九道，胜负贴目也已基本定论并被广泛接受，但至今仍还缺乏一个令人信服的证明，说明其合理性。现在要问，能否对围棋构造一个数学模型，证明其合理性呢？结合当今围棋规则，用数学建模的方法观察，分析，计算出相关数据，看其是否合理、可用，目的是为了尽可能的使弈棋的公平，使棋手的水平充分发挥。

在围棋中，人们比较看重的问题有两个：① 围棋棋盘经历了多次变化，围棋的棋盘道数多少才最为合理？② 在最为合理的道数下，先手应该贴后手多少目，有没有可能使贴目接近于0？下面谈谈如何构建数学模型来解决这些问题。限于篇幅，这里只讨论第一个问题。

为对围棋构建可用的数学模型并解决上述问题，作如下假设：① 对弈双方棋力相当；② 棋盘连续，棋手可在棋盘任意点线的空白处布子；③ 棋类比赛，有攻有守，攻守成败以最后成活与占地多少为准；④ 对于一块含两个以上眼位的成活棋块，以其棋子数除以这些棋子所包含的目数得到的商值称为此棋块的 “目效率” ，记为PE。

弈棋的不公平主要来自于先手，如果改掉规则，让两人同时落子，便不存在不公平的问题。但现实是总有先后手之分，自然先手会用第一步占据棋盘上最有利的点，围棋棋盘除天元外，所有的点都四点对称。所以，只要天元不是最有利的点，那么最有利的点就有4个，成对出现，后手的损失就不会太大。所以问题就转化为在什么情况下，天元不会成为最有利的位置。

当棋盘过小时，天元的位置极其重要，对于总道数少的小棋盘甚至第一步走在天元位置上就可以赢得全局，但随着棋盘道数的不断增加，棋盘增大，天元的优势就不明显了，原因是天元对边角的控制不足，导致边角的利益大于天元的利益，问题转化为当道数为多少时，边角可摆脱天元对边角的控制。为使围棋对弈时先、后手差异不太大，我们不妨取中腹和边域目效率相差不大为目标和依据，看看围棋的道数取多少为好。

假设棋盘每边的边数为x道（显然，x应为正整数），现在棋盘的道数x=19。为实战需要，围棋棋盘的道数不能太大，也不能太小，不妨假设11≤x≤23。将第四边上的八星连线，所围之地称为中腹，占有目数(x-8) ² ，记其目效率为PE ₄ ；将第3边连线，1-2边组成边域, 占有目数8x-16，记其目效率为PE ₃ 。由于对x的限制，三线外的边域及四线围成的中腹区域都已成为实空，对手无法再做活。这时，边和中腹区域的目效率分别为：

PE ₃ = (8x-16)/(4x-20) ， PE ₄ = (x-8) ² /(4x-28)。

中腹和边域目效率之差为

E(x) = PE ₄ – PE ₃ = (x-8) ² /(4x-28) – (8x-16)/(4x-20)

基于E(x)为一单调增函数，且E(18)= -0.18881和E(19)= 0.09222，故0解应在开区间（18,19）之中，其有效解道数应取为正整数，由│E(19)│<│E(18)│，说明围棋棋盘道数x应为取为19，取19×19的围棋棋盘是最佳的，因而说明现在的围棋棋盘取19道有其一定的合理性。

四、自然灾害预测模型

对地震、森林火灾等自然灾害，以及飞机飞行失事、考试临场发挥失常等各种被认为仅具偶然性的随机事件，过去利用“响铃曲线”数学模型来预测它们发生的可能性大小或概率，因其形状类似于铃铛而得名。最新研究出来的数学曲线，它的形状较之“响铃模型”更宽一些，曲线弧度较小而显得较为平滑，更能准确地表示那些最罕见的随机事件的发生概率，要比老曲线模型所预测的更加频繁。新的曲线模型，凝聚了雪崩、地震等自然灾害及生态系统中物种分布等各个领域预测专家的共同智慧和创意，有着更为普遍的适用性和更高的拟合度。

最新预测曲线是偶然性紊乱现象研究“浑沌理论”领域的一大突破，对人类社会的工程、气象、灾害、保险、生态等各个专业行业单个随机性突发、偶发事件的具体预测，具有极为重要的实际价值，揭示出了一个更为精确的数学曲线模型，为今后解释和预测人类社会及自然界各种随机偶发性事件的发生规律，提供了更为有效的科学手段。

五、语音识别中的数学模型

计算机语音自动识别就是让计算机能听懂人说话，实现人类自然语言和计算机机器语言之间的交流。这一问题曾经被认为是“比登月还难”的科学问题。

（取自互联网）

计算机语音识别是一个模式识别匹配的过程。在这个过程中，计算机首先要根据人的语音特点建立语音模型，对输入的语音信号进行分析，并抽取所需的特征，在此基础上建立语音识别所需的模板。计算机在识别过程中，根据语音识别的整体模型，将计算机中存放的语音模板与输入的语音信号的特征进行比较，根据一定的搜索和匹配策略，找出一系列最优的与输入的语音匹配的模板。然后，据此模板的定义，通过查表就可以给出计算机的识别结果。显然，这种最优的结果与特征的选择、语音模型和语言模型的好坏、模板是否准确等都有着直接的关系。

计算机自动语音识别用途广泛，潜力巨大，但要真正实现人与计算机的自然交流却很难，它不仅需要高深的基础理论的突破和巨型计算机，更需要建有使用方便、高效可靠的数学模型。

一个语音识别系统性能好坏的关键首先是它所采用的语音模型能否真实地反映话音的物理变化规律，所用的语言模型能否表达自然语言所包含的丰富语言学知识。但在实际应用中，无论是语音信号还是人类的自然语言都是随机、多变和不稳定的，很难把握。这就是目前语音识别过程中的最大难点。

制约语音识别技术发展的根本是语音识别依据的模型和算法，模型和算法是计算机描述语音的能力能否抓住人的语音的本质的关键。

目前，在研发语音识别系统时常用的算法有基于神经网络的训练和识别算法、基于动态时间归整匹配的识别算法和基于统计的隐含马尔可夫模型（Hidden Markov Model，简记为HMM）识别和训练算法等。

隐含马尔可夫法(HMM)是70年代引入语音识别理论的，它的出现使得自然语音识别系统取得了实质性的突破。HMM方法现已成为语音识别的主流技术，目前大多数大词汇量、连续语音的非特定人语音识别系统都是基于HMM模型的。HMM是对语音信号的时间序列结构建立统计模型，将之看作一个数学上的双重随机过程：一个是用具有有限状态数的马尔科夫链来模拟语音信号统计特性变化的隐含的随机过程，另一个是与马尔科夫链的每一个状态相关联的观测序列的随机过程。前者通过后者表现出来，但前者的具体参数是不可测的。人的言语过程实际上就是一个双重随机过程，语音信号本身是一个可观测的时变序列，是由大脑根据语法知识和言语需要(不可观测的状态)发出的音素的参数流。可见HMM合理地模仿了这一过程，很好地描述了语音信号的整体非平稳性和局部平稳性,是较为理想的一种语音模型。

基于统计的HMM算法可能是目前最为成功的一种语音识别模型和算法。目前所能见到的各种性能优良的连续语音识别系统几乎无一例外地采用了这种模型。由于这种数学模型出现的时间较早，人们对它的研究也比较深入，已建立起了完整的理论框架。从20世纪80年代初人们开始用这种模型来描述语音信号后，就不断对它进行各种改进和发展。HMM的算法是将语音看成是一连串特定状态，这种状态是不能被直接观测到的，是以某种隐含的关系与语音的观测量或特征相关联。这种隐含关系在HMM模型中通常以概率形式表现出来，模型的输出结果也以概率形式给出。这为系统最后给出一个稳健的判决创造了条件。

如今，各种形式的HMM模型和算法虽已日趋成熟，但在一些重要方面还存在着许多不足之处，如：

①经典HMM是一个齐次马尔可夫模型，状态转移概率与状态驻留长度无关，这与语音的实际情况不符；

②经典HMM模型训练算法和识别算法都是假设语音特征是相互独立的，这和语音信号的实际情况也不符；

③经典HMM模型用于大词汇表的识别系统时，模型训练量过大，甚至是灾难性的，存储量也过大，很难应用。

对HMM模型在语音识别应用中存在的问题的进一步研究和改进，得到了一个基于段长分布的非齐次隐含马尔可夫模型（Duration Distribution Based Hidden Markov Model，简记为DDBHMM）。这一模型用状态的段长分布函数替代齐次HMM中的状态转移矩阵，抛弃了“平稳性假设”，从非平稳的角度考虑问题，使模型成为一种基于状态段长分布的隐含马尔可夫模型。段长分布函数的引入解决了经典HMM语音识别模型的许多矛盾。

人工神经网络(ANN)方法是二十世纪80年代末期提出的一种新的语音识别方法。人工神经网络本质上是一个自适应非线性动力学系统，模拟了人类神经活动的原理，具有自适应性、并行性、稳健性、容错性和学习特性，其强的分类能力和输入-输出映射能力在语音识别中很有吸引力。但由于存在训练、识别时间太长的缺点，目前仍处于实验探索阶段。由于ANN不能很好的描述语音信号的时间动态特性，所以常把ANN与传统识别方法结合，分别利用各自优点来进行语音识别。

就算法模型而言，制约语音识别技术发展的根本是语音识别依据的模型和算法，需要进一步的突破。目前能看出它的一些明显不足，尤其在中文语音识别方面，语言模型还有待完善，因为语言模型和声学模型正是听写识别的基础，这方面没有突破，语音识别的进展就只能是一句空话。目前使用的语言模型只是一种概率模型，还没有用到以语言学为基础的文法模型，而要使计算机真正理解人类的语言，就必须在这方面取得进展，这是一个相当艰苦的工作。此外，随着计算机硬件资源的不断发展，一些核心算法如特征提取、搜索算法或者自适应算法将有可能进一步改进。可以相信，计算机硬件和软件技术的共同进步将为语音识别技术的基础性工作带来福音。

正文到此结束