将每个时间步的图降维为点：动态网络可视化探索分析方法 (Reducing Snapshots to Points: A Visua...
目前，动态图可视分析方法主要分为small multiples和animation两大类。Small multiples方法，将时间映射到空间上，用户需要同时观察若干个snapshot，相互比较来获取差异。由于屏幕空间有限，当时间步很多时，很难同时展示出所有时刻的网络，且用户难以分析获取动态网络的变化模式。Animation方法，将时间映射到时间维度，用户在每个时刻只能观察到一个时间步的网络，需要去记忆，理解时间步之间网络的变化情况，进而理解动态图的变化模式。
本文提出一种新颖的方法，来分析动态图的变化模式。他们将每个时间步的网络转换成高维向量，将这些高维向量投影到二维平面，用点表示。如图1所示，投影后得到的布局中，每个点表示一个时间步的snapshot， 每条边连接了两个相邻时刻的顶点。这个方法可以有效地帮助用户探索分析动态图的稳定状态、重现状态、异常状态以及状态与状态之间的转移过程。
图1 将左图的snapshot降维到二维平面的点，如右图所示
这个方法包括四个步骤（图2）：
图2 流程图
1） 离散化（Discretization）：原始数据由一系列的事件组成，每个事件均发生在两个实体之间。为了将原始数据离散化，构造一系列的snapshot。他们采用滑动窗口在事件序列上滑动的方法，生成一系列的时间窗（为了最后投影结果的连续性，建议时间窗之间的重叠率为50%以上），然后将每个时间窗内的所有事件转换成一个等价的网络。网络中的顶点和边分别是这个时间窗内出现的顶点和边，其中边的权重表示该边在这个时间窗出现的次数。图3展示了，不同重叠率，对投影结果的影响。观察可发现，重叠率越高，越多有趣的模式会展示出来。
图3 滑动窗口，不同重叠率对投影结果的影响。第一行，滑动窗口大小可变，每个窗口包含的顶点数恒定；第二行，滑动窗口大小恒定，每个窗口包含的顶点数可变。
2） 向量化和归一化（Vectorization and Normalization）：为了进行投影，需要将每个snapshot转化成一个高维向量。具体的做法是，先用邻接矩阵表示每个时间步的网络，然后将n*n的矩阵，转化为1*n的高维向量，也可在高维向量中添加一些额外的属性，比如活跃顶点的个数等。文章讨论了二值化，Min-max scaling，z-score归一化方法对最后投影结果的影响。如图4所示，z-score归一化方法不会压抑网络中的异常现象，相较而言，是比较好的选择。但是否需要进行归一化，选择哪种归一化方法，还是需要根据具体的数据来定。
图4 未归一化和采用不同归一化方法，线性投影获得的结果
3） 投影（Dimensionality Reduction）：将高维向量采用线性投影方法（PCA）或非线性投影方法（MDS 和t-SNE）进行投影，获取二维投影结果。文章讨论了不同的投影方法，不同的距离方法对结果的影响。他们认为没有一种标准来说明何种方法更好，具体的投影方法，用户需要根据具体的数据进行选择。
4） 可视化与设计（Visualization and Interaction）：图5展示了系统的界面。
图5 系统界面。A，投影图 ( Projection View)，每个点表示一个snapshot，颜色表示时间；B，图布局 (Network View)，采用点边形式展示在A视图中选中的snapshot的细节；C， 时间轴 (Time Control)；D，辅助视图 (Auxiliary View) ，展示在A视图中选择的snapshot的度的分布等信息。
文章介绍了他们方法在虚拟数据和真实数据上的使用情况。
Case1–虚拟数据（图6、图7）：
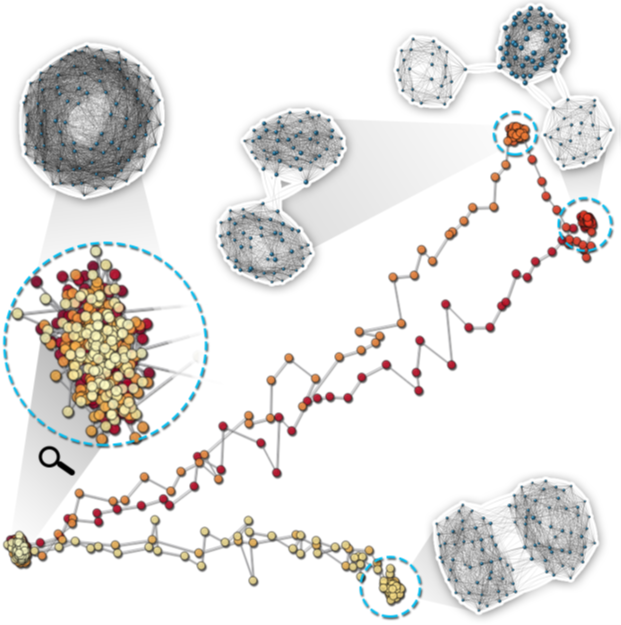
图6 线性PCA投影结果
图7 (a) 选择时间维度为x轴，PCA降维的第一主成分为y轴，绘制的布局；(b) 采用非线性降维方法获得的结果
在这个例子中，作者们生成了一个包含100个顶点，9900条边和900个时间步的虚拟网络。图6、图7中，颜色由浅到深表示时间的推移。图6是采用PCA方法投影得到的布局，清晰的展现出四个稳定状态，一个重现状态和五个过渡状态。图7（a）展示的是将时间轴作为横轴的PCA投影结果，可以清晰的看到四个不同的稳定状态，且最下方的稳定状态出现了三次；图7（b）是采用非线性投影方法获取的结果，四个不同的稳定状态可以很好地被区分，但是，稳定态之间的转移过程没有展示出来。
Case2 – 真实数据（图8、图9、图10）：
在这个例子中使用的数据，记录了一个学校五个不同班共180个学生为期7个工作日的面对面交流数据，一共有45047条记录。预处理后，得到的动态图网络中共有180个顶点，10104条边，2015个snapshot。
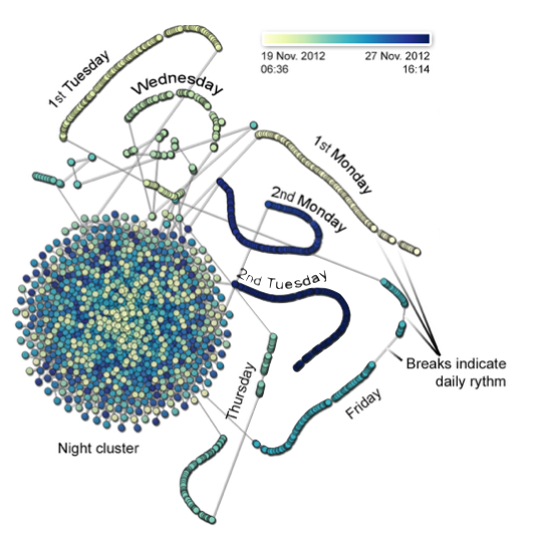
图8 非线性降维方法结果。不同的颜色表示不同的天，从浅到深，映射周一到下周二的时间信息。
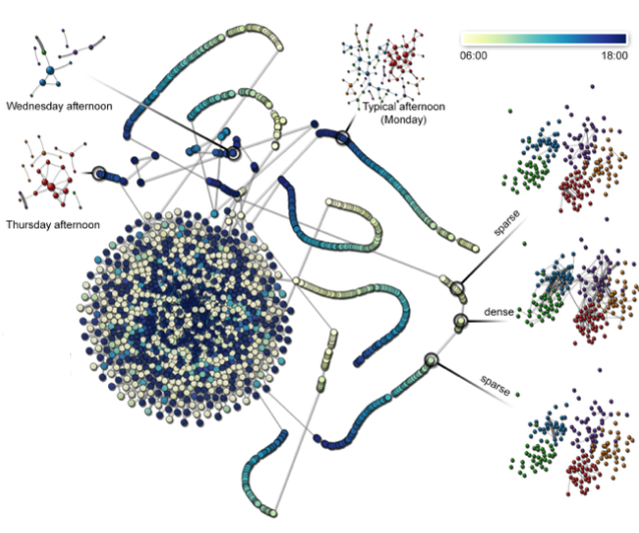
图9 非线性降维结果。颜色表示不同的时间，从浅到深，映射早上6点到下午6点的时间。
图8、图9展示的是采用非线性投影方法获得的结果。两幅图的不同在于颜色编码方法不一样。图8编码的是从19日到27日；图9编码的是每天早上6点到晚上6点。从图8，我们可以发现每个工作日基本上都是连续的一条轨迹，其中每天都会在几个基本固定的时刻断开，作者们分析，这是因为上课，午休等导致的。从图9，可以发现周三下午有异常，当天点的分布不连续，这是因为周三下午有一场考试导致的。
图10 横轴映射时间信息，从周一到下周二；纵轴是PCA降维的第一主成分；颜色映射了早上6点到下午6点的时间信息。
图10展示的是在PCA投影中，将横轴替换为时间轴的结果。从图10，可以看到七个工作日网络的规律性变化。早上开始逐渐变的活跃，中午活跃度降低，下午又开始活跃，直到晚上恢复完全的平静。而周六周日，因为没有数据，都处于平静状态。
这篇文章是2015 VIS 的 Best Paper。文章提出的想法以及采用的方法并不复杂，但效果很不错。
1） 将每个时间步的网络看成高维的顶点，将其投影到二维平面，进而分析每个时间步，网络的相似性。这个方法可以有效的帮助用户分析探索动态图中的稳定状态，重现状态，异常状态以及状态与状态之间的转移情况。
2） 文章的一个特色是，对方法中可能的情况进行了充分细致的讨论，比如离散化中时间窗重叠率，归一化中归一化方法对投影结果的影响，投影中不同投影方法，距离度量方法。
3） 在虚拟数据和真实数据上讨论说明方法的有效性。虚拟数据的结果更为漂亮，吸引人，从理论上说明了方法的可用性；真实数据上的分析，进一步证明了方法的实用性。
动态图的可视分析，因为时间步长，每个时间步顶点多，边密集，挑战较大。传统的Small Multiples 和Animation方法，都不能很好地协助用户分析网络的变化情况。将每个时间步的snapshot转化为二维平面的顶点，通过分析二维平面上，顶点之间的远近，来分析snapshot之间的相似程度，进而分析网络的变化模式。从宏观的角度分析大型网络的变化模式，是个很好的切入点。
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
