转载

【模式匹配】KMP算法的来龙去脉

1. 引言

字符串匹配是极为常见的一种模式匹配。简单地说，就是判断主串 /(T/) 中是否出现该模式串 /(P/) ，即 /(P/) 为 /(T/) 的子串。特别地，定义主串为 /(T[0 /dots n-1]/) ，模式串为 /(P[0 /dots p-1]/) ，则主串与模式串的长度各为 /(n/) 与 /(p/) 。

2. 匹配算法

先介绍暴力（brute-force）匹配的方法，然后根据暴力方法的缺点而引出KMP算法的思想，接着介绍如何计算部分匹配函数（Partial Match）与next函数的计算。

暴力方法

暴力匹配方法的思想非常朴素：

依次从主串的首字符开始，与模式串逐一进行匹配；
遇到失配时，则移到主串的第二个字符，将其与模式串首字符比较，逐一进行匹配；
重复上述步骤，直至能匹配上，或剩下主串的长度不足以进行匹配。

下图给出了暴力匹配的例子，主串 T="ababcabcacbab" ，模式串 P="abcac" ，第一次匹配：

【模式匹配】KMP算法的来龙去脉

第二次匹配：

第三次匹配：

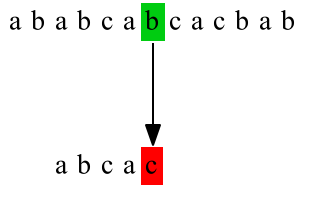
C代码实现：

int brute_force_match(char *t, char *p) {     int i, j, tem;     int tlen = strlen(t), plen = strlen(p);     for(i = 0, j = 0; i <= tlen - plen; i++, j = 0) {         tem = i;         while(t[tem] == p[j] & j < plen) {             tem++;             j++;         }         // matched         if(j == plen) {             return i;         }     }     // [p] is not a substring of [t]     return -1; }

时间复杂度： i 在主串移动次数（外层的for循环）有 /(n-p/) 次，在失配时 j 移动次数最多有 /(p-1/) 次（最坏情况下）；因此，复杂度为 /(O(n*p)/) 。

我们仔细观察暴力匹配方法，发现：失配后下一次匹配，

主串的起始位置 = 上一轮匹配的起始位置 + 1；
模式串的起始位置 = 首字符 P[0] 。

如此未能利用已经匹配上的字符的信息，就造成了 重复匹配 。举个例子，比如：第一次匹配失败时，主串、模式串失配位置的字符分别为 a 与 c ，下一次匹配时主串、模式串的起始位置分别为 T[1] 与 P[0] ；因为在模式串中 c 之前是 ab ，未有 重复的字符结构 ，因此 T[1] 与 P[0] 肯定不能匹配上，这样造成了重复匹配。直观上，下一次的匹配应从 T[2] 与 P[0] 开始。

KMP思想

首先，来看第一次匹配失败，如下图所示：

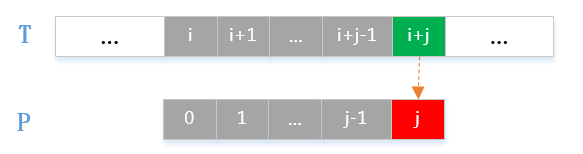
从图中可以看出，已匹配上的字符满足：

/[ T[i /dots i+j-1] = P[0 /dots j-1] /]

KMP算法思想：利用已经匹配上的字符信息，在下一次的匹配时，将已经匹配上的字符结构重新对齐，置下一次匹配

主串的起始位置 = 上一轮匹配的失配位置；
模式串的起始位置 = 重复字符结构的下一位字符

如下图所示：

从图中得到模式串的重复字符结构：

/begin{equation}

T[i+j-m-1 /dots i+j-1] = P[j-m-1 /dots j-1] = P[0 /dots m]

/label{eq:overlap}

/end{equation}

且有

/[ T[i+j] /neq P[j] /neq P[m+1] /]

那么应如何选取 /(m/) 值呢？假定有满足式子/eqref{eq:overlap}的两个值 /(m_1 > m_2/) ，如下图所示：

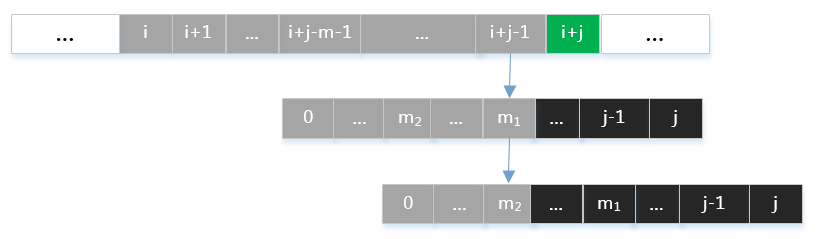
如果选取 /(m=m_2/) ，则会丢失 /(m=m_1/) 的这一种字符匹配情况。由数学归纳法容易知道， /(m/) 值应为满足式子/eqref{eq:overlap}中最大的那一个。

模式串 P="abcac" 匹配主串 T="ababcabcacbab" 的KMP过程如下图：

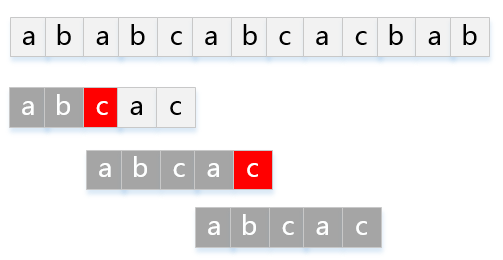
部分匹配函数

根据上面的讨论，我们定义部分匹配函数（Partial Match，在数据结构书[2]称之为失配函数）：

/[ f(j) = /left/{ {/matrix{ {/max /{ m /} } & P[0/dots m]=P[{j-m}/dots {j}],0/le m < j /cr {-1} & else /cr } } /right. /]

失配函数表示模式串中重复字符结构信息。KMP中大名鼎鼎的 next[j] 函数表示对于模式串失配位置为 j+1 ，下一轮匹配时模式串的起始位置（即对齐于主串的失配位置）；则有

/[ next[j] = f(j)+1 /]

如何计算部分匹配函数呢？首先来看一个例子，模式串 P="ababababca" 的部分匹配函数与next函数如下：

j	0	1	2	3	4	5	6	7	8	9
P[j]	a	b	a	b	a	b	a	b	c	a
f(j)	-1	-1	0	1	2	3	4	5	-1	0
next[j]	0	0	1	2	3	4	5	6	0	1

模式串的 f(j) 满足 /(P[0 /dots f(j)]=P[j-f(j) /dots j]/) ，在计算 f(j+1) 分为两类情况：

若 /(P[j+1]=P[f(j)+1]/) ，则有 /(P[0 /dots f(j)+1]=P[j-f(j) /dots j+1]/) ，因此 f(j+1)=f(j)+1 。
若 /(P[j+1] /neq P[f(j)+1]/) ，则要从 /(P[0 /dots f(j)]/) 中找出满足 P[f(j+1)]=P[j+1] 的 f(j+1) ，从而得到 /(P[0 /dots f(j+1)]=P[j+1-f(j+1) /dots j+1]/)

其中，根据 f(j) 的定义有：

/[ P[j]=P[f(j)]=P[f(f(j))]=/cdots = P[f^k(j)] /]

其中， /(f^k(j)=f(f^{k-1}(j))/) 。通过上面的例子可知，函数 /(f^k(j)/) 是随着 /(k/) 递减的，并最后收敛于 -1 。此外， P[j] 与 p[j+1] 相邻；因此若存在 P[f(j+1)]=P[j+1] ，则必有

/[ f(j+1)=f^k(j)+1 /]

为了求满足条件的最大的 f(j+1) ，因 /(f^k(j)/) 是随着 /(k/) 递减的，故应求满足上式的最小 /(k/) 值。

总结部分匹配函数的计算分析如下：

/[ f(j) = /left/{ {/matrix{ {f^k(j-1)+1} & /min /limits_{k} P[f^k(j-1)+1]=P[j] /cr {-1} & else /cr } } /right. /]

代码实现

部分匹配函数（失配函数）的C实现代码：

int *fail(char *p) {     int len = strlen(p);     int *f = (int *) malloc(len * sizeof(int));     f[0] = -1;     int i, j;     for(j = 1; j < len; j++) {         for(i = f[j-1]; ; i = f[i]) {             if(p[j] == p[i+1]) {                 f[j] = i + 1;                 break;             }             else if(i == -1) {                 f[j] = -1;                 break;             }         }     }     return f; }

KMP的C实现代码：

int kmp(char *t, char *p) {     int *f = fail(p);     int i, j;     for(i = 0, j = 0; i < strlen(t) && j < strlen(p); ) {         if(t[i] == p[j]) {             i++;             j++;         }         else if(j == 0)             i++;         else             j = f[j-1] + 1;     }     return j == strlen(p) ? i - strlen(p) : -1; }