转载

面试常见十大类算法汇总

标签：面试算法 | 发表时间：2016-01-06 01:19 | 作者：

出处：http://www.iteye.com

1.String/Array/Matrix

在Java中，String是一个包含char数组和其它字段、方法的类。如果没有IDE自动完成代码，下面这个方法大家应该记住：

toCharArray() //get char array of a String Arrays.sort()  //sort an array Arrays.toString(char[] a) //convert to string charAt(int x) //get a char at the specific index length() //string length length //array size  substring(int beginIndex)  substring(int beginIndex, int endIndex) Integer.valueOf()//string to integer String.valueOf()/integer to string

String/arrays很容易理解，但与它们有关的问题常常需要高级的算法去解决，例如动态编程、递归等。

下面列出一些需要高级算法才能解决的经典问题：

Evaluate Reverse Polish Notation
Longest Palindromic Substring
单词分割
字梯
Median of Two Sorted Arrays
正则表达式匹配
合并间隔
插入间隔
Two Sum
3Sum
4Sum
3Sum Closest
String to Integer
合并排序数组
Valid Parentheses
实现strStr()
Set Matrix Zeroes
搜索插入位置
Longest Consecutive Sequence
Valid Palindrome
螺旋矩阵
搜索一个二维矩阵
旋转图像
三角形
Distinct Subsequences Total
Maximum Subarray
删除重复的排序数组
删除重复的排序数组2
查找没有重复的最长子串
包含两个独特字符的最长子串
Palindrome Partitioning

2.链表

在Java中实现链表是非常简单的，每个节点都有一个值，然后把它链接到下一个节点。

class Node {  int val;  Node next;    Node(int x) {   val = x;   next = null;  } }

比较流行的两个链表例子就是栈和队列。

栈（Stack）

class Stack{  Node top;     public Node peek(){   if(top != null){    return top;   }     return null;  }    public Node pop(){   if(top == null){    return null;   }else{    Node temp = new Node(top.val);    top = top.next;    return temp;    }  }    public void push(Node n){   if(n != null){    n.next = top;    top = n;   }  } }

队列（Queue）

class Queue{  Node first, last;  public void enqueue(Node n){   if(first == null){    first = n;    last = first;   }else{    last.next = n;    last = n;   }  }  public Node dequeue(){   if(first == null){    return null;   }else{    Node temp = new Node(first.val);    first = first.next;    return temp;   }   } }

值得一提的是，Java标准库中已经包含一个叫做Stack的类，链表也可以作为一个队列使用（add()和remove()）。（链表实现队列接口）如果你在面试过程中，需要用到栈或队列解决问题时，你可以直接使用它们。

在实际中，需要用到链表的算法有：

插入两个数字
重新排序列表
链表周期
Copy List with Random Pointer
合并两个有序列表
合并多个排序列表
从排序列表中删除重复的
分区列表
LRU缓存

3.树&堆

这里的树通常是指二叉树。

class TreeNode{  int value;  TreeNode left;  TreeNode right; }

下面是一些与二叉树有关的概念：

二叉树搜索：对于所有节点，顺序是：left children <= current node <= right children；
平衡vs.非平衡：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树；
满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点；
完美二叉树（Perfect Binary Tree）：一个满二叉树，所有叶子都在同一个深度或同一级，并且每个父节点都有两个子节点；
完全二叉树：若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

堆（Heap）是一个基于树的数据结构，也可以称为优先队列（ PriorityQueue ），在队列中，调度程序反复提取队列中第一个作业并运行，因而实际情况中某些时间较短的任务将等待很长时间才能结束，或者某些不短小，但具有重要性的作业，同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。

下面列出一些基于二叉树和堆的算法：

二叉树前序遍历
二叉树中序遍历
二叉树后序遍历
字梯
验证二叉查找树
把二叉树变平放到链表里
二叉树路径和
从前序和后序构建二叉树
把有序数组转换为二叉查找树
把有序列表转为二叉查找树
最小深度二叉树
二叉树最大路径和
平衡二叉树

4.Graph

与Graph相关的问题主要集中在深度优先搜索和宽度优先搜索。深度优先搜索非常简单，你可以从根节点开始循环整个邻居节点。下面是一个非常简单的宽度优先搜索例子，核心是用队列去存储节点。

面试常见十大类算法汇总

第一步，定义一个GraphNode

class GraphNode{   int val;  GraphNode next;  GraphNode[] neighbors;  boolean visited;    GraphNode(int x) {   val = x;  }    GraphNode(int x, GraphNode[] n){   val = x;   neighbors = n;  }    public String toString(){   return "value: "+ this.val;   } }

第二步，定义一个队列

class Queue{  GraphNode first, last;    public void enqueue(GraphNode n){   if(first == null){    first = n;    last = first;   }else{    last.next = n;    last = n;   }  }    public GraphNode dequeue(){   if(first == null){    return null;   }else{    GraphNode temp = new GraphNode(first.val, first.neighbors);    first = first.next;    return temp;   }   } }

第三步，使用队列进行宽度优先搜索

public class GraphTest {    public static void main(String[] args) {   GraphNode n1 = new GraphNode(1);    GraphNode n2 = new GraphNode(2);    GraphNode n3 = new GraphNode(3);    GraphNode n4 = new GraphNode(4);    GraphNode n5 = new GraphNode(5);      n1.neighbors = new GraphNode[]{n2,n3,n5};   n2.neighbors = new GraphNode[]{n1,n4};   n3.neighbors = new GraphNode[]{n1,n4,n5};   n4.neighbors = new GraphNode[]{n2,n3,n5};   n5.neighbors = new GraphNode[]{n1,n3,n4};     breathFirstSearch(n1, 5);  }    public static void breathFirstSearch(GraphNode root, int x){   if(root.val == x)    System.out.println("find in root");     Queue queue = new Queue();   root.visited = true;   queue.enqueue(root);     while(queue.first != null){    GraphNode c = (GraphNode) queue.dequeue();    for(GraphNode n: c.neighbors){       if(!n.visited){      System.out.print(n + " ");      n.visited = true;      if(n.val == x)       System.out.println("Find "+n);      queue.enqueue(n);     }    }   }  } }

输出结果：

value: 2 value: 3 value: 5 Find value: 5value: 4

实际中，基于Graph需要经常用到的算法：

克隆Graph

5.排序

不同排序算法的时间复杂度，大家可以到wiki上查看它们的基本思想。

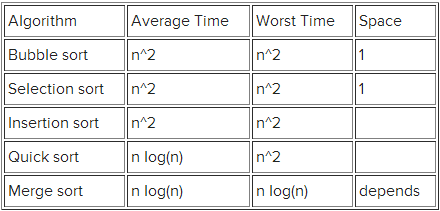
面试常见十大类算法汇总

BinSort、Radix Sort和CountSort使用了不同的假设，所有，它们不是一般的排序方法。

下面是这些算法的具体实例，另外，你还可以阅读： Java开发者在实际操作中是如何排序的。

归并排序
快速排序
插入排序

6.递归和迭代

下面通过一个例子来说明什么是递归。

问题：

这里有n个台阶，每次能爬1或2节，请问有多少种爬法？

步骤1：查找n和n-1之间的关系

为了获得n，这里有两种方法：一个是从第一节台阶到n-1或者从2到n-2。如果f(n)种爬法刚好是爬到n节，那么f(n)=f(n-1)+f(n-2)。

步骤2：确保开始条件是正确的

f(0) = 0;f(1) = 1;

public static int f(int n){  if(n <= 2) return n;  int x = f(n-1) + f(n-2);  return x; }

递归方法的时间复杂度指数为n，这里会有很多冗余计算。

f(5) f(4) + f(3) f(3) + f(2) + f(2) + f(1) f(2) + f(1) + f(2) + f(2) + f(1)

该递归可以很简单地转换为迭代。

public static int f(int n) {    if (n <= 2){   return n;  }    int first = 1, second = 2;  int third = 0;    for (int i = 3; i <= n; i++) {   third = first + second;   first = second;   second = third;  }    return third; }

在这个例子中，迭代花费的时间要少些。关于迭代和递归，你可以去这里看看。

7.动态规划

动态规划主要用来解决如下技术问题：

通过较小的子例来解决一个实例；
对于一个较小的实例，可能需要许多个解决方案；
把较小实例的解决方案存储在一个表中，一旦遇上，就很容易解决；
附加空间用来节省时间。

上面所列的爬台阶问题完全符合这四个属性，因此，可以使用动态规划来解决：

public static int[] A = new int[100];   public static int f3(int n) {  if (n <= 2)   A[n]= n;    if(A[n] > 0)   return A[n];  else   A[n] = f3(n-1) + f3(n-2);//store results so only calculate once!  return A[n]; }

一些基于动态规划的算法：

编辑距离
最长回文子串
单词分割
最大的子数组

8.位操作

位操作符：

面试常见十大类算法汇总

从一个给定的数n中找位i（i从0开始，然后向右开始）

public static boolean getBit(int num, int i){  int result = num & (1<<i);    if(result == 0){   return false;  }else{   return true;  } }

例如，获取10的第二位：

i=1, n=10 1<<1= 10 1010&10=10 10 is not 0, so return true;

典型的位算法：

Find Single Number
Maximum Binary Gap

9.概率

通常要解决概率相关问题，都需要很好地格式化问题，下面提供一个简单的例子：

有50个人在一个房间，那么有两个人是同一天生日的可能性有多大？（忽略闰年，即一年有365天）

算法：

public static double caculateProbability(int n){  double x = 1;     for(int i=0; i<n; i++){   x *=  (365.0-i)/365.0;  }    double pro = Math.round((1-x) * 100);  return pro/100; }

结果：

calculateProbability(50) = 0.97