MLlearning（1）——kNN算法
这篇文章讲kNN（k近邻， k -Nearest Neighbour）。这是一种lazy-learning，实现方便，很常用的分类方法。约定n为样本集中的样本数，m为样本的维度，则这个算法的训练复杂度为0，未加优化（线性扫描）的分类时间复杂度为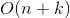 
，kd-Tree优化后复杂度可降为 
。
思路、优点及缺陷
该方法的思路是：如果一个样本在特征空间中的 k 个最相似即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。k NN 算法中，所选择的邻居都是已经正确分类的对象。该方法在分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
该方法在处理 多分类问题（multi-modal,对象具有多个类别标签）时，表现比SVM的要好，而且是最简单的分类方法，无需训练。
该方法对于样本的要求较高，不能给出数量不均衡的样本，否则会出现大容量的样本填充了选取的k个样本中的多个，而这些样本距离输入对象的特征距离其实是很远的。对于这种极端情况，在没办法获得更多样本情况下，可以通过加权的WAkNN (weighted adjusted k nearest neighbor)解决。另外，这种方法的时间复杂度较高，且kd-Tree会在维数高时（一般是当m>10时）遭遇维数灾难（Curse of Dimensionality），时间复杂度退化至线性扫描（由于常数问题，实际耗时会比线性扫描更高）。
Lua实现
为了方便起见，通常把特征空间看做一个欧式空间。两个向量之间的距离可由欧氏距离公式直接得出： 
有了这个假设，就可以直接把特征作为向量处理，进行kNN的计算。
这里笔者用Lua简单实现了朴素的kNN算法，源码托管于github，其中还包括手写数字识别的Demo： https://github.com/Darksun2010/MLlearning/tree/master/kNN
实验——测试算法速度及正确率
在git上clone代码后，载入其中识别数字的Demo。调用其中函数 testkNN() ，会测试此Demo，返回两个值：样本总数及错误率。
笔者电脑上的结果如下(k=3)：
>print(testkNN())
answer of kNN: 0 , correct answer: 0
...
answer of kNN: 9 , correct answer: 9
946 0.011627906976744
错误率仅为约1.2%，相当不错的成绩！经试验，k=3对于这个样本集是最好的选择。另外，我选择用Lua语言实现它的原因有三：
- 我喜欢Lua
- Lua嵌入性强
- LuaJIT的执行效率比Python/CPython高好几个数量级，直逼C/C++的执行效率！
后记
kNN只是个开始，我会写更多的文字，介绍更多的机器学习算法。
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
