【十大经典数据挖掘算法】k-means
1. 引言
k-means与kNN虽然都是以k打头,但却是两类算法——kNN为监督学习中的分类算法,而k-means则是非监督学习中的聚类算法;二者相同之处:均利用近邻信息来标注类别。
聚类是数据挖掘中一种非常重要的学习流派,指将未标注的样本数据中相似的分为同一类,所谓“物以类聚,人以群分”嘛。k-means是聚类算法中最为简单、高校的,核心思想:由用户指定k个初始质心(initial centroids),以作为聚类的类别(cluster),重复迭代直至算法收敛。
2. 基本算法
在k-means算法中,用质心来表示cluster;且容易证明k-means算法收敛等同于所有质心不再发生变化。基本的k-means算法流程如下:
选取k个初始质心(作为初始cluster); repeat: 对每个样本点,计算得到距其最近的质心,将其类别标为该质心所对应的cluster; 重新计算k个cluser对应的质心; until 质心不在发生变化对于欧式空间的样本数据,以平方误差和(sum of the squared error, SSE)作为聚类的目标函数,同时也可以衡量不同聚类结果好坏的指标:
/[ SSE=/sum/limits_{i=1}^{k} /sum_{x/in C_{i}} dist(x, c_i) /]
表示样本点 /(x/) 到cluster /(C_i/) 的质心 /(c_i/) 距离平方和;最优的聚类结果应使得SSE达到最小值。
下图中给出了一个通过4次迭代聚类3个cluster的例子:

k-means存在缺点:
-
k-means是局部最优的,容易受到初始质心的影响;比如在下图中,因选择初始质心不恰当而造成次优的聚类结果(SSE较大):
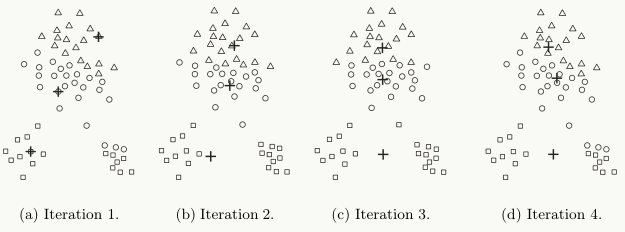
-
同时,k值的选取也会直接影响聚类结果,最优聚类的k值应与样本数据本身的结构信息相吻合,而这种结构信息是很难去掌握,因此选取最优k值是非常困难的。
3. 优化
为了解决上述存在缺点,在基本k-means的基础上发展了二分(bisecting) k-means,其主要思想:一个大cluster进行分裂后可以得到两个小的cluster;为了得到k个cluster,可进行k-1次分裂。算法流程如下:
初始时只有一个cluster包含所有样本点; repeat: 从待分裂的clusters中选择一个进行二元分裂,所选的cluster应使得SSE最小; until 有k个cluster上述算法流程中,为从待分裂的clusters中求得局部最优解,可以采取暴力方法:依次对每个待分裂的cluster进行二元分裂(bisect)以求得最优分裂。二分k-means算法聚类过程如图:
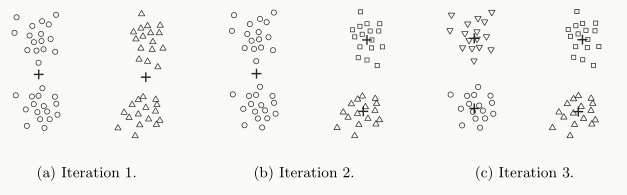
从图中,我们容易观察到:二分k-means算法对初始质心的选择不太敏感,因为初始时只选择一个质心。











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

