转载

BABY夜谈大数据：计算文本相似度

简单讲解

上一章有提到过[基于关键词的空间向量模型]的算法，将用户的喜好以文档描述并转换成向量模型，对商品也是这么处理，然后再通过计算商品文档和用户偏好文档的余弦相似度。

文本相似度计算在信息检索、数据挖掘、机器翻译、文档复制检测等领域有着广泛的应用。

比如舆论控制，我们假设你开发了一个微博网站，并且已经把世界上骂人的句子都已经收录进了数据库，那么当一个用户发微博时会先跟骂人句子的数据库进行比较，如果符合里面的句子就不让用户发出。

通常情况下，很多工程师就会想到用like或者where的sql语法去查找。可是当情况更为复杂呢？

数据库存放了“你是个坏人”，用户要发“小明是个坏人”，这时应该怎么办呢？

最简单的办法就是通过判断文本的相似程度来决定用户发的内容是否是骂人的。

本章节就几种简单的判断文本相似性的算法来讲解，帮助大家更好的理解。

相关算法

1、余弦相似性

余弦（余弦函数），三角函数的一种。在Rt△ABC（直角三角形）中，∠C=90°，角A的余弦是它的邻边比三角形的斜边，即cosA=b/c，也可写为cosA=AC/AB。余弦函数：f（x）=cosx（x∈R）

BABY夜谈大数据：计算文本相似度

这是一个非常常见的算法，相信大家都应该学过余弦定理了，简单来说这个算法就是通过计算两个向量的夹角余弦值来评估他们的相似度。

对于二维空间，根据向量点积公式，显然可以得知（ps，这个公式不是这个算法的重点，可以不用强记）：

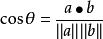
BABY夜谈大数据：计算文本相似度

假设向量a、b的坐标分别为(x1,y1)、(x2,y2) 。则：

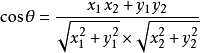
BABY夜谈大数据：计算文本相似度

设向量 A = (A1,A2,...,An)，B = (B1,B2,...,Bn) 。推广到多维，数学家已经帮我们证明了，所以你只要记住下面的公式：

BABY夜谈大数据：计算文本相似度

简单来说可以写成下面的式子：

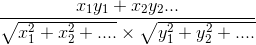
BABY夜谈大数据：计算文本相似度

（式子中的x和y是指词频）

比如我们要判断两句话

A=你是个坏人 B=小明是个坏人

① 先进行分词

A=你 / 是 / 个 / 坏人 B=小明 / 是 / 个 / 坏人

② 列出所有的词

{ 你小明是个坏人 }

③计算词频（出现次数）

A={1 0 1 1} (每个数字对应上面的字) B={0 1 1 1}

然后把词频带入公式

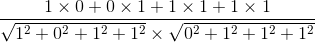
BABY夜谈大数据：计算文本相似度

最终=0.667(只余3位)，可以百度"2除以(根号3乘以根号3)"看到计算结果。

余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"。

简单来说上面计算出的值代表两个句子大概六成相似，越接近1就越相似。

2、简单共有词

通过计算两篇文档共有的词的总字符数除以最长文档字符数来评估他们的相似度。

假设有A、B两句话，先取出这两句话的共同都有的词的字数然后看哪句话更长就除以哪句话的字数。

同样是A、B两句话，共有词的字符长度为4，最长句子长度为6，那么4/6，≈0.667。

3、编辑距离

编辑距离（Edit Distance），又称Levenshtein距离，是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。一般来说，编辑距离越小，两个串的相似度越大。由俄罗斯科学家Vladimir Levenshtein（找不到他照片233333）在1965年提出这个概念。

例如将“BABAY是个好人”转成“BABY是个帅哥”，编辑举例就是2~~（好人变帅哥只要2就好...）~~： BABY是个帅人（好→帅） BABY是个帅哥（人→哥）

然后拿编辑距离去除以两者之间的最大长度，2/6≈0.333，意味着只要变动这么多就可以从A变成B，所以不用变动的字符便代表了相似度，1-0.333＝0.667。

4、SimHash + 汉明距离

simhash是谷歌发明的算法，据说很nb，可以将一个文档转换成64位的字节，然后我们可以通过判断两个字节的汉明距离就知道是否相似了。

汉明距离是以理查德·卫斯里·汉明的名字命名的。在信息论中，两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。例如：

1011101 与 1001001 之间的汉明距离是 2。

"toned" 与 "roses" 之间的汉明距离是 3。

首先我们来计算SimHash：

① 提取文档关键词得到[word,weight]这个一个数组。（举例 [美国，4]）

② 用hash算法将word转为固定长度的二进制值的字符串[hash(word),weight]。（举例 [100101，4]）

③ word的hash从左到右与权重相乘，如果为1则乘以1 ，如果是0则曾以-1。（举例4,-4,-4,4,-4,4）

④ 接着计算下个数，直到将所有分词得出的词计算完，然后将每个词第三步得出的数组中的每一个值相加。（举例美国和51区，[4,-4,-4,4,-4,4]和[5 -5 5 -5 5 5]得到[9 -9 1 -1 1 9]）