【函数式】Monads模式初探——Functor
函子与范畴
函子(functor)是 从一个范畴到另一个范畴的转换 ,并且其亦可转换/保持态射(morphism)。
一个 态射 是从一个范畴里的一个值到同一个范畴里的另一个值的变换。在猫的范畴的例子里,一个态射好比一个盒子,能够把黯淡无光的猫转化为一个霓虹闪耀的猫。在类型的范畴里(计算机科学常用的范畴),一个态射是一个把某类型转化为另一个类型的函数。
函子是可以把猫转化为狗的东西(不同范畴的转换)。函子可以把暗淡的猫转换成暗淡的狗,光彩的猫转换成光彩的狗。函子还可以连态射都转换过去,这样可以把暗淡的狗转化为光彩的狗。
 图中,下面的圈子表示所有的类型组成的范畴。里面包括标准的String、Double和其他Scala能定义的类型。函子F是Scala里的一个类型构造器。对于一个范畴中的任意类型T,可以把该类型置于类型构造器
图中,下面的圈子表示所有的类型组成的范畴。里面包括标准的String、Double和其他Scala能定义的类型。函子F是Scala里的一个类型构造器。对于一个范畴中的任意类型T,可以把该类型置于类型构造器 F[_] 中,从而得到一个新类型 F[T] 。
对函子的描述
函子本质上是范畴之间的转换。

上图表示范畴C到范畴D的函子。图中,对象A和B被转换到了范畴D中同一个对象,因此,态射g就被转换成了一个源对象和目标对象相同的态射(不一定是单位态射),而且id_A和id_B变成了相同的态射。对象之间的转换是用浅黄色的虚线箭头表示,态射之间的转换是用蓝紫色的箭头表示。
范畴之间的转换必须在转换时保留所有的态射才能称为函子转换。也就是说,如果在第一个范畴有个操作类型的函数,那么我们也应该有个转换后的函数能够操作转换后的类型。比如说,如果我们有个吧String转换为Int的函数,那么我们也应该能够把F[String]转换成F[Int],这正是map方法所提供的功能。
trait Functor[F[_]] { defapply[A](x: A):F[A] defmap[A,B](x: F[A])(f: A => B):F[B] } apply方法的作用——对于任意类型A,一个函子能够在新范畴里构造一个类型F[A]。map方法的作用——给定一个转换后的类型F[A]和一个在原范畴里的态射A => B,能够创建一个F[B]类型的结果。也就是说,我们有个新函数能够接受F[A],返回F[B]。
简单的说,函子是实现了map方法的数据类型。举例来说,
trait Functor[F[_]] { deffmap[A,B](x: F[A])(f: A => B):F[B] } object ListFunctor extends Functor[List] { deffmap[A,B](list: List[A])(f: A => B):List[B] = list map f } val l1 = List(1,2,3) val result = ListFunctor.fmap(l1)(i => i+1) println(result) // printis // List(2,3,4) 函子的形象演示
假设有一个容器(container),这里的容器可以认为是一种上下文(context)或者是为函数提供的计算上下文(computational context)。
在图中表示为一个盒子。当一个元素被上下文包裹,我们不能简单的对该元素应用一般的运算方法,于是需要使用map函数(Haskell中称为fmap)。

map函数知道如何将普通函数应用到一个被上下文包裹的元素上。
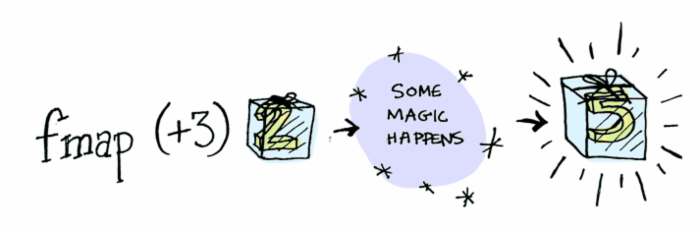
函子(functor)是定义了如何应用map的类型类(typeclass)。
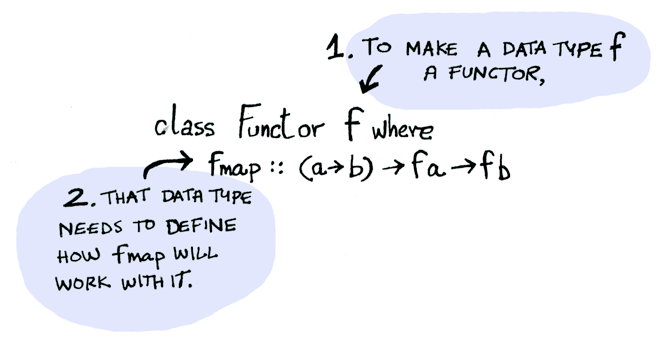
如果我们要将普通函数应用到一个有盒子上下文包裹的值,那么我们首先需要定义一个叫Functor的数据类型,在这个数据类型中需要定义如何使用map或fmap来应用这个普通函数。
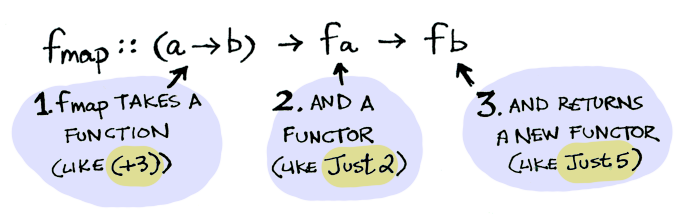
函子内部工作原理可以认为是这样的:
- 将值从上下文盒子中解救出来
- 将外部指定的函数(+3)应用到这个值上,得到一个新的值(5)
- 再将这个新值放入到上下文盒子中
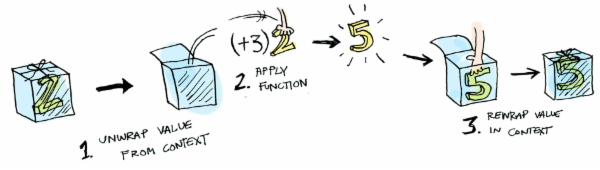
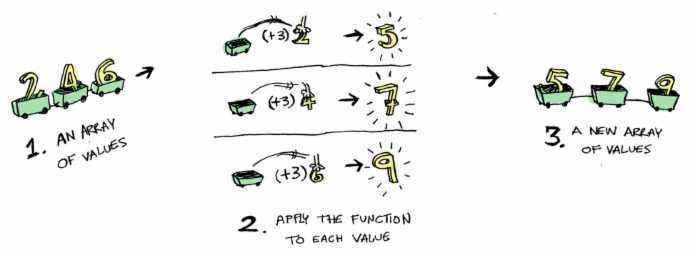
下图显示了如何将一个普通函数应用到值集合,不是单个值,而是值的集合数组中,图中数组函子将数组一个个打开(遍历),然后分别将普通函数应用到这些元素中,最后返回一个新的集合值。
补充:高阶类型
基本泛型:
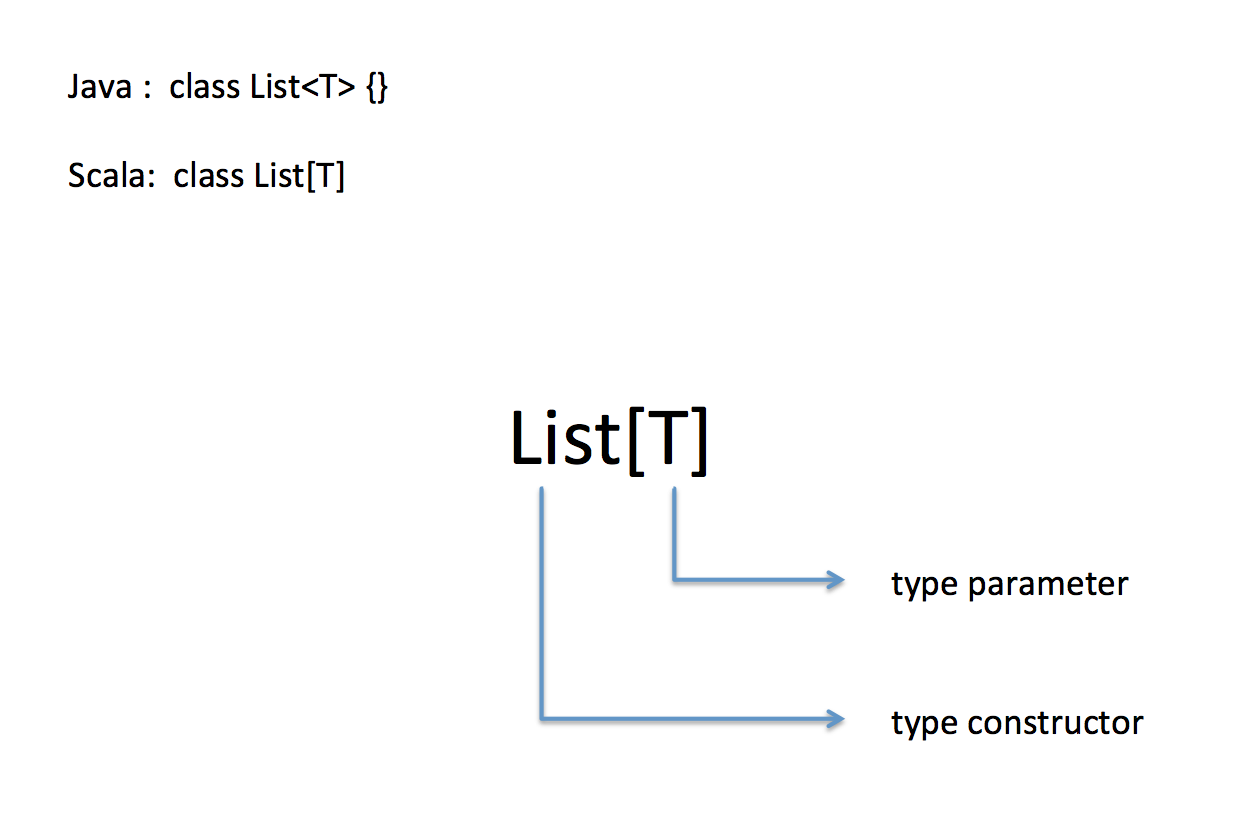
如果类型参数也是一个泛型(类型构造器):
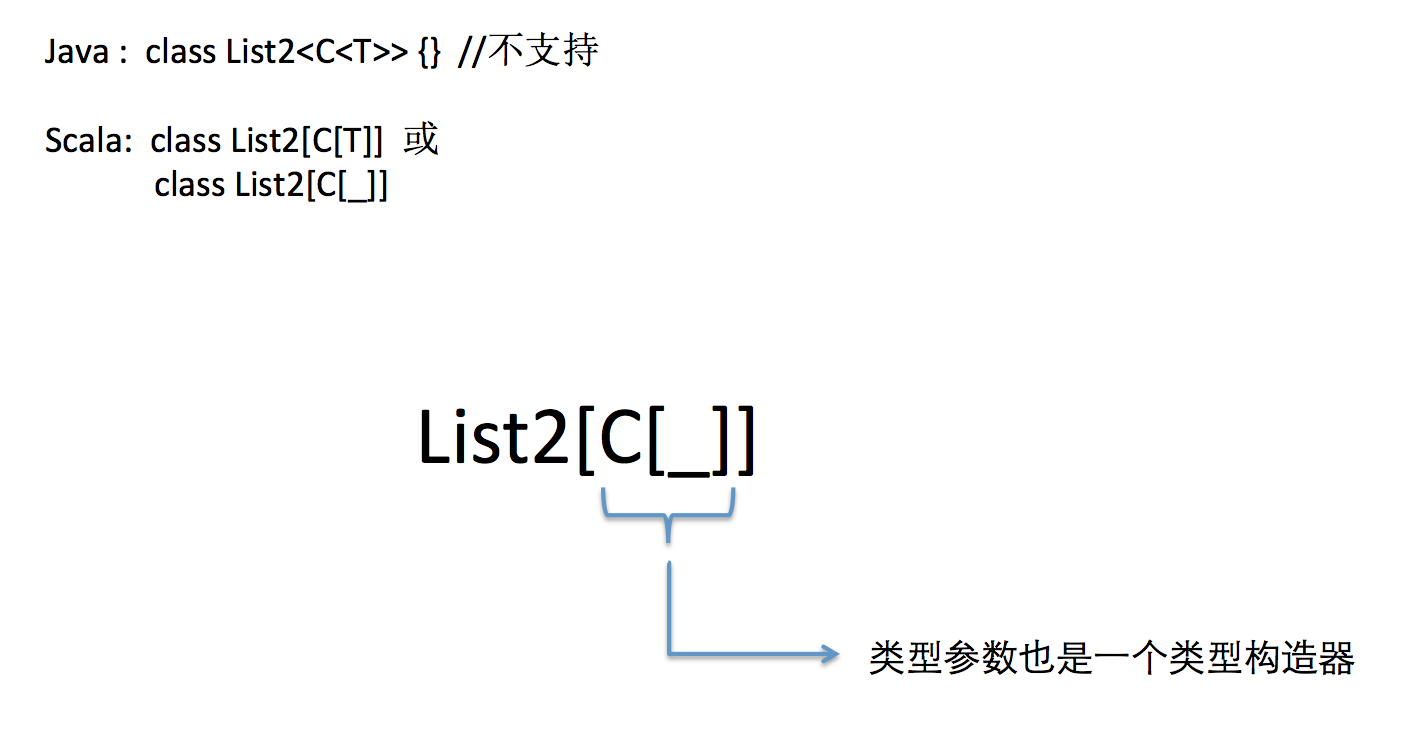
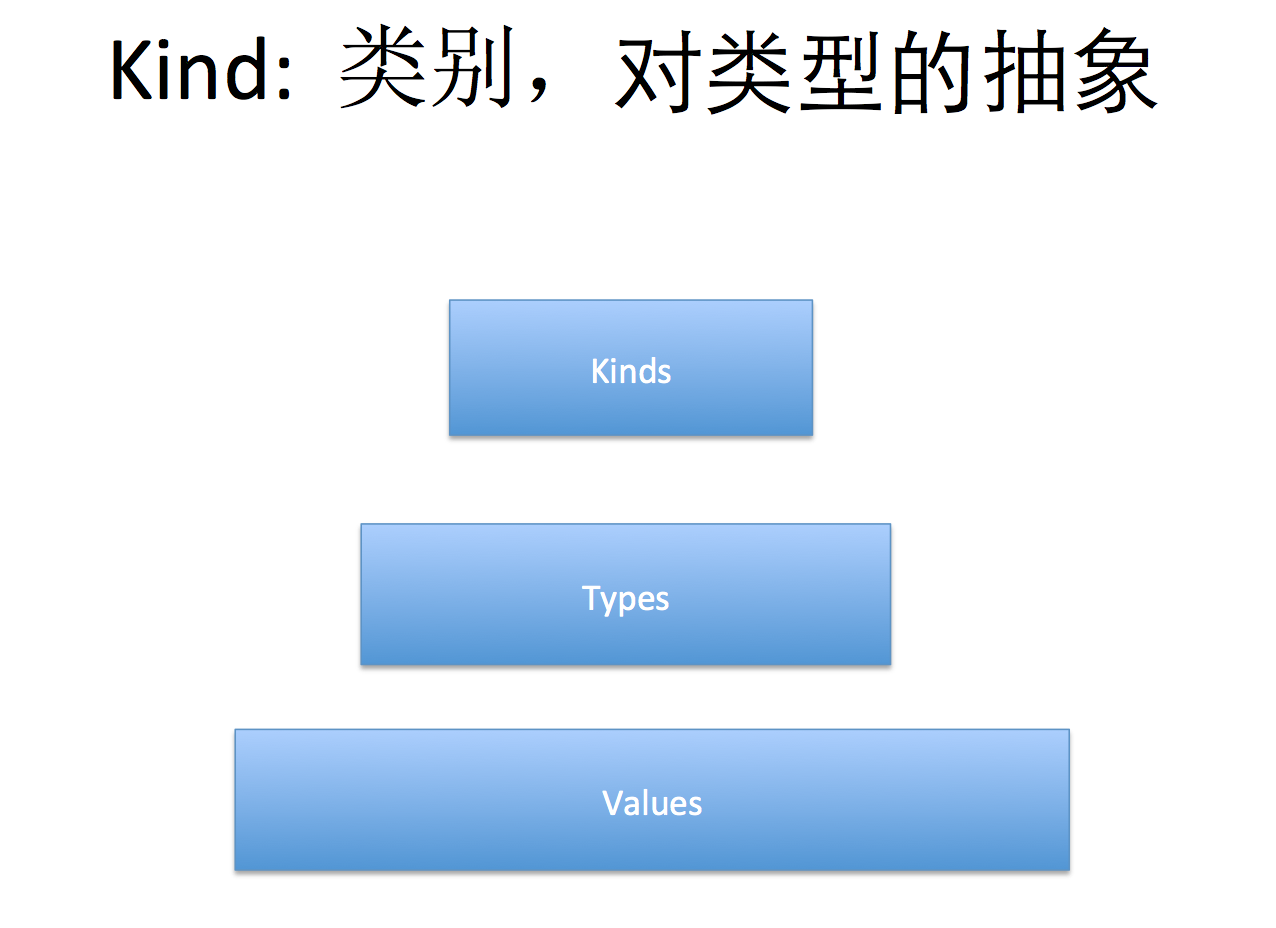
对类型的归纳:

类型(type)是对数据的抽象,而高阶类型(higher-kinded type)是对类型的抽象:
参考资料
函数编程中functor和monad的形象解释
深入理解Scala
理解高阶类型
Scala和范畴论 — 对Monad的一点认识转载请注明作者Jason Ding及其出处
jasonding.top
Github博客主页(http://blog.jasonding.top/)
CSDN博客(http://blog.csdn.net/jasonding1354)
简书主页(http://www.jianshu.com/users/2bd9b48f6ea8/latest_articles)
Google搜索jasonding1354进入我的博客主页










![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

