Union-Find
前言
开始刷 Coursera 的 Algorithms 课，在此尽量为每个 Lectures 写篇笔记。
Union-Find
并查集，顾名思义，主要两个操作。
-
union合并两个集合 -
find查询两个对象是否属于一个集合
一个集合称为 Connected components .
quick-find
用数组来保存数据。若两个数据的索引在数组中的值一样，则称两个数据在一个集合。
-
union(p,q)也就是data[p]=data[q],但是注意，所有和p在同一个集合的数都要链接到q集合。所以这里需要一个循环操作。 -
find(p,q)判断data[p]==data[q]
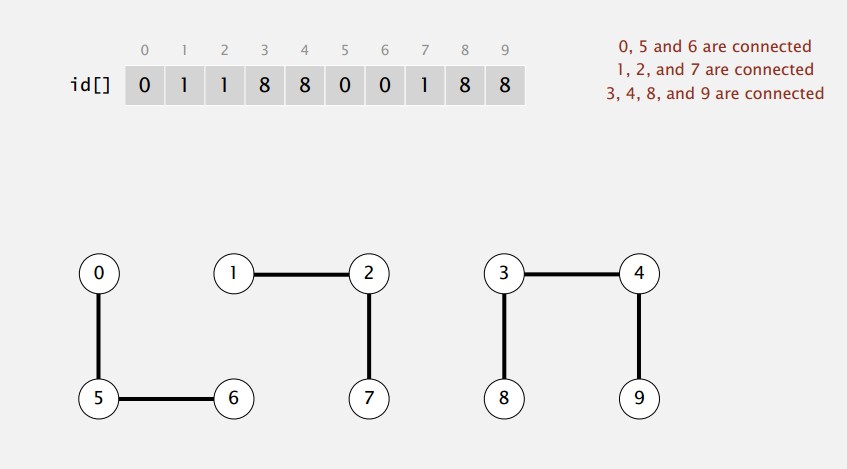
主要代码如下。
public class QF {
private int data[];
public QF(){
init();
}
private void init() {
data = new int[10];
for(int i=0;i<10;i++){
data[i]=i;
}
}
public boolean find(int p,int q){
return data[p]==data[q];
}
public void union(int p,int q){
int tp = data[p];
for(int i=0;i<data.length;i++){
if(data[i]==tp)
data[i]=data[q];
}
}
}
此方法查询效率很高。但是合并效率低。如果要合并n个集合，集合总共有m个数据，时间复杂度就是n的平方了，
quick-union
此方法改变存储方式，每个数字里的对象，以一颗树的方式来存储。每次合并的时候只要改变根节点即可。
主要储存方式为，比如说 index=1 的节点的父亲节点为 data[1] , index=1 的祖父节点为 data[data[1]] ，以此类推，如果 data[i]==i ,则找到了根节点。
-
union(p,q)改变p的根节点数组数据为q的根节点。data[root(p)]=root(q) -
find(p,q)判断p q的根节点是否相同。
private int root(int r){
while(data[r]!=r)
r=data[r];
return r;
}
public boolean find(int p,int q){
return root(p)==root(q);
}
public void union(int p,int q){
int rq=root(q);
int rp=root(p);
data[rq]=rp;
}
这个算法比刚才的效率高了不少，唯一要担心的是 root() 方法，此方法会遍历整棵树查找根节点，如果树太高的话。效率会受到一定影响，下面我进行一些优化。
改进quick-union
一个比较简单的方法是，每次在挂接树的时候。把节点较少的树挂到节点较多的树上，此方法能有效降低树的高度。
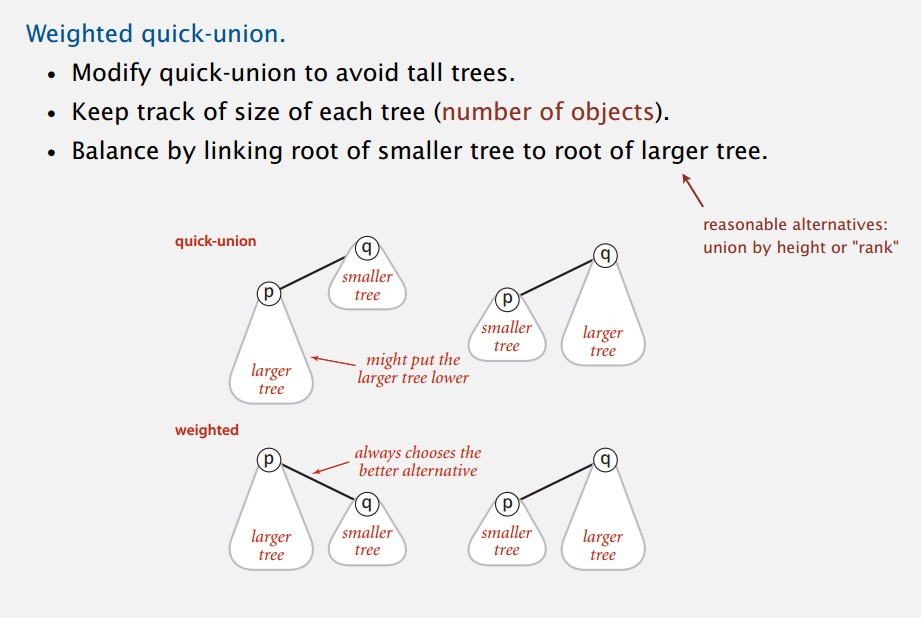
代码也很简单.
public void union(int p,int q){
int rq=root(q);
int rp=root(p);
if(size[rp]>=size[rq]){
data[rq]=rp;
size[rp]+=size[rq];
}
else{
data[rp]=rq;
size[rq]+=size[rp];
}
}
此时复杂度为 logN
path compression
另一种方法路径压缩。因为我们在使用并查集的时候并不关心数据顺序。所以可以在查询根节点时候，顺便压缩树的高度。
具体措施就是 把 index=1 的父节点 data[index] 挂接到他的祖父节点上也就是 data[data[index]]
一行代码，就搞定。时间复杂度也为 logN
private int root(int r){
while(data[r]!=r){
data[r]=data[data[r]]
r=data[r];
}
return r;
}
效率比较
Reference
Algorithms
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
