转载

相似文档 Shingling, Minhashing, Locality-sensitive hashing

本节关心的问题：找出内容近似的文档。

三个主要技术：

Shingling（N-gram）
Minhashing
Locality-sensitive hashing

流程：

文档->[Shingling]->k- shingles 集合(Boolean Matrix)->[Minhashing]->signature矩阵->[LSH]->候补的近似文档对

1 Shingling

文档中的k-shingle是文档中k个连续的字符：

Python

def shingles(text,k):  S = dict()  for i in range(len(text)-k+1):   if text[i:i+k] not in S:    S[text[i:i+k]] = 1   else:    S[text[i:i+k]] += 1  return S text = 'The dog which chased the cat' text2 = 'The dog that chased the cat' print shingles(text, 3).keys() ['sed', 'og ', 'cha', ' ch', 'ich', 'h c', ' ca', 'has', 'ch ', 'ed ', 'e d', 'g w', 'whi', 'e c', 'd t', 'ase', ' th', 'The', ' do', 'dog', ' wh', 'cat', 'hic', 'he ', 'the']

若k较大，可考虑用token 的方式减小shingles。

Python

def shingles(text,k,tokenize = False,klen = 20):  S = dict()  for i in range(len(text)-k):   s = text[i:i+3]   if tokenize and k > klen:    s = hash(s)   if s not in S:    S[s] = 1   else:    S[s] += 1  return S print shingles(text,3, True, 2).keys() [-531589997, -254223587, 398874913, 1935036066, 2126309027, 1190409000, 1935036075, 1255409211, 398874976, -1886291902, -1818291638, 187508811, -873956403, -1818291635, 1473775443, -1585925418, 1952036183, -1759726630, 1936036192, 1528775661, 1955036270, 1247409235, 1259409268, 332310010]

将文档用shingles，或shingles的token表示后，可以用杰卡德相似系数（Jaccard similarity）来计算两个文档的相似程度：

Python

def jaccardSimilarityOfTwoDict(D1,D2):  S1, S2 = set(D1.keys()), set(D2.keys())  return float(len(set.intersection(S1,S2)))/len(set.union(S1,S2)) S1 = shingles(text,3) S2 = shingles(text2,3) print jaccardSimilarityOfTwoDict(S1,S2) 0.548387096774

用boolean matrix来表示若干文档及其相应的shingles，矩阵每一列对应于一篇文档，每一列对应一个shingles，相似文档 Shingling, Minhashing, Locality-sensitive hashing

表示文档

中包含第

相似文档 Shingling, Minhashing, Locality-sensitive hashing

个shingles。

假设总共有6个shingles，文档1有第2,3,5个shingles，文档2有第1,3,5,6个shingles，求对应的布尔矩阵：

def generateBMatrix(Dicts, rowNames = None):     if rowNames == None:    rowNames = list(set(sum([d.keys() for d in Dicts])))     nrow, ncol = len(rowNames), len(Dicts)     M = np.zeros((nrow,ncol))     for i in range(nrow):    for j in range(ncol):   if rowNames[i] in Dicts[j].keys():       M[i][j] = 1     return M D1 = {1:1,  2:1,  4:1} D2 = {0:1,  2:1,  4:1,  5:1} Dicts = [D1,D2] M = generateBMatrix(Dicts, range(6)) print M [[ 0.  1.]  [ 1.  0.]  [ 1.  1.]  [ 0.  0.]  [ 1.  1.]  [ 0.  1.]]

矩阵中两列的相似度即为两篇文档的杰卡德相似系数。

Python

def jaccardSimilarityFromTwoArray(A1,A2):  return float(sum(A1+A2 == 2))/sum(A1+A2 != 0) def jaccardSimilarityFromBMatrix(M):  n = shape(M)[1]  retList = []  for i in range(n):   for j in range(i+1,n):    retList.append((i,j,jaccardSimilarityFromTwoArray(M[:,i],M[:,j])))  return retList print jaccardSimilarityFromBMatrix(M) [(0, 1, 0.4)]

即两篇文档的杰卡德相似系数为0.4

2 Minhashing

Minhashing的作用是从boolean矩阵生成signature矩阵。

假设将boolean矩阵里的行重新随机排列一下，对每一列相似文档 Shingling, Minhashing, Locality-sensitive hashing

而言， minhash 函数相似文档 Shingling, Minhashing, Locality-sensitive hashing

的作用是在重新排列的boolean矩阵里，第相似文档 Shingling, Minhashing, Locality-sensitive hashing

列中在从上往下数第几行里出现元素

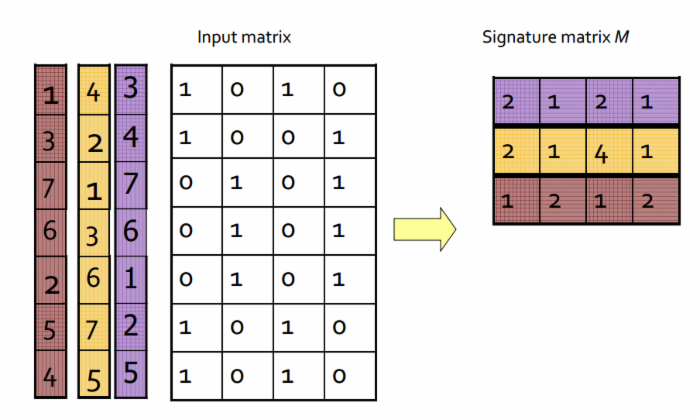
相似文档 Shingling, Minhashing, Locality-sensitive hashing

。

考虑如下boolean矩阵，左边彩色的格子表示的是三种对矩阵不同的随机排列，紫色的1对应于原布尔矩阵的第5行，表示按照紫色的排列重新排列后，原本矩阵的第5行被调换为新矩阵的第1行。右边的signature矩阵中，紫色的一行表示按照紫色的排列顺序重新排列的矩阵中，各列中首次出现相似文档 Shingling, Minhashing, Locality-sensitive hashing

的行数。

相似文档 Shingling, Minhashing, Locality-sensitive hashing

Python

BM  = np.matrix('1 0 1 0;1 0 0 1;0 1 0 1; 0 1 0 1; 0 1 0 1;1 0 1 0;1 0 1 0') print BM [[0 1 1 0]  [1 0 1 1]  [0 1 0 1]  [0 0 1 0]  [1 0 1 0]  [0 1 0 0]] def minhashing(BM, permu):  retList = np.array([0 for dummy in range(shape(BM)[1])])  for i in range(len(permu)):   if len(retList.nonzero()[0]) == len(retList):    return retList    break   else:    tup = BM[permu.index(i),:].getA()[0].nonzero()[0]    if len(tup) != 0:     for j in tup:      if retList[j] == 0:       retList[j] = i+1  return retList permu = [[2,3,6,5,0,1,4],    [3,1,0,2,5,6,4],    [0,2,6,5,1,4,3]] for p in permu:  print minhashing(BM, p) [2 1 2 1] [2 1 4 1] [1 2 1 2]

一个重要的属性：进行多次的重新排列和minhashing，两列相似文档 Shingling, Minhashing, Locality-sensitive hashing

出现

相似文档 Shingling, Minhashing, Locality-sensitive hashing

的概率等于两列的杰卡德相似系数。上面代码中是指定了重新排列的顺序，下面改为随机生成。

因此，不再需要比较两个布尔矩阵两列的相似度，可以根据signature矩阵中列的相似度来近似获对应文档的相似度。

Python

def signatureMatrix(BM,minhashNum = 100):  from random import shuffle  retMatrix = np.zeros((minhashNum,shape(BM)[1]))  permu = range(shape(BM)[0])  for i in range(minhashNum):   shuffle(permu)   retMatrix[i,:] = minhashing(BM, permu)  return retMatrix random.seed(123) sigM = signatureMatrix(BM) print sigM[1:5] [[ 1. 2. 4. 1.]  [ 1. 4. 1. 2.]  [ 1. 3. 1. 2.]  [ 1. 2. 1. 2.]] def similarityOfSignatures(sigM):  retList = []  n = shape(sigM)[1]  for i in range(n):   for j in range(i+1,n):    retList.append((i+1,j+1, /    float(sum(sigM[:,i]==sigM[:,j]))/shape(sigM)[0]))  return retList print similarityOfSignatures(sigM) [(1, 2, 0.0), (1, 3, 0.78), (1, 4, 0.13), (2, 3, 0.0), (2, 4, 0.74), (3, 4, 0.0)] print jaccardSimilarityFromBMatrix(BM) [(0, 1, 0.0), (0, 2, 0.75), (0, 3, 0.14285714285714285), (1, 2, 0.0), (1, 3, 0.75), (2, 3, 0.0)]

根据signature矩阵的计算结果表示第1,3两列相似度为0.78，第2,4两列的相似度为0.74

如果从布尔矩阵计算，则1,3两列相似度为0.75，第2,4两列的相似度为0.75。

实践中，如果布尔矩阵行数非常大，那么，存储行的随机排列，以及从原矩阵中依据排列顺序选出一行一行会非常麻烦。因此做如下近似：

随机选若干哈希函数（例如100）个，初始化一个空的矩阵相似文档 Shingling, Minhashing, Locality-sensitive hashing

，行数等于哈希函数的数量，列数等于文档数（即等于布尔矩阵列数），做如下操作：

相似文档 Shingling, Minhashing, Locality-sensitive hashing

得到的矩阵相似文档 Shingling, Minhashing, Locality-sensitive hashing

是signature矩阵的一个近似。

例子：

相似文档 Shingling, Minhashing, Locality-sensitive hashing

BM = np.matrix('1 0;0 1;1 1;1 0;0 1') hashes = [lambda x: x%5,     lambda x: (2*x+1)%5] def QuickSig(BM,hashes):  retMatrix = infty*np.ones((len(hashes),shape(BM)[1]))  for i in range(shape(BM)[0]):   hs = []   for h in hashes:    hs.append(h(i+1))   for j in range(shape(BM)[1]):    if BM[i,j] == 1:     for k in range(len(hs)):      if hs[k] < retMatrix[k,j]:       retMatrix[k,j] = hs[k]   print retMatrix  return retMatrix QuickSig(BM, hashes) [[  1.  inf]  [  3.  inf]] [[ 1.  2.]  [ 3.  0.]] [[ 1.  2.]  [ 2.  0.]] [[ 1.  2.]  [ 2.  0.]] [[ 1.  0.]  [ 2.  0.]] Out[12312]:  array([[ 1.,  0.],     [ 2.,  0.]])

上例中还是指定了哈希函数，哈希函数也可以使用随机生成的哈希函数。

再次考虑这个例子，不重新排列行再用minhash，而是使用100个随机生成的哈希函数，获得近似的signature矩阵。

相似文档 Shingling, Minhashing, Locality-sensitive hashing ：

Python

_memomask = {} def hash_function(n):  import random  mask = _memomask.get(n)  if mask is None:   random.seed(n)   mask = _memomask[n] = random.getrandbits(32)  def myhash(x):   return hash(x) ^ mask  return myhash BM  = np.matrix('1 0 1 0;1 0 0 1;0 1 0 1; 0 1 0 1; 0 1 0 1;1 0 1 0;1 0 1 0') random.seed(123) hashes = [hash_function(n) for n in range(100)] QsigM = QuickSig(BM, hashes) print similarityOfSignatures(QsigM) [(1, 2, 0.0), (1, 3, 0.77), (1, 4, 0.1), (2, 3, 0.0), (2, 4, 0.79), (3, 4, 0.0)]

即，在近似signature矩阵中，文档对1,3，以及文档对2,4的相似度分别为0.77和0.79

3 Locality-Sensitive Hashing

例如上面获得的近似signature矩阵，仍然有100行，如果生成的signature矩阵，仍然行数庞大，比较各个文档对相似文档 Shingling, Minhashing, Locality-sensitive hashing

仍然是较大的工程。局部敏感哈希的目的是避免这样庞大的运算。

如果将signature矩阵分为若干( 相似文档 Shingling, Minhashing, Locality-sensitive hashing

)段，然后对每一段的相似文档 Shingling, Minhashing, Locality-sensitive hashing

的小矩阵，用一个哈希函数对各列进行哈希，那么在这一段小矩阵内近似的列会被哈希到一起。如此循环，对所有

相似文档 Shingling, Minhashing, Locality-sensitive hashing

段都进行同样的操作。

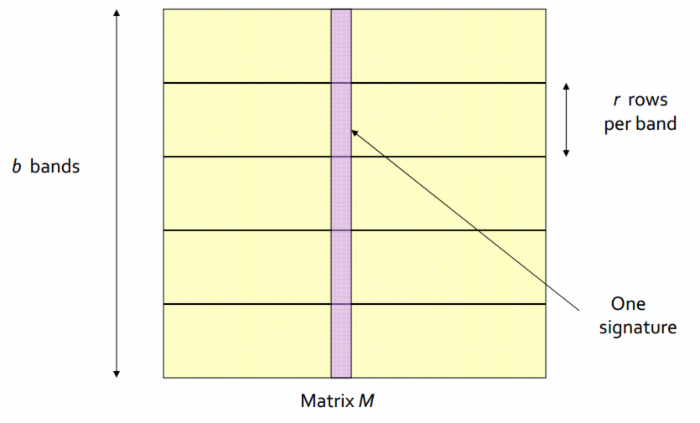
相似文档 Shingling, Minhashing, Locality-sensitive hashing

之后将至少在一段中被哈希到一起的列对，作为候选相似列对，输出出来。

Python

def LSH(SigMatrix, bands = math.ceil(float(shape(SigMatrix)[0])/2)):  blens = ceil(float(shape(SigMatrix)[0])/bands)  candidatePairs = {}  for b in range(int(bands)):   rows = SigMatrix[b*blens:min(shape(SigMatrix)[0],(b+1)*blens),:]   for i in range(shape(rows)[1]):    for j in range(i+1,shape(rows)[1]):     if sum(rows[:,i]==rows[:,j]) == len(rows[:,i]):      if (i,j) not in candidatePairs:       candidatePairs[(i,j)] = 1      else:       candidatePairs[(i,j)] += 1  return candidatePairs print LSH(sigM, 20) {(1, 3): 4, (0, 2): 5}

仍是上面的例子，通过20段的LSH获得的候补相似文档对为1,3和2,4。

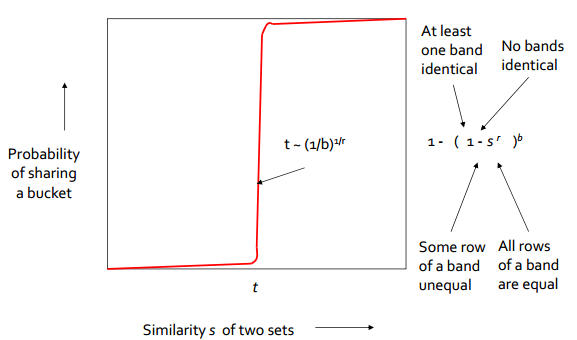
假设我们有100000篇文档，通过shingles和minhashing获得了一个相似文档 Shingling, Minhashing, Locality-sensitive hashing