转载

【译文】利用STAN做贝叶斯回归分析：Part 1 正态回归

作者 Lionel Hertzog

本文将介绍如何在R中做贝叶斯回归分析，你能在文末的参考文献中找到相关主题的更多信息。

贝叶斯回归

贝叶斯统计来自于贝叶斯公式，在回归分析中它一般被写作如下形式：

公式中【译文】利用STAN做贝叶斯回归分析：Part 1 正态回归是诸如斜率之类的待估参数集，是我们拥有的数据集。是参数的先验分布，也就是我们对于可取值的已有知识。是数据的似然函数（译者注：换一个角度就是样本的联合分布），【译文】利用STAN做贝叶斯回归分析：Part 1 正态回归就是对应的后验分布。这个等式包含了参数的先验信息（即“我”认为的回归系数的正负等等），又利用观测数据的似然函数将先验信息更新以得到后验分布。而所谓的后验分布，就是在给定观测数据和先验分布的情况下，相应参数的条件分布。在频率学派的框架下，似然函数是被研究的重点。但大多数时候我们并不关心给定参数时数据的出现概率，而是专注于诸如回归方程斜率为正的概率，参数 $【译文】利用STAN做贝叶斯回归分析：Part 1 正态回归$ 大于 $【译文】利用STAN做贝叶斯回归分析：Part 1 正态回归$ 的概率之类的问题。利用贝叶斯回归并计算其后验概率能直接回答这类问题。

在R中做贝叶斯回归

R中有不少包可以用来做贝叶斯回归分析，比如最早的（同时也是参考文献和例子最多的）R2WinBUGS包。这个包会调用WinBUGS软件来拟合模型，后来的JAGS软件也使用与之类似的算法来做贝叶斯分析。然而JAGS的自由度更大，扩展性也更好。近来，STAN和它对应的R包rstan一起进入了人们的视线。STAN使用的算法与WinBUGS和JAGS不同，它改用了一种更强大的算法使它能完成WinBUGS无法胜任的任务。同时STAN在计算上也更为快捷，能节约时间。

一个例子

让我们用仿真数据在STAN中进行回归分析。

首先我们需要写出一个模型表达式，如今网上有很多资源可以帮助你构造相应的模型。下面就以一个简单的正态回归模型为例：

/* *简单正态回归模型 */ data {     　int N; // 样本数量       　int N2; // new_X 矩阵大小       　int K; // 模型矩阵的列数       　real y[N]; // 响应变量y       　matrix[N, K] X; // 模型矩阵X      　 matrix[N2, K] new_X; // 预测值矩阵 } parameters {       vector[K] beta; // 回归模型中的参数       real sigma; // 标准差 } transformed parameters {       vector[N] linpred;       linpred <- X*beta; } model {         beta[1] ~ cauchy(0, 10); // 截距项的先验 （Gelman， 2008）        for(i in 2:K)        beta[i] ~ cauchy(0, 2.5); // 斜率项的先验 （Gelman， 2008）        y ~ normal(linpred, sigma); } generated quantities {       vector[N2] y_pred;       y_pred <- new_X*beta; // 模型预测的y的值 }

运行上述代码的最好方法是打开一个文本编辑器，复制它们并将其保存为.stan格式。

关于先验分布这里有些细节需要注意。先验分布的设定是贝叶斯分析中的一个重要话题，如果你对它有兴趣，可以参考《Probabilistic-Programming-and-Bayesian-Methods-for-Hackers》的第六章。此处我参考Gelman的文章（ Gelman， 2008 ）设定了弱信息先验（weakly informative priors）。我认为模型中大多数斜率项数值都很小，只有少部分值较大，因此先验分布选用了有着0均值和长尾的柯西分布。

接着让我们利用R完成后续工作，加载相应的包并生成一些仿真数据：

# 加载相应的包 library(rstan) library(coda) set.seed(20151204)  # 生成解释变量 dat <- data.frame(x1 = runif(100, -2, 2), x2 = runif(100, -2, 2))  # 设定模型 X <- model.matrix( ~ x1*x2, dat)  # 回归斜率项 betas <- runif(4, -1, 1)  # 仿真数据的标准差 sigma <- 1  # 生成y的仿真数据 y_norm <- rnorm(100, X%*%betas, sigma)  # 生成协变量的数据矩阵 new_X <- model.matrix( ~ x1*x2, expand.grid(x1 = seq(min(dat$x1), max(dat$x1), length = 20), x2 = c(min(dat$x2), mean(dat$x2), max(dat$x2))))

在这个例子中我生成了两个解释变量x1和x2，并仅在回归方程中放入了二者的交互项来解释y，数据在期望值附近呈正态分布。同时我也构造了一个new_X矩阵来拟合模型，它包括了由小到大排列的x1的值和x2的最小值，均值和最大值。由于x1与x2是以交互项的形式出现在模型里，我们就需要在x2的不同取值上拟合回归线。

接下来我们来对数据进行拟合：

# 设定文件保存路径 setwd("/home/lionel/Desktop/Blog/STAN/")  # 回归模型 m_norm <- stan(file = "normal_regression.stan", data = list(N = 100, N2 = 60, K = 4, y = y_norm, X = X, new_X = new_X), pars = c("beta", "sigma", "y_pred"))

stan函数会将模型文件和数据读入一个列表里，你在自己建模时要注意变量和模型文件的对应关系，函数中的pars参数用来指定要返回的参数。

STAN软件还在持续开发中，截至本文成稿，rstan的最新版本是2.8.2。在运行上述代码时，R的警告信息显示模型的尺度参数等于0，当然这并不值得担心。我接下来将会继续建模并绘制一些诊断图。

轨迹图和后验分布

# 画出参数的后验分布图 post_beta <- As.mcmc.list(m_norm, pars = "beta") plot(post_beta)

结果如下：

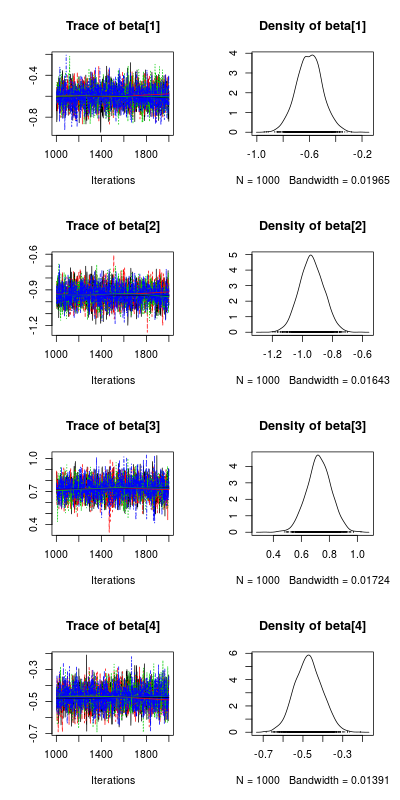
【译文】利用STAN做贝叶斯回归分析：Part 1 正态回归

左侧的图显示了各个参数的抽样轨迹，不同颜色代表了不同的马氏链。根据默认设置，每个参数一共有四条独立的马氏链，并且它们都收敛到了相似的值（因此右侧的概率分布都不是发散的）。右侧的图显示了四个参数的后验分布，它们为整个贝叶斯回归分析提供了最重要的信息。通过这些分布我们可以解决很多重要问题，比如：某个参数值大于0的概率是多少？

# 计算斜率项大于0的后验概率 apply(extract(m_norm, pars="beta")$beta, 2, function(x) length(which(x>0))/4000)  [1] 0 0 1 0

这个问题比较容易，参数beta[3]（y-norm对应x2的斜率）大于0的后验概率为1，其余参数大于0的后验概率为0.

两两相关性

另一个有用的总结性图表是参数间的相关图。如果某个参数能共提供独立的信息，那么它的散点图应该没有特定形状。如果某些参数间有比较强的相关性，那么它们可能不提供额外信息，你应该考虑删去一些参数。

# 绘制参数的相关图 pairs(m_norm, pars = "beta")

输出的图如下：

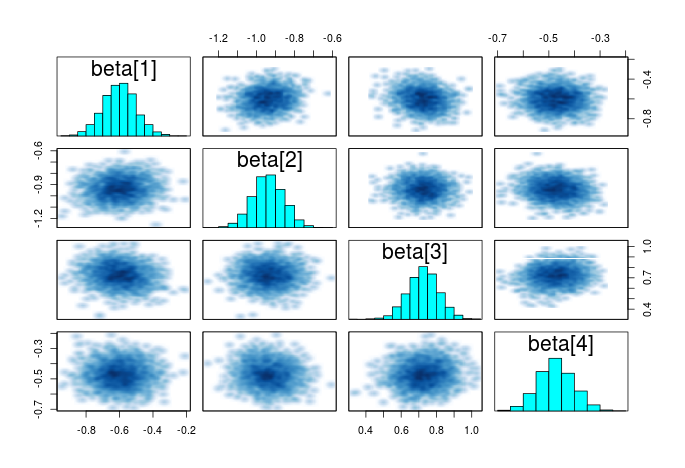
【译文】利用STAN做贝叶斯回归分析：Part 1 正态回归

参数的可信区间

可信区间是模型参数的另一类总结信息。下图中红色的可信带表示每个参数落入这个区间的概率是80%。与之相比，传统频率学派的置信区间则表示重复多次试验，参数值有80%的时间（试验次数）被包含于这个区间内。这无疑比较复杂难懂，其解释不如可信区间简单直观。

# 绘制不同beta值的可信区间 plot(m_norm, pars = c("beta", "sigma"))

输出结果如下：

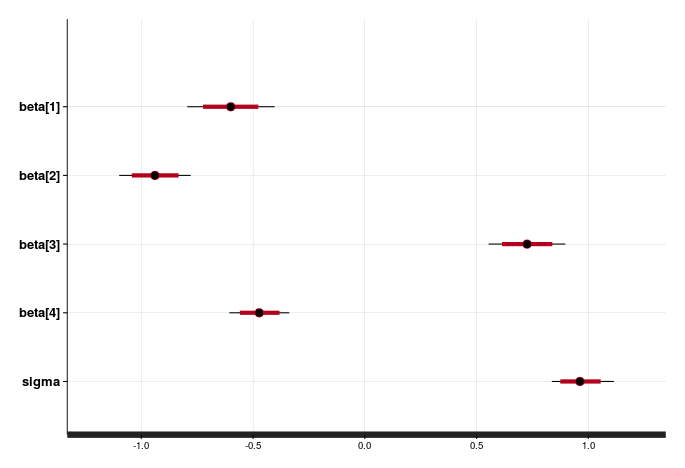
【译文】利用STAN做贝叶斯回归分析：Part 1 正态回归

回归线

最后，我们将在x2不同的取值上绘制相应的回归线和可信区间

绘制回归线和95%的可信带

new_x <- data.frame(x1 = new_X[, 2], x2 = rep(c("Min", "Mean", "Max"), each = 20)) new_y <- extract(m_norm, pars = "y_pred") pred <- apply(new_y[[1]], 2, quantile, probs = c(0.025, 0.5, 0.975)) # 参数中位数和95%可信带  # 画图 plot(dat$x1, y_norm, pch = 16) lines(new_x$x1[1:20], pred[2, 1:20], col = "red", lwd = 3) lines(new_x$x1[1:20], pred[2, 21:40], col = "orange", lwd = 3) lines(new_x$x1[1:20], pred[2, 41:60], col = "blue", lwd = 3) lines(new_x$x1[1:20], pred[1, 1:20], col = "red", lwd = 1, lty = 2) lines(new_x$x1[1:20], pred[1, 21:40], col = "orange", lwd = 1, lty = 2) lines(new_x$x1[1:20], pred[1, 41:60], col = "blue", lwd = 1, lty = 2) lines(new_x$x1[1:20], pred[3, 1:20], col = "red", lwd = 1, lty = 2) lines(new_x$x1[1:20], pred[3, 21:40], col = "orange", lwd = 1, lty = 2) lines(new_x$x1[1:20], pred[3, 41:60], col = "blue", lwd = 1, lty = 2) legend("topright",legend=c("Min","Mean","Max"), lty = 1, col = c("red", "orange", "blue"), bty = "n", title = "Effect of x2 value on/nthe regression")

输出的图如下：

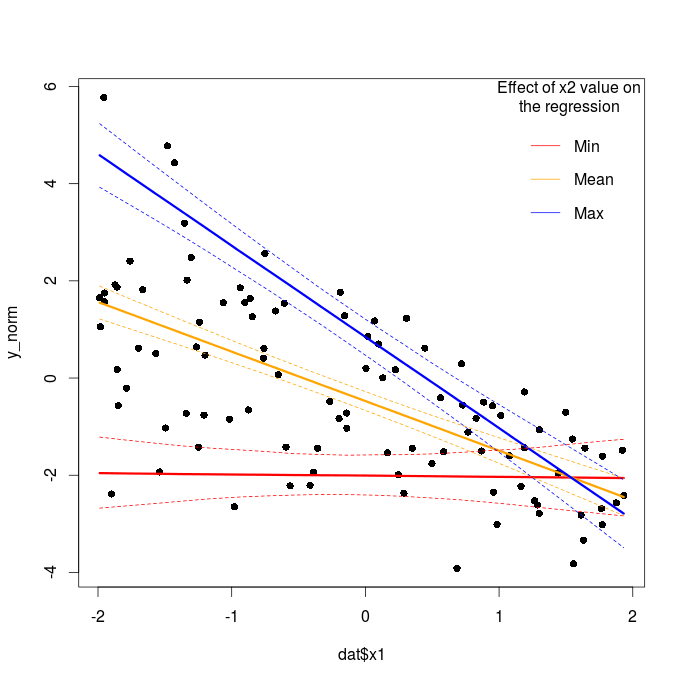
【译文】利用STAN做贝叶斯回归分析：Part 1 正态回归

通过过这个图我们可以发现在x2的值比较小的时候，不论x1取值如何y几乎是个常数。当x2的值逐渐变大，y与x1之间的负相关关系也越来越强（回归线变得陡峭）。

总结

本文展示了如何利用STAN软件拟合正态回归模型，并得到一系列重要的模型统计量。例子中所给出的模型形式非常的灵活，可以用来拟合不同当量的数据集，但要切记解释变量在拟合模型前应当先标准化。STAN可以拟合多类模型，用来实现上述模型只是小试牛刀。在随后的文章中我们会重点讲解利用各类连接函数转变为非正态的广义线性模型和多层模型。