机器学习笔记-模型评估与模型选择

评价一个机器学习模型的好坏需要特定的评估方法，并据此对模型进行选择，从而得到一个更好的模型。本文主要是关于模型评估与模型选择的笔记，以及利用 scikit-learn 对 Logistic 回归进行的结果进行交叉检验。

1. 训练误差，测试误差与泛化误差

学习器（模型）在训练集上表现出来的误差称为 训练误差（training error） 或 经验误差（empirical error） ，这种误差可以通过损失函数进行描述：

$$E_{training}(f) = /frac{1}{N}/sum_{i=1}^NL(y_i, f(x_i)$$

其中 $L(/cdot)$ 为损失函数，$f$ 为模型，$N$ 为训练样本容量。很多机器学习算法的训练过程就是试图最小化这一训练误差。但是最小化训练误差并不一定就是一个好的模型，它有可能只是将训练样本中所有的特征都非常好地挖掘出来进行学习，但这些训练样本的某些特征有可能是具有特异性的，并不能推广到所有样本中，这就会导致模型的**过拟合（overfitting）**。模型在新数据集合上表现出来的误差，称为**泛化误差（generalization error）**。通常会通过实验测试来对模型的泛化误差进行评估，这时需要引入一些新的测试数据对模型进行检验，在测试数据上表现出来的误差称为**测试误差（testing error）**。测试误差为：

$$e_{test} = /frac{1}{N'}/sum_{i=1}^N' I(y_i /neq f(x_i))$$

其中 $I(/cdot)$ 为指标函数（indicator function），当$/cdot$为真是返回$1$ ，否则返回 $0$；$N'$ 为测试样本容量，测试准确率（或称为精度（accuracy））：

$$acc_{test} = 1 - e_{test}$$

2. 过拟合与欠拟合

训练误差很小而泛化误差很大时称为过拟合，与之相对的是**欠拟合（underfitting）**。例如多项式拟合：

$$f_M(x, /omega) = /omega_0 + /omega_1x + /omega_2x^2+/dots+/omega_Mx^M = /sum_{j=0}^M/omega_jx^j$$

当选取 $M$ 个参数进行训练时，可能出现下列情况：

当 $M = 0$ 和 $M = 1$ 时，模型为直线，拟合效果很差，即欠拟合；当 $M = 9$ 时，模型曲线经过了每一个训练数据点，训练误差为 0，但是无法预测新的数据，因此泛化误差很大，即过拟合。

3. 测试误差的评估方法

1. 留出法（hold-out）
2. 交叉验证法（cross validation）
3. 自助法（bootstrapping）
4. 调参（parameter tuning）

3.1 留出法

将数据集 $D$ 划分为 $S, T$：

$$D = S /cap T, S /cup T = /emptyset$$

并采用**分层采样（stratified sampling）**，通常选用 $2/3 - 4/5$ 用于训练。

3.2 交叉验证法

将 $D$ 划分为 $k$ 个大小相似的互斥子集：

$$D = D_1 /cup D_2 /cup /dots /cup D_k, D_i /cap D_j = /emptyset (i /neq j)$$

每次用 $k-1$ 个子集作为训练集，剩下一个作为测试集，称为**k折交叉验证（k-fold cross validation）**。$k$ 通常取 10，并随机使用不同划分重复 $p$ 次，最终取 $p$ 次结果均值，例如“10次10折交叉验证”。

假设数据集 $D$ 容量为 $m$，若 $k = m$，则称为**留一法（Leave-One-Out, LOO）**。留一法苹果结果比较准确，但计算开销也相应较大。

3.3 自助法

以**自助采样法（bootstrap sampling）**为基础，从 $D$ 中有放回地随机抽取 $m$ 次，得到同样包含 $m$ 个样本的 $D'$，$D$ 中有一部分样本会在 $D'$ 中出现多次，而另一部分则未出现，$m$ 次重采样始终未被采到的概率是：

$$/lim_{m/rightarrow/infty}(1-/frac{1}{m})^m /rightarrow /frac{1}{e} /approx 0.368$$

即 $36.8/%$ 的样本未出现在 $D'$。以 $D'$ 作为训练集，$D - D'$ 作为测试集。自助法在数据集较小、难以划分训练/测试集时很有用。

4. 性能度量

除了精度（$acc_{test}$）和错误率（$e_{test}$），还需要反映任务需求的性能度量指标。

1. 查准率、查全率与 $F_1$
2. ROC & AUC
3. 代价矩阵

4.1 查准率、查全率与 $F_1$

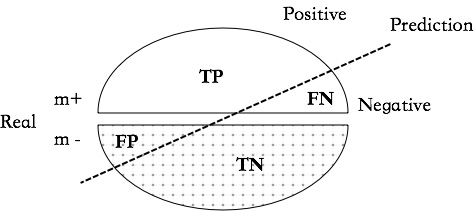
$$ TP + FP + TN + FN = m^++m^- = m$$

查准率（准确率，precision）： $$P = /frac{TP}{TP + FP}$$

查全率（召回率，recall）： $$R = /frac{TP}{TP + FN}$$

希望查全率高，意味着更看重决策的准确性，例如在商品推荐系统，尽量减少错误推荐；希望查全率高，意味着“宁可错杀一千”，例如在罪犯检测过程中。

$$F_1 = /frac{2PR}{P+R}$$ $$F_/beta = /frac{(1+/beta^2)PR}{(/beta^2+P)+R}$$

当 $/beta = 1$ 时，$F_/beta = F_1$；$/beta /gt 1$ 时，查全率影响更大；$/beta /lt 1$ 时，查准率影响更大。

4.2 信号检测论

$$TPR = /frac{TP}{TP + FN}$$ $$FPR = /frac{FP}{FP + TN}$$

在实验心理学信号检测论中，TPR 是**击中（Hit）**的概率，FPR 是 **虚惊（False alarm）**的概率。ROC（Receiver Operating Characteristic Curve）称为接受者操作特性曲线（又称感受性曲线）。曲线上各点反应相同的感受性，只是在不同的判定标准下所得的结果。以虚惊概率（FPR）为横轴，击中概率（TPR）为纵轴组成的坐标图和被试（学习模型）在相同刺激条件下采用不同判断标准得出不同结果画出的曲线。

曲线下区域的面积（Area Under ROC Curve, AUC）代表不同被试（模型）对刺激的辨别能力，AUC 越大，意味着辨别能力越强。

$$AUC = /frac{1}{2}/sum_{i=1}^{m-1}(x_{i+1}-x_i)(y_i+y_{i+1})$$

4.3 代价矩阵

暂略。

5. 统计检验

暂略。

6. 练习

《机器学习·周志华》习题 3.4：

选择： Adult Data Set

根据人口统计数据预测年收入是否超过 $50K（共14个属性，有不完整数据，暂时将不完整数据清除）。

head -n 5 adult.data  # 39, State-gov, 77516, Bachelors, 13, Never-married, Adm-clerical, Not-in-family, White, Male, 2174, 0, 40, United-States, <=50K # 50, Self-emp-not-inc, 83311, Bachelors, 13, Married-civ-spouse, Exec-managerial, Husband, White, Male, 0, 0, 13, United-States, <=50K # 38, Private, 215646, HS-grad, 9, Divorced, Handlers-cleaners, Not-in-family, White, Male, 0, 0, 40, United-States, <=50K # 53, Private, 234721, 11th, 7, Married-civ-spouse, Handlers-cleaners, Husband, Black, Male, 0, 0, 40, United-States, <=50K # 28, Private, 338409, Bachelors, 13, Married-civ-spouse, Prof-specialty, Wife, Black, Female, 0, 0, 40, Cuba, <=50K 

6.1 步骤

1. 利用 pandas 读取数据，将遗失数据（数据中以 ? 占位）剔除；
2. 将标字符串格式的标签转化为数字格式的类别（category）；
3. 分别用 KFold 和 LOO 的方法对对数回归模型进行验证。
4. 完整代码及计算过程见： Exe3.4

# 处理数据元信息 meta = """   age: continuous.   workclass: Private, Self-emp-not-inc, Self-emp-inc, Federal-gov, Local-gov, State-gov, Without-pay, Never-worked.   fnlwgt: continuous.   education: Bachelors, Some-college, 11th, HS-grad, Prof-school, Assoc-acdm, Assoc-voc, 9th, 7th-8th, 12th, Masters, 1st-4th, 10th, Doctorate, 5th-6th, Preschool.   education-num: continuous.   marital-status: Married-civ-spouse, Divorced, Never-married, Separated, Widowed, Married-spouse-absent, Married-AF-spouse.   occupation: Tech-support, Craft-repair, Other-service, Sales, Exec-managerial, Prof-specialty, Handlers-cleaners, Machine-op-inspct, Adm-clerical, Farming-fishing, Transport-moving, Priv-house-serv, Protective-serv, Armed-Forces.   relationship: Wife, Own-child, Husband, Not-in-family, Other-relative, Unmarried.   race: White, Asian-Pac-Islander, Amer-Indian-Eskimo, Other, Black.   sex: Female, Male.   capital-gain: continuous.   capital-loss: continuous.   hours-per-week: continuous.   native-country: United-States, Cambodia, England, Puerto-Rico, Canada, Germany, Outlying-US(Guam-USVI-etc), India, Japan, Greece, South, China, Cuba, Iran, Honduras, Philippines, Italy, Poland, Jamaica, Vietnam, Mexico, Portugal, Ireland, France, Dominican-Republic, Laos, Ecuador, Taiwan, Haiti, Columbia, Hungary, Guatemala, Nicaragua, Scotland, Thailand, Yugoslavia, El-Salvador, Trinadad&Tobago, Peru, Hong, Holand-Netherlands.   salary: <=50K, >50K   """ #?? 有没有更标准的方法可以把标签数据转化为数字？ names = []   catMap = {}   for line in meta.split("/n"):       line = line.strip()     if len(line) == 0:         continue     name, cate = tuple(line.split(":"))     names.append(name)     if 'continuous' in cate: # 数字类型的跳过         continue     catMap[name] = {v.strip(): i for i, v in enumerate(cate.rstrip(".").split(","))}  import numpy as np   import pandas as pd  # pandas 读取 csv 格式到 DataFrame datas = pd.read_csv('adult.data', header=None, names=names)   print(datas.shape)    # (32561, 15)  # 遗漏数据在文件中是 ?，替换成 NaN datas = datas.replace(r'/?', np.nan, regex=True)  # 剔除任何含有 NaN 的数据 datas = datas.dropna(how="any")   print(datas.shape)    # (30162, 15)  # 将 Object 类型转化成 category 并赋予整数值 for c in datas.columns:       if datas[c].dtype == 'object':         datas[c] = datas[c].apply(lambda x: catMap[c][x.strip()]) datas = datas.dropna(how="any")  # 分别将前 14 个属性和目标属性 salary 读入 X, y = datas[datas.columns[:-1]], datas.salary   X_arr = np.array(X)   y_arr = np.array(y)  # 10折交叉检验 from sklearn.cross_validation import KFold   kf = KFold(n=datas.shape[0], n_folds=10)   for train_index, test_index in kf:       X_train, X_test = X_arr[train_index], X_arr[test_index]     y_train, y_test = y_arr[train_index], y_arr[test_index]     print("---- Shapes: ", X_train.shape, X_test.shape) # ---- Shapes:  (27146, 14) (3016, 14)  X 10次  # 先取最后一折的数据进行测试： from sklearn.linear_model import LogisticRegression   from sklearn.preprocessing import StandardScaler  lr = LogisticRegression(penalty='l1', tol=0.01)   lr.fit(X_train, y_train)   lr.score(X_test, y_test)    # 0.83  # 或者直接用 cross_val_score from sklearn.cross_validation import cross_val_score   scores = cross_val_score(lr, X_arr, y_arr, cv=10)   print("Mean: ", np.mean(scores)) # 0.81  # 留一法 from sklearn.cross_validation import LeaveOneOut   ## LOO 实际上等于 KFold(n, n_folds=n) # scores = cross_val_score(lr, X_arr, y_arr, cv=X_arr.shape[0]) # -- 执行时间非常之长，在 Jupyter 里面运行应该已经超时了，最后没有返回结果 scores = cross_val_score(lr, X_arr, y_arr, cv=1000) # 意思一下…   print("Mean: ", np.mean(scores))  # 0.82   

参考

1. 周志华，《机器学习》
2. 李航，《统计学习方法》
3. 杨治良，《实验心理学》