学习编程之概述—从编程范式开始
作者微信号:sakyayj,目前正在寻找一份数据仓库和数据挖掘的工作
摘要:
与编程语言相比,编程范式要少得多。“少则得,多则惑”,与许多从具体的编程语言开始学习编程的方法不同,本文提供另外一种思路:通过学习编程范式来学习编程,即从少量的编程范式入手,介绍每个范式背后的概念和它们之间的联系。这样使得读者在解决具体问题时,能够选择正确的概念和范式。本文也是我的学习笔记扩展,希望对大家有所帮助。
前言:
回顾自己的编程经历,感觉与其的关系总是若即若离,我发现一个重要的原因就是:以问题为中心,编程作为一个工具是用来解决问题的。而在这个思维框架中,即使是每次亲密接触过程中,我也无法深刻地了解编程,因为我的关注点始终在问题上,比如获得学分,通过等级考试,解决专业问题……甚至为了获得小小的成就感,抑或满足虚荣心。这种情形就像打篮球一样,很多人一上场就满眼全是篮筐,只要将球交给他们,他们下意识的选择就是将篮球投出去,而不去思考如何更加合理地分配球权。每个新的问题都有可能需要新的编程语言、技术或方法。如果仍以问题为中心,随着问题的增多,导致学习编程的成本不断增加,因为在面对新的问题时,利用已有知识仍可能束手无策。因此,对于经常利用编程解决问题的人来说,重新思考编程本身更利于长远发展。
近来时间比较充裕,使得我有整块的时间来关注编程。在学习初始,我相信,在现今五花八门的编程语言和技术(如面向对象、函数编程等)的背后,一定存在某种思想或者框架将这些表象联系起来。就像太极老师说过的一样:“太极拳有很多派别和套路,而真正的拳理只有一个。”“少则得 多则惑”,我相信只要将这些表象恰当地还原到几个点,然后理清它们之间的关系,向外扩展,就能再次得到具体的表象。
带着这种假设,我查找了一些资料,发现编程范式可以作为这个既能被归纳,又能被演绎的“点”。从系统角度来看, 范式也是系统的最大杠杆点。MIT的《Concepts, Techniques, and Models of Computer Programming》(简称CTM,另一本标准化的入门书籍是MIT的《Structure and Interpretation of Computer Programs》,简称SCIP,有人说这两本有交集,我没有看过,所以不评论哪本更好)正符合这种思路,即通过编程范式来理解编程。
正文:
本文主要参考《CTM》和edx上对应的课程。与其他从具体的编程语言来介绍编程的方式不同,这本书是将编程视为一个整体的学科,即编程有两个基本部分:技术(工具)和它的科学基础(概念)。解决一个编程问题要选择正确的概念,对应问题的不同部分需要选择不同的概念,然后才用具体的编程语言(工具)实现。
每个编程范式支持一套概念,在《CTM》中,编程范式定义如下:
“ A programming paradigm is an approach to programming a computer based on a mathematical theory or a coherent set of principles”
这些概念使这个范式最适合解决一类问题。比如面向对象编程适合解决按照一个层次组织的很多相关数据抽象的问题,逻辑编程适合解决根据逻辑规则转换符号结构的问题等。理想情况下,一个编程语言最好支持多种范式,这样就不用增加学习其他编程语言的成本。但实际上却没有一个一招吃遍天下的通用编程语言,主流的语言Java、C++仅支持一到两个单独范式。然而,可以通过理解正确的编程概念可以增进编程样式,比如,即使C语言中,也能写成面向对象的样式。图1中显示了语言、范式和概念之间的关系。

图1
与成百种编程语言相比,编程范式要少得多,如图1所示,共有27种范式。多数范式之间仅相差一个或几个概念,比如图中的函数编程范式,在加入了状态(state)之后就变成了面向对象编程范式。《CTM》强调学习编程从编程范式入手,以基本的范式为起点,然后增加关键概念,得到其它范式,最后形成整个范式图景。
 图2
图2
本文遵循《CTM》的思路,首先介绍编程和编程语言本身,然后介绍5种最常使用的编程范式,如图3所示。具体来说, 从基本的函数编程范式开始,根据现实情况,每次增加一个新的概念(满足创造性扩展原理(creative extension principle) )构成一个新的范式 ,比如因现实世界包含独立活动而增加并发(concurrency)而构成确定数据流编程范式(deterministic dataflow programming ) 、因现实世界不断变化而增加状态(state)而构成面向对象编程范式(object-oriented programming)等。最后介绍语言和程序设计内容,这个话题很大,但这里只是简短说明。
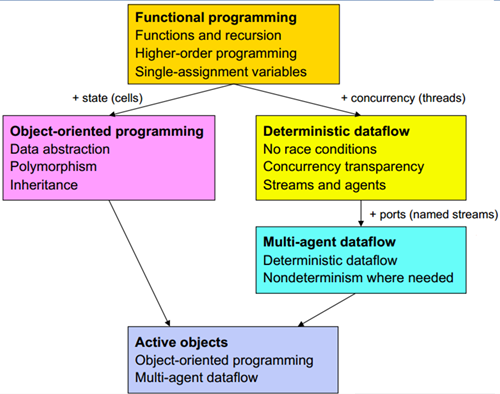 图3
图3
1.编程
编程包含三件事情:
1.一个编程范式:一个定义语言和抽象机和执行语言的形式化系统。
2.一个编程模型:一套使用编程范式的语言写程序的设计技术和原理。比如MapReduce模型
3.一套推理技术:推理程序的正确性和有效性。
首先从第1点中的编程语言谈起,在《语言的故事》,我们了解了自然语言的产生和进化。与自然语言相比,形式语言不是自然进化而来,而是为特定应用而人为设计的。它是更加严格的语法,编程语言就是一种形式语言,从语法来看,与自然语言的对应关系如下:
statement (‘sentence’) = sequence of tokens (‘words’)token (‘word’) = sequence of characters (‘letters’)
同样地,可从句法和语义来定义编程语言。这里使用扩展巴科斯范式(EBNF)来定义语法。EBNF区分终止符和非终止符,一个终止符是一个token,一个非终止符是一系列token。如在图4中的 ::=||定义了非终止符(值)可以是数字、程序或记录。
1.1 句法
EBNF用一套背景无关的语法来描述编程语言,而在现实中,每个编程语言的语法又是背景相关的。比如,很多语言中,变量要在使用前声明,这就是背景相关或依赖。因此,定义句法包含两部分:背景无关语法+一套约束条件。背景无关语法具有歧义, 如23+4,有两个解析树,2(3+4)和(23)+4,最后有两个结果14和10。为了消除歧义,可以增加优先级条件,即先*后+ 。另一个常用的算术运算条件是结合律。函数编程范式的语言句法表达见图4,更为详细的句法表达参见《CTM》的附录C。
 图4
图4
1.2 语义
1.2.1 操作语义
语义定义了程序在执行时应该做什么。理解语义有很多用处:
1.确保程序的正确性
2.确保程序是设计良好的
3.能够给他人解释程序
4.能够计算时间和内存使用
5.能够理解程序如何管理内存
有三种方法定义编程语言的语义,分别是操作语义(operational semantics)、 公理化语义(axiomatic sematics)、指称语义(denotational semantics)和逻辑语义(logical senmantics)。它们只是从不同角度看待程序,分别是抽象机(abstract machine)、含义(implication)、函数(function)和逻辑模型(logical model)。其中操作语义最为通用,可以解释所有范式。
操作语义表达了一个语句是如何按照一个抽象机执行的,它有两部分组成:
1. 核心语言:将实用编程语言转换成核心语言
2. 抽象机:是有一个准确数学定义的简化的计算机
1.2.2 抽象机
定义抽象机的基本概念如下,分为内存、指令和执行三部分:
* 单赋值存储(single-assignment memory) σ={x1=10} :变量和它们所绑定的值;
* 环境(environment) E={X->x,Y->y} :连接标识符和内存中的变量;
* 语义指令(semantic instruction):一个指令和它的环境;
* 语义栈(semantic stack) ST={<s>1,E1,...,(<s>2,E2)} :一个语义指令的栈;
* 执行状态(execution state) (ST,σ) :一个包含一个语义栈和内存的对;
* 执行(execution) (ST0, σ0) ->(ST1, σ1) -> (ST2, σ2)-> · · · :一个执行状态的序列;
1.2.3 正确的程序
下面我们先来看理解语义的第一个好处-程序的正确性。当一个程序按照我们的想法执行正确时,就说明该程序正确。为了证明正确性,要对程序进行推理,包含两件事:
* 语言的语义(language’s semantics):一个告诉程序如何执行的准确的数学模型
* 程序的规范(program’s specification):定义了我们想让程序做的事情
语义是连接规范和程序的桥梁。三者的关系如图5,我们需要证明在程序依据语义执行时,它应该满足规范。
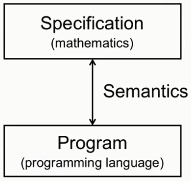 图5
图5
以阶乘为例推导函数的正确性:
1.在规范上:由于该函数是递归函数,所以采用归纳法证明其在数学上的正确性。分为两种f(0)和f(n)两种情形,证明过程略。
2.在程序上:使用语义来推导其正确性:转换核心语言并在抽象机执行。
用scala写出阶乘程序,如下:
defFactorial(N:Int,R:Int){ var N1 =N var N1 =R if(N1 ==0 ) return println(r1.toString()) else R1= N1* R1 N1= N1- 1 Factorial5( N1, R1) } 首先,将程序Factorial()转换成核心语言,
proc{Factorial N R} local B N1R1in N1=N R1=R B=(N1==0) if B then print() else R1=N1*R1 N1=N1-1 Factorial5( N1, N1) end end end 函数Factorial没有返回值,是程序(procedure)。核心语言的if语句的条件必须用标识符作为参数,而不能用表达式,所以要引入b。同样地,为了在else中做计算一般情况的n*(n-1),要引入两个标识符n1和r1。每一核心语言都足够简单,以便表达明确的语义。
然后,在抽象机执行程序的核心语言,分为Factorial(0)和Factorial(n)两种情况,只说明前者的执行情况,后者详见《CTM》:
1.准备:当n=0时,执行前准备一个内存σ存储程序值(程序的定义+背景相关的环境)和一个环境E连接程序和内存:σ ={factorial=proc{$ N R}…end,{Factorial ->factorial },n=0,r}, E={Factorial->factorial,N->n,R->r}。然后执行Factorial( N R),E,σ;
2.用程序的核心语言本身代替Factorial( N R);
3.执行local语句:
local B N1R1in N1=N R1=R B=(N1==0),E,σ
包含两个操作:1)在内存中新增三个变量b,n1,r1;2)在环境中新增{B->b,N1->n1,R1->r1}。变为:
local B N1R1in N1=N R1=R B=(N1==0),E={Factorial->factorial,N->n,R->r,B->b,N1->n1,R1->r1 } ,σ∪{b}∪{n1}∪{r1} 4.绑定值:当n=0时,依次绑定值为,local中的n1=0,r=1,r1=1。再绑定b=true,输出最终结果。至此完成了整个factorial(0)的验证过程。
写到这里,清理下头脑回头看看,感觉还是会有很多地方没写清楚,这与本人的表达能力和写作水平欠佳有关。如果您想要了解关于本文的更多内容,可以与我交流,或者直接阅读《CTM》。











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

