转载

如何利用参数和非参数方法来检测异常值

异常值是指距离其他观测值非常遥远的点，但是我们应该如何度量这个距离的长度呢？同时异常值也可以被视为出现概率非常小的观测值，但是这也面临同样的问题——我们要如何度量这个概率的大小呢？

有许多用来识别异常值的参数和非参数方法，参数方法需要一些关于变量分布情况的假设条件，而非参数方法并不需要这些假设条件。此外，你还可以利用单变量分析和多变量分析的方法来识别异常值。

那么问题来了，哪个方法得到的结果才是正确的呢？不幸的是，实际上并不存在唯一的标准答案，结果的正确与否取决于你识别这些异常值的目的。你可能想要单独分析某个变量的情况，或者想利用这些变量构建预测模型。

让我们采用更直观的方法来识别异常值吧。

假设存在一个关于移动应用程序的数据集，其中包括操作系统、用户收入和设备情况三个变量，如下图所示：

我们应该如何识别出收入变量的异常值呢？接下来我将尝试利用参数和非参数方法来检测异常值。

参数方法

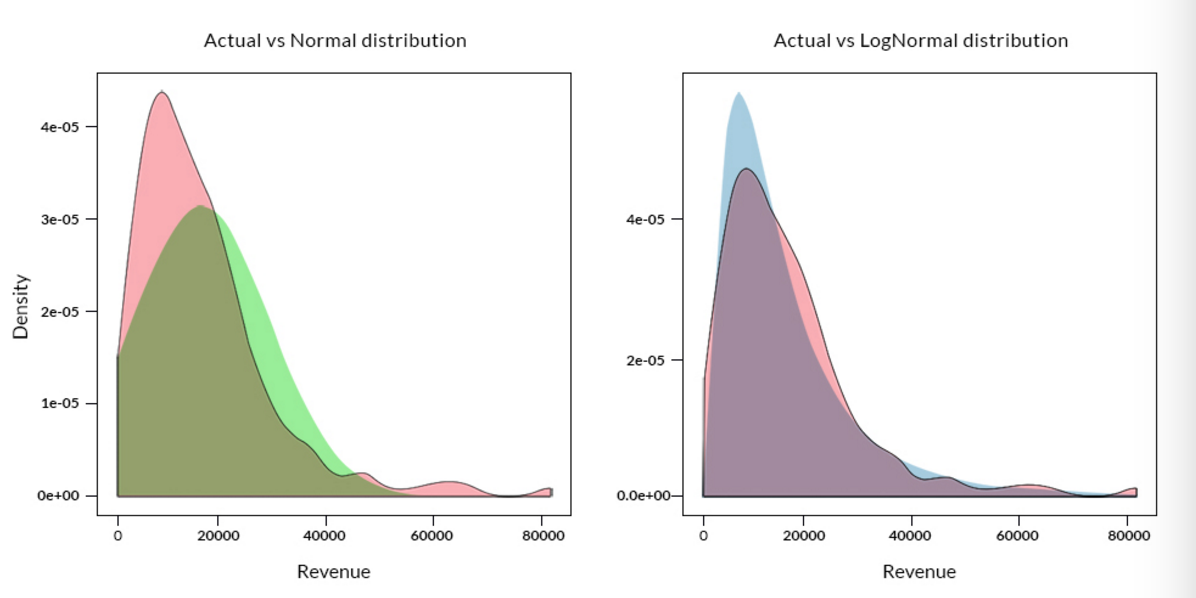如何利用参数和非参数方法来检测异常值如上图所示，x轴中的变量是收入，y轴代表收入值对应的概率密度值。图中粉色部分代表真实的样本数据，绿色部分表示正态分布数据，蓝色部分代表对数正态分布数据。其中正态分布和对数正态分布数据与实际样本数据具有相同的均值和方差。

我们可以通过计算观测值出现的概率或者计算观测值与均值之间的距离来判断异常值的情况。比如，正态分布情况下位于距均值三倍标准差范围外的观测值被视为异常值。

上述的例子中，如果我们假设原始数据服从正态分布，那么收入大于60,000元的数据都被视为异常值。从右图中可以看出，对数正态分布能更好地识别出真实的异常值，这是因为原始数据的分布近似于服从对数正态分布。但这并不是一个通用的方法，因为我们很难事先判断出数据潜在的分布情况。我们可以通过数据的拟合曲线来判断参数情况，但是如果原始的数据发生了变化，那么分布的参数也会随之发生改变。

上图展示了概率密度函数如何随参数的变化而发生改变，我们可以很明显地看出参数的变化会影响异常值的识别过程。

非参数方法

首先让我们来看一个识别异常值的简单的非参数方法——箱线图：

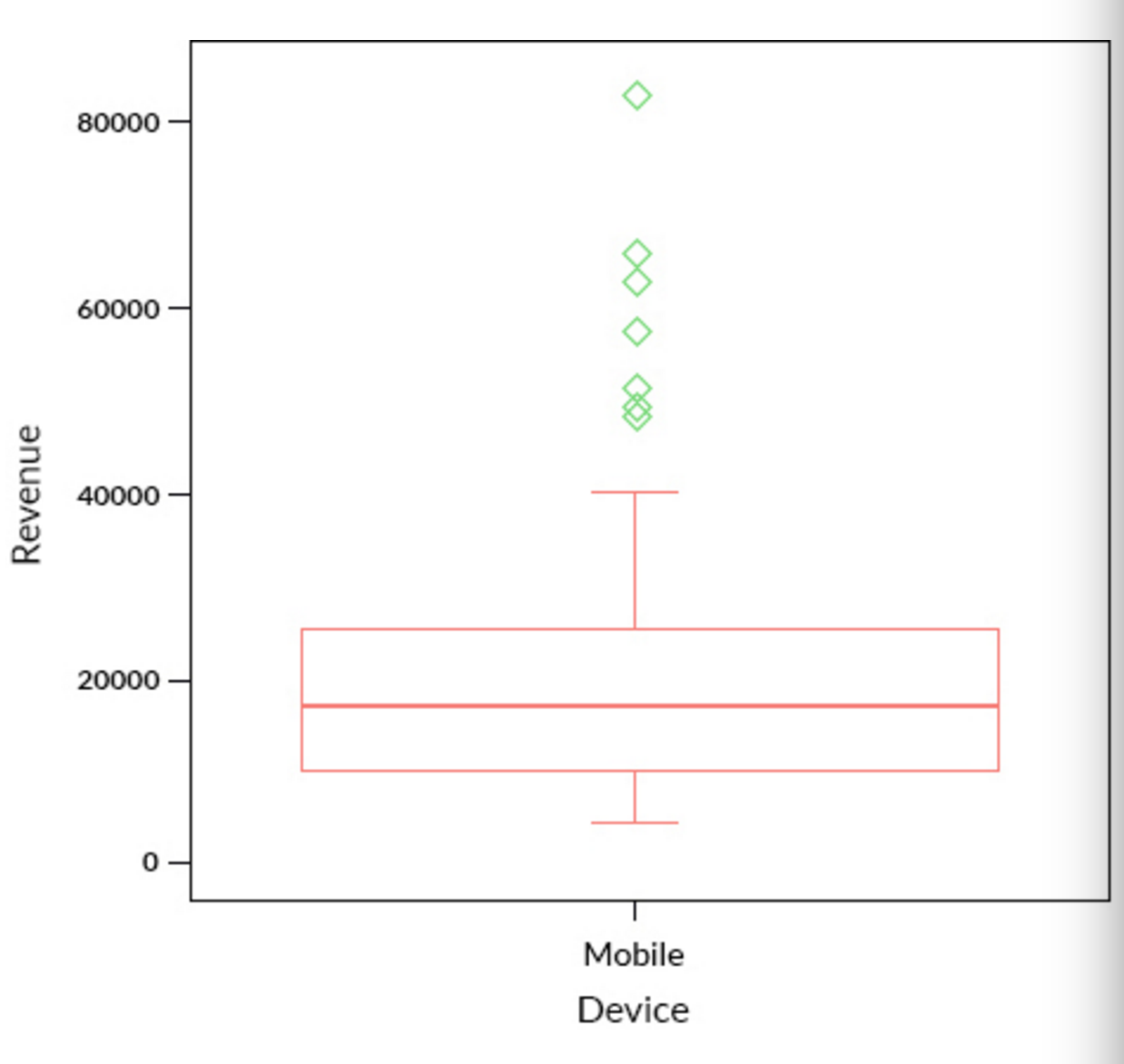
如上图所示，我们可以看出数据中存在 7 个显著的异常值(绿色标记的数据)。更多关于箱线图的内容请参考这篇文章。

上文提到的数据集中还存在一个分类变量——操作系统。如果我们根据操作系统将数据分组并绘制箱线图，那么我们是否能够识别出相同的异常值呢？

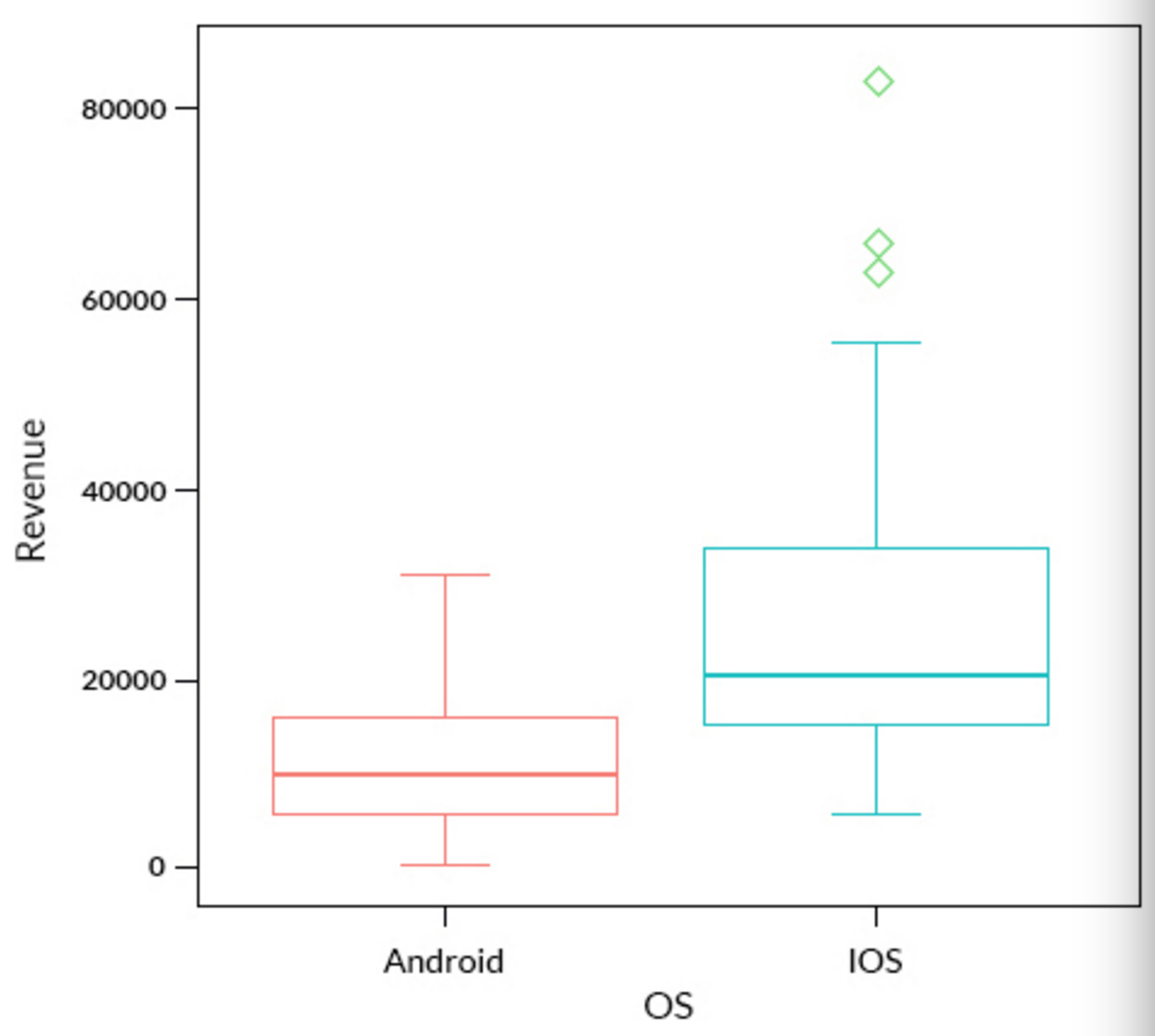
上图中，我们采用了多变量分析的方法。从图中我们可以看出，IOS 组中存在 3 个异常值，而安卓组则没有检测出异常值。这是因为安卓用户和 IOS 用户的收入分布情况不一致，所以如果只利用单变量分析方法的话，我们将会错误地识别出异常值。

结论

我们可以利用基于数据潜在分布情况的参数和非参数方法来检测异常值。在样本数据的均值十分贴近于分布函数的中心且数据集足够大的情况下，我们可以利用参数方法来识别异常值。如果中位数比均值更贴近于数据的分布中心，那么我们应该利用非参数的方法来识别异常值。在第二部分中，我将介绍如何通过多变量分析方法——聚类方法(一个常用的数据挖掘技术)——来识别异常值。

原文作者： Jacob Joseph

原文链接： https://blog.clevertap.com/how-to-detect-outliers-using-parametric-methods-and-non-parametric-methods/

译者：Fibears

原文 http://datartisan.com/article/detail/100.html

正文到此结束