《每周一点canvas动画》——三角函数(2)

在上一节我们介绍了canvas动画中有关三角函数的内容，以及一个跟随鼠标旋转的箭头动画。那么，在这一节呢！介绍的内容比较多，包括：

• 波形运动

• 圆周运动

• 两点间的距离

一.波形运动

sin函数的波形想必骚年们不会感到陌生，如果只是考虑一个周期以内的函数波形，如下图所示：

如果我们想要去到sin函数在[0, 2π]之间的值，非连续的情况下，可以这样估算：

    for(var angle=0; angle<Math.PI*2; angle+=0.1){         console.log(Math.sin(angle)); //打印出角度对应的sin值     }

那么，它能做什么呢？别急，这里我们首先新建一个类，文件名为 ball.js ,顾名思义这是一个球体，我们将要通过它来表现不同的运动形态。这样，包括上一节中的箭头文件 arrow.js ，在你的js文件中就有两个类文件了：

• js

  • arrow.js

  • ball.js

ball.js代码具体如下，这里就不做过多解释了。我们只是画了一个圆。

ball.js文件      function Ball(radius,color){         if(radius === undefined) {radius = 40;}         if(color === undefined){color = '#00ff00';}         this.x = 0;         this.y = 0;         this.vx = 0;         this.vy = 0;         this.radius = radius;         this.rotation = 0;         this.mass = 1;         this.scaleX = 1;         this.scaleY = 1;         this.color = utils.parseColor(color);         this.lineWidth = 1;      }      Ball.prototype.draw = function(context){         context.save();         context.translate(this.x,this.y);         context.rotate(this.rotation);         context.scale(this.scaleX,this.scaleY);         context.lineWidth = this.lineWidth;         context.fillStyle = this.color;         context.strokeStyle = this.color;         context.beginPath();         context.arc(0,0,this.radius,0,Math.PI*2,false);         context.closePath();         context.fill();         context.stroke();         context.restore();     }

1.平滑运动(Smooth motion)

这里我们首先介绍Math,sin(angle)的第一个应用——平滑运动。平滑(smoothly)这个词的意思是指物体的一种流畅的运动状态，与之相反的是机械式的简单的从0到1再到-1和0的这么一种状态。平滑的运动更加趋近与自然的运动状态，类似水草在水流中的左右摇摆，在摆动的过程中是有速度的变化的。我们用sin函数模仿的第一个运动，就是这种类似水草摆动的运动。另外，因为sin函数的值是在[-1,1]之间。所以在实际代码中需要乘以一个较大的值(也就是振幅，你懂得)，使其的摆动看起来明显一些。具体代码如下：

  <canvas id="canvas" width="500" height="500" style="background:#000009;">        your browser not support canvas!    </canvas>    <script src="../js/utils.js"></script>    <script src="../js/ball.js"></script>    <script>        window.onload = function(){            var canvas = document.getElementById("canvas");            var context = canvas.getContext("2d");             var ball = new Ball();                   ball.x = canvas.width/2;                   ball.y = canvas.height/2;             var angle = 0,                range = 50; //振幅             (function drawFram(){                window.requestAnimationFrame(drawFram,canvas);                context.clearRect(0,0,canvas.width,canvas.height);                 ball.x = canvas.width/2 + Math.sin(angle)*range; //核心                angle += 0.1;                 ball.draw(context);            })();        }     </script>

这样你就可以看到一个在canvas画布中心左右摇摆的球，相比于机械的加减是不是更加的流畅呢？当然，你也可以控制摆动的速度，怎么做呢？很简单 angle += speed ,将speed设置为任意大小的值就可以了。当然，如果你想让它做垂直运动只需要变化 ball.y 即可。

2.线性运动(Linear motion)

线性运动是最简单的一种运动，物体匀速朝某个方向运动，就是线性运动。这里直接给你具体代码：

<canvas id="canvas" width="500" height="500" style="background:#000;">        you browser not support canvas!    </canvas>    <script src="../js/utils.js"></script>    <script src="../js/ball.js"></script>    <script>        window.onload = function(){            var canvas = document.getElementById('canvas'),                  context = canvas.getContext('2d');            var angle = 0,                range = 50,                xspeed = 1,                yspeed = 0.05;             var ball = new Ball();                        (function drawFrame(){                window.requestAnimationFrame(drawFrame,canvas);                context.clearRect(0,0,canvas.width,canvas.height);                 ball.x += xspeed; //水平，沿x轴方向水平运动                                if(ball.x > canvas.width + ball.radius){                    ball.x = -ball.radius;                }                //垂直， 由于angle角度没发生变化，所以纵坐标保持不变                ball.y = canvas.height/2+Math.sin(angle)*range;                               // angle += 0.05; //取消注释看看发生了什么？                ball.draw(context);            })();        }     </script>

其实，这里如果你把 angle += 0.05 取消注释，你会发现球的运动轨迹就与sin函数的图像一致了。

3.脉冲运动(Pulsing motion)

脉冲运动是将sin函数运用于物体大小的变化中，具体代码如下：

window.onload = function(){             var canvas = document.getElementById('canvas');             var context  = canvas.getContext('2d');              var angle = 0,                 range = 0.5,                 speed = 0.05,                 centerScale = 1;              var ball = new Ball();                 ball.x = canvas.width/2;                    ball.y = canvas.height/2;              (function drawFrame(){                 window.requestAnimationFrame(drawFrame,canvas);                 context.clearRect(0,0,canvas.width,canvas.height);                                  //sin值的变化，导致 ball.scaleX ， ball.scaleY属性变化                 ball.scaleX = ball.scaleY = centerScale + Math.sin(angle)*range;                 angle += speed;                  ball.draw(context);             })();         }

由此你应该知道，除了位置属性，我们还可以将sin函数与其他的属性相结合，来形成不同的运动形式。

在上面的代码中，我们几乎都是在球体的某一个属性上做出变动。当然，你也可以试一试同时在ball.x 和ball.y上运用sin函数，看看又能得到什么样的结果！sin函数的使用方法已经交给你了，到底能创造出什么样意想不到的作品就看你的了。

二、圆周运动

圆周运动可以分为两种形式： 正圆运动 和 椭圆运动
在将圆周运动之前，各位骚年们，一大波数学公式正在向我们袭来。请护好自己的膝盖，听不懂没关系，只要记住程序怎么写就好了，能懂是最好的，这对后面学习高级动画是很有帮助的。好吧，那我就废话少说直接上菜了：

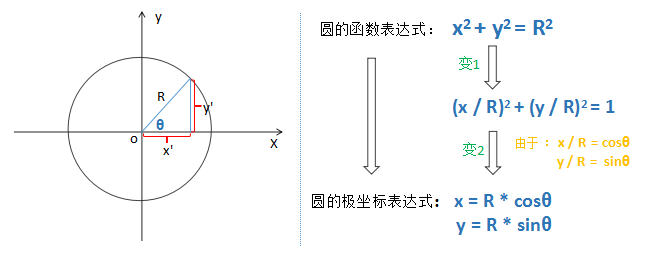
1.正圆运动

上图展示了从圆的函数表达式到圆的极坐标表达式之间的转换过程。理解不理解都没有关系，总之你要明白，最终我们将 x, y 与 sin 和 cos 扯上关系了。而圆的极坐标表达式就表示的是一个圆。这样我们想要让一个物体做圆周运动，那不就so easy了吗？具体代码如下：

    window.onload = function(){                var canvas = document.getElementById('canvas'),                    context = canvas.getContext('2d');                 var ball = new Ball();                 var angle = 0, // 旋转的角度                    centerX = canvas.width/2,                    centerY = canvas.height/2,                    radius = 100, // 定义半径                    speed =0.05; // 每帧旋转角度的增加值                 (function drawFrame(){                    window.requestAnimationFrame(drawFrame, canvas);                    context.clearRect(0,0,canvas.width, canvas.height);                     //centerX, centerY 的作用是让球绕画布中心旋转                    ball.x = centerX + Math.sin(angle)*radius;                    ball.y = centerY + Math.cos(angle)*radius;                     //角度增加                    angle += speed;                    ball.draw(context);                }());            }

ok,自己动手试试吧！看看是不是球体绕着画布中心做着圆周运动呢！这里我们需要的条件比较多 angle 和 R，在后面的章节中我们将介绍如何只通过 angle 就实现圆周运动。为了更容易理解，我劝你最好复习一下中学的知识，哈哈！！！

2.椭圆运动

椭圆和正圆的不同之处可以这样理解： 正圆半径在x轴和y轴上的距离是相同的，都是Radius.而椭圆则是不同的,我们用a, b 表示。

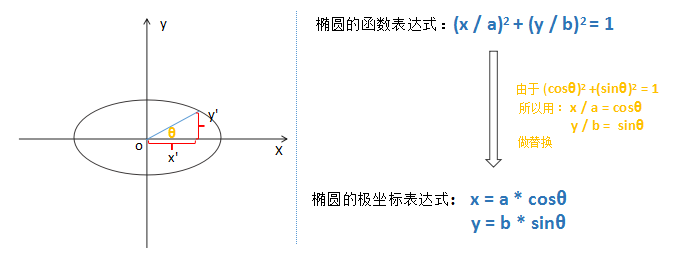
具体到代码里，就是半径不同了呗！是不是so easy,上代码：

window.onload = function(){             var canvas = document.getElementById('canvas');             var context = canvas.getContext('2d');             var ball = new Ball();                          var centerX = canvas.width/2,                 centerY = canvas.height/2,                 angle = 0,                 radiusX = 50,                 radiusY = 100,                 speed = 0.05;                              ball.x = centerX;                 ball.y = centerY;                          (function drawFrame(){                 window.requestAnimationFrame(drawFrame,canvas);                 context.clearRect(0,0,canvas.width,canvas.height);                                  //当radius的值相等时为圆周运动                 //当radius的值不想等是为椭圆运动                 ball.x = centerX + Math.sin(angle)*radiusX; //radiusX = 50                 ball.y = centerY + Math.cos(angle)*radiusY; //radiusY = 100                 angle += speed;                                  ball.draw(context);             })();         }

哎！好累！！！

三、两点之间的距离

按理来说，连点之间的距离是不会用到三角函数的。但是，其实两点间的距离公式是可以通过勾股定理推出来的，所以这里直接就把他归到三角函数里。这里就不画示意图了直接给你个公式好了(原谅我偷个懒)，假设有两个点, a(x1, y1), b(x2, y2)。那么怎样求它们之间的距离呢！公式如下：

    dx = x2 - x1;     dy = y2 - y1;     distance = Math.sqrt(dx*dx + dy*dy); //这不就是勾股定理

这里给你个小的Demo,代码如下：

    <canvas id="canvas" width="500" height="500" style="background:#000;">            your browser not support canvas!        </canvas>        <p id="log"></p>        <script src="../js/utils.js"></script>        <script>        window.onload = function(){                var canvas = document.getElementById('canvas');                var log = document.getElementById('log');                var mouse = utils.captureMouse(canvas);                var context = canvas.getContext('2d');                 //中心位置创建一个方块                var rect = {                    x:canvas.width/2,                    y:canvas.height/2                };                 (function drawFrame(){                    window.requestAnimationFrame(drawFrame,canvas);                    context.clearRect(0,0,canvas.width,canvas.height);                     var dx = mouse.x - rect.x;                    var dy = mouse.y - rect.y;                    var dis = Math.sqrt(dx*dx + dy*dy);                     //画方块                    context.fillStyle = '#ffffff';                    context.fillRect(rect.x-2,rect.y-2,4,4);                    //画线                    context.save();                    context.strokeStyle = '#ffffff';                    context.beginPath()                    context.moveTo(rect.x,rect.y);                    context.lineTo(mouse.x,mouse.y);                    context.closePath();                    context.stroke();                    context.restore();                    //显示距离                    log.style.left = (mouse.x + rect.x)/2 + 'px';                    log.style.top = (mouse.y + rect.y)/2 + 'px';                    log.innerHTML = dis;                })();            }     </script>

四、总结

哈哈，来给本章的重要公式做一个总结，我真是好人呐：

    ## 角度旋转     dx = mouse.x - object.x;     dy = mouse.y - object.y;     object.rotation = Math.atan2(dy,dx)*180/Math.PI      ## 平滑运动        value = center + Math.sin(angle)*range;        angle += speed;      ## 正圆运动        x_position = centerX + Math.sin(angle)*radius;        y_position = centerY + Math.cos(angle)*radius;        angle += speed;      ## 椭圆运动        x_position = centerX + Math.cos(angle)*radiusX;        y_position = centerY + Math.sin(angle)*radiusY;        angle += speed;      ##两点间距离     dx = x2 - x1;     dy = y2 - y1;     dist = Math.sqrt(dx*dx + dy*dy); 

写完这篇，我已泣血而亡，各位小主麻烦点个赞吧！！！