转载

数据结构学习笔记（六）链表算法题

假期结束，看点题目。

第一题

问题

设顺序表用数组A[]表示，表中元素存储在数组下标1~m+n的范围内，前m个元素递增有序，后n个元素递增有序，设计一个算法，使得整个顺序表有序。

（1）给出算法的基本设计思想。

（2）根据设计思想，采用C或C++语言描述算法，关键之处给出注释。

（3）说明你所设计算法的时间复杂度和空间复杂度。

解答

（1）算法基本设计思想：

将数组A[]中的m+n个元素（假设元素为int型）看成两个顺序表，表L和表R。将数组当前状态看做起始状态，即此时表L由A[]中前m个元素构成，表R由A[]中后n个元素构成。要使A[]中m+n个元素整体有序只需将表R中的元素逐个插入表L中的合适位置即可。插入过程：取表

R中的第一个元素A[m+1]存入辅助变量temp中，让temp逐个与A[m],A[m-1],…,A[1]进行比较，当temp<A[j]（1≤j≤m）时，将A[j]后移一位；否则将temp存入A[j+1]中。重复上述过程继续插入A[m+2],A[m+3],……,A[m+n]，最终A[]中元素整体有序。

（2）算法描述

void Insert(int A[],int m,int n){  int i,j;  int temp; //辅助变量，用来暂存待插入元素。  for(i=m+1;i<=m+n;i++) { //将A[m+1…m+n]插入到A[1…m]中。  temp=A[i];  for(j=i-1;j>=1&&temp<A[j];j--)   A[j+1]=A[j]; //元素后移，以便腾出一个位置插入temp。  A[j+1]=temp; //在j+1位置插入temp。  } }

（3）算法时间和空间复杂度

①本题的规模由m和n共同决定。取最内侧循环中A[j+1]=A[j];这一句作为基本操作，其执行次数在最坏的情况下为：f(m,n)=(m+m+n-1)n/2=mn+n2/2–n/22

②算法额外空间中只有一个变量temp，因此空间复杂度为O(1)。

第二题

问题

已知递增有序的单链表A,B（A,B中元素个数分别为m,n且A,B都带有头结点）分别存储了一个集合，请设计算法以求出两个集合A和B的差集A-B（即仅由在A中出现而不在B中出现的元素所构成的集合）。将差集保存在单链表A中，并保持元素的递增有序性。

（1）给出算法的基本设计思想。

（2）根据设计思想，采用C或C++语言描述算法，关键之处给出注释。

（3）说明你所设计算法的时间复杂度。

解答

（1）算法基本设计思想：只需从A中删去A与B中共有的元素即可。由于两个链表中元素是递增有序的所以可以这么做：设置两个指针p, q开始时分别指向A和B的开始结点。循环进行以下判断和操作，如果p所指结点的值小于q所指结点值，则p后移一位；如果q所指结点的值小于p所指结点的值，则q后移一位；如果两者所指结点的值相同，则删除p所指结点。最后p与q任一指针为NULL的时候算法结束。

（2）算法描述：

void Difference(LNode *&A, LNode *B) {  LNode *p = A->next, *q = B->next; //p和q分别是链表A和B的工作指针。  LNode *pre = A;  LNode *r;  while(p != NULL && q != NULL) {   if(p->data < q->data) {    pre = p;   //pre 为A中p所指结点的前驱结点的指针。    p = p->next;  //A链表中当前结点指针后移。   }   else if (p->data > q->data)    q = q->next;   else {    pre->next = p->next; //B 链表中当前结点指针后移。    r = p; //处理A，B中元素值相同的结点，应删除。    p = p->next;    free(r); // 删除结点。   }  } }

（3）算法时间复杂度分析：由算法描述可知，算法规模由m和n共同确定。算法中有一个单层循环，循环内的所有操作都是常数级的，因此可以用循环执行的次数作为基本操作执行的次数。可见循环执行的次数即为p, q两指针沿着各自链表移动的次数，考虑最坏的情况，即p, q都走完了自己所在的链表，循环执行m+n次。即时间复杂度为O(m+n)。

第三题

问题

设计一个算法，将顺序表中的所有元素逆置。

解答

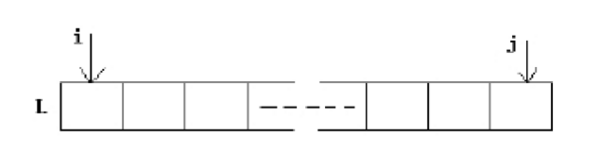
数据结构学习笔记（六）链表算法题

两个变量i，j指示顺序表的第一个元素和最后一个元素，交换i，j所指元素，然后i向后移动一个位置，j向前移动一个位置，如此循环，直到i与j相遇时结束，此时顺序表L中的元素已经逆置。

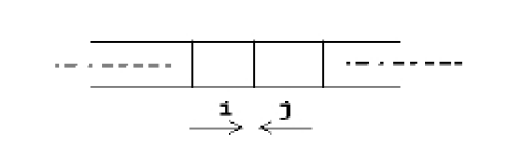
void reverse(Sqlist &L) {  //L要改变，用引用型  int i,j;  int temp; //辅助变量，用于交换  for(i=1,j=L.length;i<j;i++,j--) {  //当i与j相遇时循环结束   temp=L.data[i];   L.data[i]=L.data[j];   L.data[j]=temp;  } }

注意：本题中 for 循环的执行条件要写成 i < j 而不要写成 i != j 。如果数组中元素有偶数个则 i 与 j 会出现下图所示状态，此时i 继续往右走，j 继续往左走，会互相跨越对方，循环不会结束。

数据结构学习笔记（六）链表算法题

第四题

问题

设计一个算法，从一给定的顺序表L中删除下标i到j（i≤j，包括i，j）之间的所有元素，假定i,j都是合法的。

解答

本题是顺序表删除算法的扩展，可以采用如下方法解决，从第j+1个元素开始到最后一个元素为止，用这之间的每个元素去覆盖从这个元素开始往前数第j-i+1个元素，即可完成删除i~j之间的所有元素。

本题代码如下：

void Delete(Sqlist &L,int i,int j) { //L要改变，用引用型。  int k,l;  l = j-i+1; //元素要移动的距离。  for(k = j + 1;k <= L.length; k++) {   L.data[k-l] = L.data[k]; //用第k个元素去覆盖它前边的第l个元素。  }  L.length -= l; //表长改变。 }

第五题

问题

有一个顺序表L，其元素为整型数据，设计一个算法，将L中所有小于表头元素的整数放在前半部分，大于的整数放在后半部分，数组从下表1开始存储。

解答

本题可以这样解决，先将L的第一个元素存于变量temp中，然后定义两个整型变量i,j。i从左往右扫描，j从右往左扫描。边扫描边交换。具体执行过程如下：

各步的解释如下：

①开始状态， temp = 2,i = 1; j = L.length

②j先移动，从右往左，边移动边检查j所指元素是否比2小，此时发现-1比2小，则执行 L.data[i]=L.data[j];i++; （i中元素已经被存入temp所以可以直接覆盖，并且i后移一位，准备开始i的扫描）

③i开始移动，从左往右，边移动边检测，看是否i所指元素比2大，此时发现-7比2小，因此i在此位置是什么都不做。

④i继续往右移动，此时i所指元素为-3也比2小，此时什么都不做。

⑤i继续往右移动，此时i所指元素为5，比2大，因此执行 L.data[j] = L.data[i]; j-- （j中元素已被保存，j前移一位，准备开始j的扫描）

⑥j往左运动，此时j所指元素为6，比2大，j在此位置时，什么都不做。

⑦j继续往左移动，此时j==i，说明扫描结束。

⑧执行 L.data[i] = temp; 此时整个过程结束，所有比2小的元素被移到了2前边，所有比2大的元素被移到了2后边。

以上过程要搞清楚两点：

①i和j是轮流移动的，即当i找到比2大的元素时，将i所指元素放入j所指位置，i停在当前位置不，j开始移动。j找到比2小的元素，将j所指元素放在i所指位置，j停在当前位置不动，i开始移动如此交替直到i==j。

②每次元素覆盖（比如执行 L.data[i] = L.data[j]; ）不会造成元素丢失，因为在这之前被覆盖位置的元素已经存入其他位置。由以上分析可写出如下算法：

void move(Sqlist &L) { //L要改变所以用引用型  int temp;  int i = 1,j = L.length;  temp = L.data[i];  while(i<j){   /*关键步骤开始*/   while(i < j&&L.data[j] > temp)     j--;     //j从左往右扫描，当来到第一个比temp小的元素时停止  ,并且每走一步都要判断i是否小于j,这个判断容易遗漏。   if(i < j) { //检测看是否已仍满足i < j，这一步同样很重要    L.data[i] = L.data[j]; //移动元素。    i++; //i右移一位。   }   while(i < j&&L.data[i] < temp) i++; //与上边的处理类似。   if(i < j) { //与上边的处理类似。    L.data[j] = L.data[i]; //与上边的处理类似。    j--;   }   /*关键步骤结束*/  }  L.data[i] = temp; //将表首元素放在最终位置。 }

正文到此结束