SICP 第四章总结
本书的前三章分别讨论了 数据抽象 、 过程抽象 、 模块化 三种程序设计的技术,这些都是编程的问题,一直采用的是 Scheme 作为编程语言。如果遇到的问题更复杂,或者需要解决某领域的大量问题,有可能发现现实可用的语言(Lisp,或其他)都不够满意或不够方便,因此第四章主要就是讲述如何设计和实现一门新语言。
第四章首先介绍了一个解释器(本书中文翻译为“求值器”)最核心的部分(eval与apply),然后基于这个核心,做了一系列的扩展,下面让我们一起回顾总结下。
元语言抽象
4.1 小节告诉我们 语言的解释器自身也是一个过程 而已,送给它的输入是相应语言的表达式(即程序),它就会完成该表达式要求做的动作。所以我们完全可以用 Scheme 写出一个 Scheme 的解释器,学习求值器实现,有助于理解语言本身和语言实现中的问题。而且 Scheme 语言有强大的符号处理能力,特别适合用于做这种工作。
在阅读4.1章节之前,我用 Java 尝试实现了一个 Scheme 解释器 JCScheme,之前也写过文章介绍,最核心的就是下面两个过程:
- eval 在一个环境里的求值一个表达式
- apply 将一个过程对象应用于一组实际参数

表达式在环境中的求值被规约到过程对实际参数的应用,而这种应用又被规约到新的表达式在新的环境中的求值,如此下去,直到下降到符号(其值可以在环境中找到)或者基本过程(它们可以直接应用)。
后面的 amb 解释器、查询语言的解释器都是在这个基本循环的基础上改造来的。
图灵机
4.1.5 小节中,将程序看成一种抽象的机器的一个描述,按照这种观点,求值器可以看作一部非常特殊的机器,它要求以一部机器的描述作为输入,给定了一个输入后,求值器就能够规划自己的行为,模拟被描述机器的执行过程。
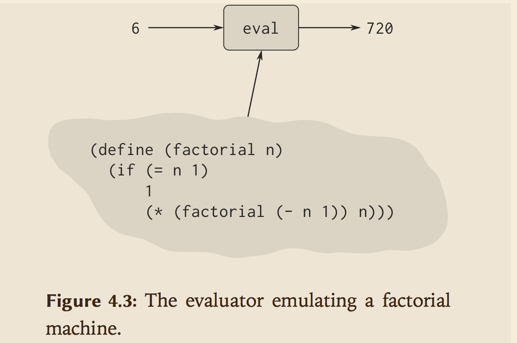
任一求值器都能够模拟其他的求值器
这样,有关“原则上说什么可以计算(忽略掉时间与空间的实践性问题)”的概念就是与语言或者计算机无关了,它反映的是一个有关 可计算性 的基本概念。图灵1936年的论文阐述了这个问题,并声称:
任何“有效过程”都可以描述为这种机器的一个程序
而后图灵实现了一台通用机器,即一台图灵机,其行为就像是所有图灵机程序的求值器。
这一求值器是违反直觉的,因为它是由一个相对简单的过程实现,却能去模拟可能比求值器本身还复杂的各种程序,通用求值器的存在是计算的一种深刻而美妙的性质。递归论是数理逻辑的一个分支,这一理论研究计算的逻辑极限, 《GEB》 里也探讨了一些思想,有兴趣的可以把这本书加入书单。
其他领域中也有这种通用功能的东西,像电子书、音乐播放器等都属于“专用的通用设备”,计算机(一个编程语言就是一种抽象的计算机)比它们更进一步:它能模拟自己。
这里比较有意思的是 习题4.15 的停机问题,本小节所有解释器的代码可以参考 main.scm 。
JIT
4.1.7小节中将语法分析与执行分开,这里的做法类似于高级语言的解释和编译:
- 直接解释,就是一遍遍分析程序代码,实现其语义。例如最早的 BASIC 语言实现
- 编译把实现程序功能的工作分为两步:
- 通过一次分析生成一个可执行的程序
- 在此之后可以任意地多次执行这个程序
这里做的是从 Scheme 源程序(元循环解释器/求值器处理的“数据”)到 Scheme 可执行程序的翻译,这是一种 Just In-time Translation,JIT(即时翻译) ,目前成熟的Java虚拟机都采用这种技术来提高执行效率。在实际中应用,还需进一步考虑整体效率问题。
惰性求值
4.1 小节实现的求值器采用的应用序求值(过程应用之前完成对所有参数的求值),4.2 小节修改之前的求值器,使之能够按照正则序求值,也称为惰性求值。惰性求值的可以用来实现第三章介绍的流,而且也可以避免下面的问题:
(define (tryab) (if(=a0) 1 b)) (try0(/10)) # 如果采用正则序,这里不会抱错,因为 try 函数中根本就没用的b的值
这里要做的修改不是很多,只是在过程的参数上包一层,加一个 trunk ,真正需要计算时在求值,核心代码可以参考 trunk.scm ,此外,处于性能方便的考虑,一般会对求过的参数进行缓存。
我自己实现的 JCScheme 也支持这种正则序求值,感兴趣的 参考 。
amb 非确定性计算
amb 的名字来自 ambiguous(歧义,多义),4.3小节在 Scheme 里扩充非确定性计算功能。非确定性计算里最关键的思想:
- 允许一个表达式有多个可能的值
-
在求值这种表达式时,求值器可以自动选出一个值可能从可以选的值中任意选出一个。还需要维持与选择相关的轨迹(知道哪些元素已经选过,哪些没选过。在后续计算中要保证不出现重选的情况)
-
如果已做选择不能满足后面的要求,求值器就会回到有关的表里再 次选择,直至求值成功;或者所有选择都已用完时求值失败
非确定性计算的过程将通过求值器自动进行的搜索实现,选择和重新选择的方法和实际过程都隐藏在求值器的实现里,程序员不需要关心,不需要做任何与之相关的事情,这一修改的意义深远,语言扩充了,语义有重要改变。
非确定性计算与流处理
非确定性求值和流处理有相似的地方,现在比较一下非确定性求值和流处理中时间的表现形式:
-
流处理中,通过惰性求值,松解潜在的(有可能是无穷的)流和流元素 的实际产生时间之间的紧密联系
- 造成的假象是整个流似乎都存在
- 元素的产生并没有严格的时间顺序
-
非确定性计算的表达式表示对一批“可能世界”的探索
- 每个世界由一串选择确定
- 求值器造成的假相:时间好像能分叉
- 求值器保存着所有可能的执行历史
- 计算遇到死路时退回前面选择点转到另一分支,换一个探索空间
continuation 继续
“继续”是一种过程参数,它总是在过程的最后一步调用。带有“继续”参数的过程不准备返回,过程的最后一步是调用某个“继续”过程。“继续”是“尾调用”,调用过程的代码已经全部执行完毕。
amb 分析器产生的执行过程要求三个参数:
- 一个环境
- 一个成功继续
- 一个失败继续
执行过程的体求值结束前的最后一步总是调用这两个过程之一
- 如果求值工作正常完成并得到结果,就调用由“成功继续”参数 得到的那个过程
- 如果求值进入死胡同,就调用“失败继续”参数过程
(lambda (env succeed fail) ;; succeed is a (lambda (value fail) ...) ;; fail is a (lambda () ...) ...)
这里需要注意的是要恢复破坏性操作(如赋值等),必须设法保存恢复信息。
(define(analyze-assignmentexp) (let((var(assignment-variableexp)) (vproc(analyze(assignment-valueexp)))) (lambda(envsucceed fail) (vprocenv (lambda(valfail2) (let((old-value(lookup-variablevar env))) (set-variable-value!var val env) (succeed'ok (lambda() (set-variable-value!var old-value env) (fail2))))) fail))))
amb 求值器的完整代码可以参考 main-amb.scm 。
逻辑程序设计
本书一开始就强调了:
数学处理说明式知识;计算机科学处理命令式知识
程序语言要求用算法的方式描述解决问题的过程,大多数程序语言要求用定义数学函数的方式组织程序:
- 程序要描述“怎么做”的过程
- 所描述的计算有明确方向,从输入到输出
- 描述经计算的表达式,给出了从一些值算出结果的方法(和过程)
- 定义过程描述如何从参数计算出结果
但是也有例外,第三章介绍的约束传递系统中的计算对象是约束关系,没有明确计算方向和顺序,它的基础系统要做很多工作以支持相应的计算。4.3小节的非确定性程序求值器里的表达式可有多个值,求值器设法根据表达式描述的关系找出满足要求的值。
逻辑程序设计可看作上面想法的推广,一个“是什么”的描述可能蕴涵许多“怎样做”的过程。考虑 append:
(define(appendx y) (if(null?x) y (cons(carx)(append(cdrx)y))))
可认为,这个程序表达了两条规则:
- 对任何一个表
y,空表与其拼接得到的表是y本身 - 任何表
u,v,y,z,(cons u v)与y拼接得到(cons u z)的条件是 v与y的拼接得到z
append 的过程定义和上述两条规则都可以回答下面问题:
- 找出
(a b)和(c d)的append
这两条规则还可以回答(但 append 过程不行):
- 找出一个表
y使(a b)与它的拼接得到(a b c d) - 找出所有拼接起来将得到
(a b c d)的表x和y
在逻辑式程序语言里,可以写出与上面两条规则直接对应的表达式,求值器可以基于它得到上面各问题的解。但各种逻辑语言(包括本小节介绍的)都有缺陷,简单提供“做什么” 知识 有时会使求值器陷入无穷循环,或产生了不是用户希望的行为,这个领域最新的方向是 constraint programming 。
查询系统
本系统所使用的语言为查询语言,该语言的三要素分别是:
-
基本元素,简单查询
(job?persion(computerprogrammer))
-
组合手段,复合查询
(and (job?persion(computerprogrammer)) (address?persion ?where))
-
抽象手段,规则
(rule⟨conclusion⟩ ⟨body⟩) (rule(lives-near?persion-1 ?persion-2) (and(address?persion-1(?town. ?rest-1)) (address?persion-2(?town. ?rest-2)) (not(same?persion-1 ?persion-2))))
可以认为一条规则表示了很大(甚至无穷大)的一集断言,其元素是 由 <conclusion> 求出的所有满足 <body> 的赋值。对简单查询,如果其中变量的某个赋值满足某查询模式,那么用这个赋值实例化模式得到的断言一定在数据库里但满足规则的断言不一定实际存在在数据库里(推导出的事实)。
将逻辑看作程序
规则可看作逻辑蕴涵式:若对所有模式变量的赋值能满足一条规则的体, 则它就满足其结论。可认为查询语言就是基于规则做逻辑推理。还是用 append 为例:
(rule(append-to-form()?y ?y)) (rule(append-to-form(?u. ?v)?y(?u. ?z)) (append-to-form?v ?y ?z))
有了上面的规则,可以做许多查询
;;; Query input: (append-to-form(ab)(cd)?z) ;;; Query results: (append-to-form(ab)(cd)(ab c d)) ;;; Query input: (append-to-form(ab)?y(ab c d)) ;;; Query results: (append-to-form(ab)(cd)(ab c d)) ;;; Query input: (append-to-form?x ?y(ab c d)) ;;; Query results: (append-to-form()(ab c d)(ab c d)) (append-to-form(a)(bc d)(ab c d)) (append-to-form(ab)(cd)(ab c d)) (append-to-form(ab c)(d)(ab c d)) (append-to-form(ab c d)()(ab c d))
这些例子展示了不同方向的计算,正是前面提出希望解决的问题。
查询系统原理
查询系统的组织围绕着两个核心操作:
-
模式匹配(pattern match),操作实现简单查询和复合查询 -
合一(unification),是模式匹配的推广,用于实现规则
逻辑程序设计和数理逻辑
查询语言的组合符对应于常用逻辑连接词,查询操作看起来也具有逻辑 可靠性(例如,and 查询要经过两个子成分处理等)但这种对应关系并不严格,因为查询语言的基础是求值器,其中隐含着控制结构和控制流程,是采用过程的方式解释逻辑语句。
这种隐含的控制结构我们有可能利用,例如,要找程序员的上司,下面两种写法都行:
(and(job?x(computerprogrammer)) (supervisor?x ?y)) (and(supervisor?x ?y) (job?x(computerprogrammer)))
如果公司里的有关上司关系的事实比有关程序员的事实更多,第一种写法的查询效率更高。
逻辑程序设计的目标是开发一种技术,把计算问题分为“要计算什么”和 “怎样计算”两个相互独立的子问题,方法是:
- 找出逻辑语言的一个子集,其
- 功能足够强,足以描述人们想考虑的某类计算
- 又不过分的强,有可能为它定义一种过程式的解释
- 实现一个求值器(解释器),执行对用这种逻辑子集写出的规则和 断言的解释(实现其语义,形式上是做推理)
上面提出的两方面性质保证了逻辑程序设计语言程序的有效性。
本小节的查询语言是这种想法的一个具体实施:
- 查询语言是数理逻辑的一个可以过程式解释的子集
- 一个断言描述一个简单事实
- 一条规则表示一个蕴涵,能使规则体成立的情况都使结论成立
- 规则有自然的过程式解释:要得到其结论,只需确定其体成立
not 问题
(and(supervisor?x ?y) (not(job?x(computerprogrammer)))) (and(not(job?x(computerprogrammer))) (supervisor?x ?y))
这两个查询会得到不同结果(与逻辑里的情况不同):
- 第一个查询找出所有与
(supervisor ?x ?y)匹配的条目,从得到的框架中删去 ?x 满足(job ?x (computer programmer))的框架 - 第二个查询从初始框架流(只包含一个空框架)开始检查能否扩展 出与
(job ?x (computer programmer))匹配的框架。显然空框架可扩展,not 删除流中的空框架得到空流,查询最后返回空流
逻辑程序语言里的 not 反映的是一种“封闭世界假说”,认为所有知识都包含在数据库里,凡是没有的东西其 not 都成立。这显然不符合形式化的数理逻辑,也不符合人们的直观推理。
查询语言的完整代码,可以参考 这里 .
总结
首先恭喜我“完成”第四章,算算大概用了4个月,太多不定因素了,不过还好自己找到了当初的感觉,坚持了下来。
这一章的内容很多,毕竟是设计一门语言,而且还介绍了两种大变种,把书上的代码调通就要花好久,不过也确实开了眼界,通过最基本的eval、apply 循环扩展出了 amb 非确定性求值器与逻辑语言求值器,其实这章的难度并不大,只是涉及的内容广而已。
通过看完这章,发现了很多本质性的东西,像 Node.js 里面的 callback、Python 里面的 generator 不都是 continuation 的糖衣嘛,JIT 也不过尔尔,这章更偏向的是元编程领域,通过 DSL 来减轻业务代码的逻辑,想象如果语言本身就支持分布式事务,程序员要少写多少代码呢。











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

