《每周一点canvas动画》——速度与加速度

在上一节中我们介绍了三角函数的应用，通过三角函数我们让小球实现了 平滑运动 ， 线性运动 ， 圆周运动 等，那么在这一节中呢！我们继续介绍 速度 与 加速度 。这一节的内容也比较简单，不会有太多很难的数学公式，你只需要理解简单的物理概念即可。本节共分为两个部分，在上一节中我们主要介绍：

1. 速度与速率

2. 任意方向的速度

3. 鼠标跟随(运用实例)

4. 扩展

1.速度与速率

速度表征物体运动的快慢。在讲解速度与速率的概念之前，我们需要了解两个数学上的概念： 矢量与标量

ok!忘记上面的定义吧！尽管我们平时在说话时很少区分速度和速率(当然，万一你是学霸呢)到底有怎样的区别。但，实实在在的是在我们的程序中基本上用到的都是 速度 的概念。所以，你只需要记住我们用的这个变量既有数值大小也有方向，就行了。示意图如下：

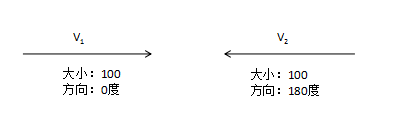
在上图中我们定义了两个速度v1和v2，它们都有相同的大小，但是方向却不相同。简单的介绍完速度的概念，那么怎样把它运用在我们的动画中呢？假如现在我要让我的小球沿着X轴的方向运动，具体代码如下：

 <canvas id="canvas" width="500" height="500" style="background:#000;">         your browser not support canvas     </canvas>     <script src="../js/ball.js"></script>     <script src="../js/utils.js"></script>     <script>         window.onload = function(){             var canvas = document.getElementById('canvas');             var context = canvas.getContext('2d');                          var ball = new Ball();                 ball.x = canvas.width/4;                 ball.y = canvas.height/4;              var vx = 1; //定义速度                          //动画循环中             (function drawFrame(){                 window.requestAnimationFrame(drawFrame, canvas);                 context.clearRect(0, 0, canvas.width, canvas.height);                                  ball.x += vx; // 在每一帧中都让小球的位置加上速度                                  ball.draw(context);             }());         }     </script>

首先，我们引入我们的工具文件 utils.js 和 ball.js 这两个文件如果你还没有添加到你的js目录中，可以去前两节的代码中找，工具文件 utils.js 在用户交互这一章， ball.js 在三角函数(2)这一章。我还是劝你把前面的文件添加到自己的项目目录中，以方便使用。后面我会考虑把源码放在github上。现在，就暂时麻烦一下各位小主自己添加一下了！

好了，言归正传，在上面的代码中，我们定义了一个速度vx，并在动画循环中让球的x轴坐标每一帧都加上速度值！ok,小球沿着x轴正方向的运动，动画完成！

那么，如果你想要让小球沿着Y轴的正方向做运动呢？so easy!定义一个速度vy,然后，让小球的纵坐标值每帧都加上速度值不就行了。

var vy = 1; //定义速度 ....     ball.y += vy // 在每一帧中都让小球的位置加上速度

看看现在小球是不是沿着Y轴在运动。

那么，如果我们同时在X轴和Y轴方向上定义了速度，并且在X和Y方向都加上速度，会是什么效果呢？

var vx = 1; var vy = 1; ...     ball.x += vx;     ball.y += vy; 

我们可以看到小球既不沿着x轴也不沿着y轴运动，而是沿着一个45度角的方向在做运动。这里就引出了我们的下一部分——任意方向的速度。

2.任意方向的速度

通过上面的代码演示，我们知道，当同时在一个物体的x轴和y轴上定义速度，那么物体的运动方向是这两个速度方向的 合方向 ，即满足矢量的叠加，大小满足勾股定理。

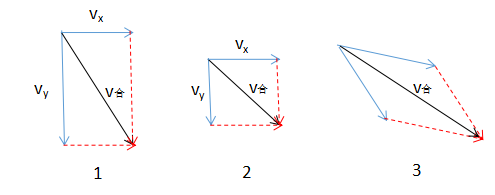
在上图中，图1和图2,我们分别在X轴和Y轴上定义了速度Vx和Vy,那么他们的合速度满足平行四边形规则，即图中的 V合 ，我们可以看到合速度的大小满足勾股定理，而它的方向因为在坐标轴上的分量不相同，所以合速度方向也不相同。至于第三附图，其实跟前两幅图没什么区别，只是它的两个速度方向并不是沿着坐标轴。这与物理中力的合成与分解是一样样的，在这我就不废话了。

既然，我们知道了可以通过控制沿坐标轴方向的速度来改变物体的运动方向和运行的快慢。想想在三角函数那一章，如果我们想要让小球做一个圆周运动，用这种方法可行吗？

答案是绝对可以实现的！但是，考虑一下在圆周运动中物体的运动速度方向是不是时刻都在发生变化啊，那如果你想要得到一个完美的圆周运动，就需要时刻改变X轴和Y轴的坐标值。我的天,这是多么大的工作量。所以，在那一章中我推到了从 圆的直角坐标表达式 到 圆的极坐标表达式 ，为的就是找到方便控制的变量。

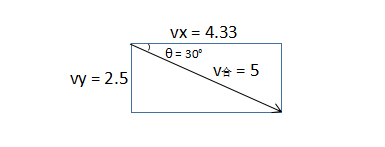
那么现在，我们想让小球按照我们指定的方向任意运动，该怎么办呢？答案是三角函数啦。。。，试想现在导演说：小球，你以每秒5米的速度，30度角方向运动。那么从中我们得到的信息量是，小球的合速度是5，方向是30度。那么把它分解到坐标轴上就是 vy = 2.5 , vx = 4.33 。

那么具体到我们的代码里该如何应用呢？

... var speed = 5; var angle = 30; (function drawFrame(){                window.requestAnimationFrame(drawFrame, canvas);                context.clearRect(0, 0, canvas.width, canvas.height);                                //将速度分解到X轴和Y轴，注意这里用的是弧度制，要乘上Math.PI/180                var vx = Math.cos(angles*Math.PI/180)*speed;                var vy = Math.sin(angles*Math.PI/180)*speed;                                //坐标位置每一帧都加上速度                ball.x += vx;                ball.y += vy;                ball.draw(context);            }())

ok!在代码中我们直接定义了物体的运行速度，和运行的方向。然后在动画循环中通过三角函数动态的去计算每一帧在x轴和Y轴上应该移动的距离。这样是不是方便很多，也很好控制呢。

3.鼠标跟随

了解了上面的知识，现在我们来模拟一个很炫酷的动画。我叫它 鼠标跟随 ，它实现的效果就是让物体跟着鼠标移动，每当你改变鼠标的位置，物体就会改变它的运动方向，并朝着鼠标的方向移动作匀速移动。还记得我们在三角函数(1)结尾的运用实例吗？在那个实例中我们做了一个跟随鼠标旋转的箭头，今天我们做的这个鼠标跟随的效果就是在此基础上，运用本章所学内容的一个改进。

其实这里能放个GIF图片是最好的，但一直苦于找不到好的制作软件，就先上两图，让大家YY了。有什么好用的做GIF的软件麻烦推荐一下啦。具体代码如下：

<canvas id="canvas" style="background:#000;" width="500" height="500">        you browser not support canvas    </canvas>    <script src="../js/arrow.js"></script>    <script src="../js/utils.js"></script>    <script>        window.onload = function(){            var canvas = document.getElementById("canvas");            var context = canvas.getContext("2d");            //获取鼠标相对canvas的位置            var mouse = utils.captureMouse(canvas);                        var arrow = new Arrow();            arrow.x = canvas.width/2;            arrow.y = canvas.height/2;                        var angle = 0, speed = 2; //定义速度和方向                        (function drawFrame(){                window.requestAnimationFrame(drawFrame, canvas);                context.clearRect(0,0,canvas.width,canvas.height);                                //这点看不懂的话，就去复习一下吧，我们要用它来计算角度                var dx = mouse.x - arrow.x;                 var dy = mouse.y - arrow.y;                                 //得到角度值                angle = Math.atan2(dy, dx);                                //箭头旋转                arrow.rotation = angle;//angle默认为弧度                                //将速度分解                var vx = Math.cos(angle)*speed;                var vy = Math.sin(angle)*speed;                                //移动                arrow.x += vx;                arrow.y += vy;                //绘制                arrow.draw(context);            }());        }     </script>

这里我们首先初始化好速度和角度，然后将鼠标的坐标值减去箭头的坐标位置，得到dx,dy, 然后运用Math.atan2()得到角度值(通过此方法得到的是弧度)，最后运用三角函数将速度分解到x和y方向。简单吧，但实现的效果确是刚刚的。 arrow.js 文件在三角函数(1)中，你最好还是添加到你的js文件中吧！

4.扩展

前面我们介绍了怎样通过三角函数来实现任意方向的速度。那么还有其他的方法改变物体的运动方向吗，在这部分中我们介绍一个扩展方法，他运用的是canvas的rotation()方法，具体代码如下：

window.onload = function() {            var canvas = document.getElementById("canvas");            var context = canvas.getContext("2d");                        var arrow = new Arrow();            arrow.x = canvas.width/2;            arrow.y = canvas.height/2;                        var vr = 30, speed = 2;                        (function drawFrame(){                window.requestAnimationFrame(drawFrame, canvas);                context.clearRect(0,0,canvas.width,canvas.height);                                //通过rotation来改变角度值                arrow.rotation = vr*Math.PI/180;                //分解                arrow.x += Math.cos(arrow.rotation)*speed;                arrow.y += Math.sin(arrow.rotation)*speed;                                arrow.draw(context);            }())        } 

这里我们通过改变箭头的rotation属性来定义方向，然后其他的都是一样的将速度分解到x方向和y方向，坐标位置改变等。好了，这一节的内容到这也就全部结束了，我会在每一章结束时，对这章的重要公式最一下总结！下一节加速度敬请期待！当然如果有好的GIF制作软件麻烦推荐一下。