转载

最小生成树 prim 和 Kruskal 详细学习笔记

定义

最小生成树是一副连通加权无向图中一棵权值最小的生成树。

最小生成树其实是 最小权重生成树 的简称。

可能翻译为 最小权重生成树 更容易理解一些。意思就是说在图中的每条边都加上权值，所谓权值是一种抽象的含义。可以指代一切可以量化的东西。比如说修路的费用，路程等等。然后在图中找到这样一棵树，边的权值加起来最小。并且既然是棵树，必须满足的要求是无环.

一般用两种贪心算法来找到最小生成树，分别是 prim 和 Kruskal

`Kruskal`

Kruskal 算法，我觉得比较容易理解，实现也比较简单。

新建图G
把图G中所有的边按照权值从小到大排序。(一般使用优先队列)
取出最小的边
如果这条边连接的两个节点于图G中不在同一个连通分量中，则添加这条边到图G中.(使用并查集)
重复3，直至图G中所有的节点都在同一个连通分量中

实现代码

public class KruskalMST {

    private Queue<Edge> mst = new Queue<>();
    private double weight;

    public KruskalMST(EdgeWeightedGraph g){
        MinPQ<Edge> minPQ = new MinPQ<>();
        for (Edge edge:g.edges()){
            minPQ.insert(edge);
        }
        UF uf =new UF(minPQ.size());
        while (!minPQ.isEmpty()){
            Edge edge = minPQ.delMin();
            int v = edge.either();
            int w = edge.other(v);
            if(!uf.connected(v,w)){
                uf.union(v,w);
                mst.enqueue(edge);
                //weight+=edge.weight();
            }
        }
    }
}

性能分析

Kruskal 算法基本上取决于优先队列的选择，以及并查集的实现。

比较优的算法效率为 O(ElogE) E为图中的边数.

对优先队列和并查集不了解的同学可以看看我这两篇文章，查找算法之顺序、二分、二叉搜索树、红黑树和并查集

Prim

Prim 算法，简单的说就是 从一个点开始不断让树长大的过程,并且保持权值最小 。

生成图G
从s点开始
把与s点相连的边都加入 edgeTo[] ,并且保存到这些点的距离 distTo[] ,且插入到优先队列
出队一个点
查找与这个点相连的点，若权值比 distTo[] 中保存的值小则进更新，同时更新 distTo[] 和优先队列.
重复4

如下图

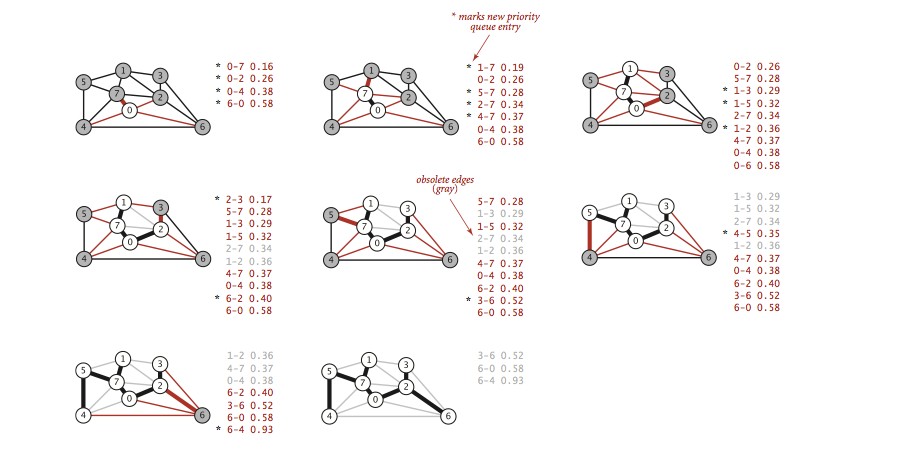
最小生成树 prim 和 Kruskal 详细学习笔记

实现代码

private Edge[] edgeTo;        // edgeTo[v] = shortest edge from tree vertex to non-tree vertex
    private double[] distTo;      // distTo[v] = weight of shortest such edge
    private boolean[] marked;     // marked[v] = true if v on tree, false otherwise
    private IndexMinPQ<Double> pq;

    public PrimMST(EdgeWeightedGraph G){
        edgeTo = new Edge[G.V()];
        distTo = new double[G.V()];
        marked = new boolean[G.V()];
        pq = new IndexMinPQ<Double>(G.V());
        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;

        for (int v = 0; v < G.V(); v++)      // run from each vertex to find
            if (!marked[v]) prim(G, v);      // minimum spanning forest
    }

    private void prim(EdgeWeightedGraph g, int s) {
        distTo[s]=0;
        pq.insert(s,distTo[s]);
        while (!pq.isEmpty()){
            grow(g,pq.delMin());
        }
    }

    private void grow(EdgeWeightedGraph g, int v) {
        marked[v]=true;
        for (Edge e :g.adj(v)){
            int w = e.other(v);
            if(marked[w])   continue;
            if(distTo[w]>e.weight()){
                distTo[w]=e.weight();
                edgeTo[w] = e;
                if(pq.contains(w))
                    pq.decreaseKey(w,distTo[w]);
                else
                    pq.insert(w,distTo[w]);
            }
        }

    }