强化学习系列之四:模型无关的策略学习
模型无关的策略学习,是在不知道马尔科夫决策过程的情况下学习到最优策略。模型无关的策略学习主要有三种算法: MC Control, SARSA 和 Q learning。
文章目录
1. 一些前置话题
在模型相关强化学习中,我们的工作是找到最优策略的状态价值 
。但是在模型无关的环境下,这个做法却行不通。如果我们在模型无关环境下找最优策略的状态价值  ,在预测时,对状态
,在预测时,对状态  最优策略如下所示。
最优策略如下所示。
/begin{eqnarray}
/pi(s,a) =
/left/{/begin{matrix}
1 & a = argmax_{a}R_{s,a}+/gamma /sum_{s' /in S}T_{s,a}^{s'}v(s') //
0 & a /neq argmax_{a}R_{s,a}+/gamma /sum_{s' /in S}T_{s,a}^{s'}v(s')
/end{matrix}/right. /nonumber
/end{eqnarray}
同学们看到 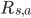 和
和 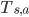 了没?在模型无关的设定下,我们不知道这两个值。也许有同学说可以在预测时探索环境得到
了没?在模型无关的设定下,我们不知道这两个值。也许有同学说可以在预测时探索环境得到 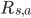 和
和 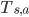 。但是实际问题中,探索会破坏当前状态。比如机器人行走任务中,为了探索机器人需要做出一个动作,这个动作使得机器人状态发生变化。这时候为原来状态选择最优动作已经没有意义了。解决办法是把工作对象换成状态-动作价值
。但是实际问题中,探索会破坏当前状态。比如机器人行走任务中,为了探索机器人需要做出一个动作,这个动作使得机器人状态发生变化。这时候为原来状态选择最优动作已经没有意义了。解决办法是把工作对象换成状态-动作价值 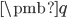 。获得最优策略的状态-动作价值
。获得最优策略的状态-动作价值 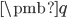 之后,对于状态
之后,对于状态 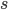 最优策略如下所示。
最优策略如下所示。
/begin{eqnarray}
/pi(s,a) =
/left/{/begin{matrix}
1 & a = argmax_{a}q(s,a) //
0 & a /neq argmax_{a}q(s,a)
/end{matrix}/right. /nonumber
/end{eqnarray}
另一个话题关于贪婪策略。最优策略是贪婪策略,这个不用怀疑。但对于学习来说,贪婪策略不一定是最好的。举个栗子,状态集合为 {A, B, C, D}, 其中 A 是起始状态而 D 是终止状态。A->B 奖励为1 而 C->D 奖励为100,其他奖励为0。从起始状态 A, 贪婪策略会一直选择进入 B,而不探索 C 从而获得更高奖励。为了鼓励探索,我们用了另一种 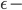
贪婪策略,其公式如下。
/begin{eqnarray}
/pi_{/epsilon-greedy}(s,a) =
/left/{/begin{matrix}
1-/epsilon & a = argmax_{a}q(s,a)//
/frac{/epsilon}{|A|} & a /neq argmax_{a}q(s,a)
/end{matrix}/right. /nonumber
/end{eqnarray}
2. MC Control
一听到 Monte Carlo Control (MC Control) 这个名字,我们就知道,这个算法生成样本然后根据样本计算状态-动作价值。对于每一个状态-动作对,我们都要维持他们的价值 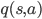
和被访问次数 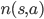 。让系统采样一个状态-动作-奖励的系列,然后对于每个状态-动作更新价值和次数。
。让系统采样一个状态-动作-奖励的系列,然后对于每个状态-动作更新价值和次数。
/begin{eqnarray}
q(s,a) &=& /frac{q(s,a) * n(s,a) + g}{n(s,a)+1} /nonumber //
n(s,a) &=& n(s,a) + 1 /nonumber
/end{eqnarray}
其中
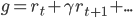
是预期衰减奖励之和。MC Control 算法的代码如下。
def mc(num_iter1, epsilon): n = dict(); for s in states: for a in actions: qfunc["%d_%s"%(s,a)] = 0.0 n["%d_%s"%(s,a)] = 0.001 //平滑 for iter1 in xrange(num_iter1): s_sample = [] a_sample = [] r_sample = [] s = states[int(random.random() * len(states))] t = False while False == t: a = epsilon_greedy(s, epsilon) t, s1, r = grid.transform(s,a) s_sample.append(s) r_sample.append(r) a_sample.append(a) s = s1 g = 0.0 for i in xrange(len(s_sample)-1, -1, -1): g *= gamma g += r_sample[i]; for i in xrange(len(s_sample)): key = "%d_%s"%(s_sample[i], a_sample[i]) n[key] += 1.0; qfunc[key] = (qfunc[key] * (n[key]-1) + g) / n[key] g -= r_sample[i]; g /= gamma;
在 MC Control 算法中,状态-动作价值会收敛到 
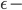
贪婪策略算出了状态-动作价值
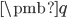
。如果在预测时采用贪婪策略,系统很有可能是遵循最优策略。
还是拿机器人找金币当例子。机器人从任意一个状态出发寻找金币,找到金币则获得奖励 1,碰到海盗则损失 1。找到金币或者碰到海盗,机器人都停止。衰减因子 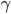
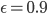 贪婪策略的
贪婪策略的 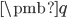
(1 状态标示了所有的 q 值,其他状态只标示了最大的 q 值,其中 ),0.9 是很大的
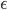
表示策略有很大的随机性。在这个状态-动作价值采用贪婪策略,策略动作和右边最优策略采取的动作完全一致。
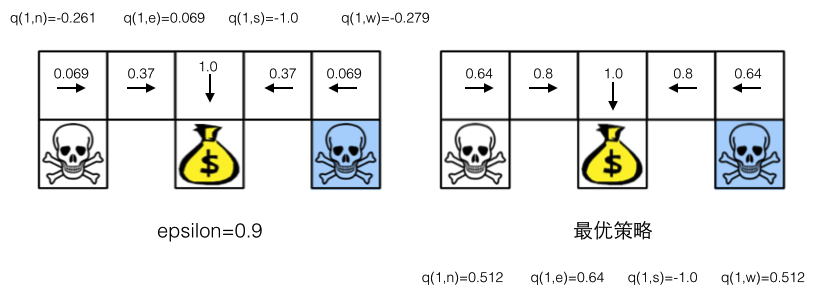
不知道这个论断理论上是不是成立的?如果有哪位大牛了解,期待您的指导。
3. SARSA
State Action Reward State Action (SARSA) 算法其实是状态-动作价值版本的时差学习 (Temporal Difference, TD) 算法。SARSA 利用马尔科夫性质,只利用了下一步信息。SARSA 让系统按照策略指引进行探索,在探索每一步都进行状态价值的更新,更新公式如下所示。
/begin{eqnarray}
q(s,a) = q(s,a) + /alpha (r + /gamma q(s',a') - q(s,a))
/end{eqnarray}
s 为当前状态,a 是当前采取的动作,s' 为下一步状态,a' 是下一个状态采取的动作,r 是系统获得的奖励,

是学习率,
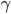
是衰减因子。SARSA 的代码如下。
def sarsa(num_iter1, alpha, epsilon): for s in states: for a in actions: key = "%d_%s"%(s,a) qfunc[key] = 0.0 for iter1 in xrange(num_iter1): s = states[int(random.random() * len(states))] a = actions[int(random.random() * len(actions))] t = False while False == t: key = "%d_%s"%(s,a) t,s1,r = grid.transform(s,a) a1 = epsilon_greedy(s1, epsilon) key1 = "%d_%s"%(s1,a1) qfunc[key] = qfunc[key] + alpha * ( / r + gamma * qfunc[key1] - qfunc[key]) s = s1 a = a1
SARSA 收敛到哪里呢?和 MC Control 算法一样,SARSA 的状态-动作价值也收敛到 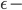
贪婪策略的状态-动作价值上。
4. Q Learning
Q Learning 的算法框架和 SARSA 类似。Q Learning 也是让系统按照策略指引进行探索,在探索每一步都进行状态价值的更新。关键在于 Q Learning 和 SARSA 的更新公式不一样,Q Learning 的更新公式如下。
/begin{eqnarray}
q(s,a) = q(s,a) + /alpha /{r + argmax_{a'}/{/gamma q(s',a')/} - q(s,a)/}
/end{eqnarray}
Q Learning 的代码如下。
def qlearning(num_iter1, alpha, epsilon): for s in states: for a in actions: key = "%d_%s"%(s,a) qfunc[key] = 0.0 for iter1 in xrange(num_iter1): s = states[int(random.random() * len(states))] a = actions[int(random.random() * len(actions))] t = False while False == t: key = "%d_%s"%(s,a) t,s1,r = grid.transform(s,a) key1 = "" qmax = -1.0 for a1 in actions: if qmax < qfunc["%d_%s"%(s1,a1)]: qmax = qfunc["%d_%s"%(s1,a1)] key1 = "%d_%s"%(s1,a1) qfunc[key] = qfunc[key] + alpha * ( / r + gamma * qfunc[key1] - qfunc[key]) s = s1 a = epsilon_greedy(s1, epsilon)
Q Learning 的收敛性是很好玩的。Q Learning 与 MC Control 和 SARSA 一样采用了 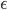
-贪婪策略,但 Q Learning 的状态-动作价值却能收敛到最优策略的状态-动作价值。
5. 做点实验
实验室还是以机器人找金币为场景。机器人从任意一个状态出发寻找金币,找到金币则获得奖励 1,碰到海盗则损失 1。找到金币或者碰到海盗,机器人都停止。衰减因子 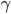
设为 0.8。
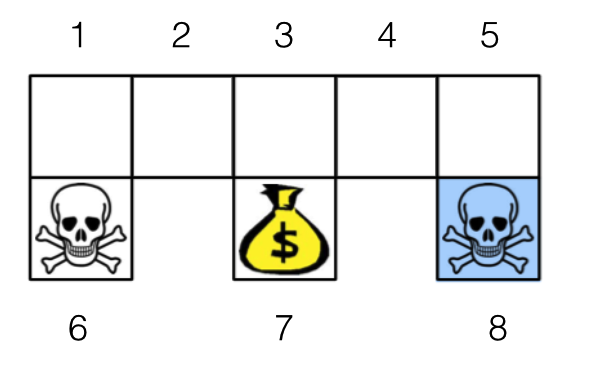
我们将算法计算得到的状态-动作价值和最优策略的状态-动作价值之间的平方差,作为评价指标,其计算公式如下。
/begin{eqnarray}
square-error = /sum_{s /in S, a /in A} /{q(s,a) - q^{*}(s,a)/}^2
/end{eqnarray}
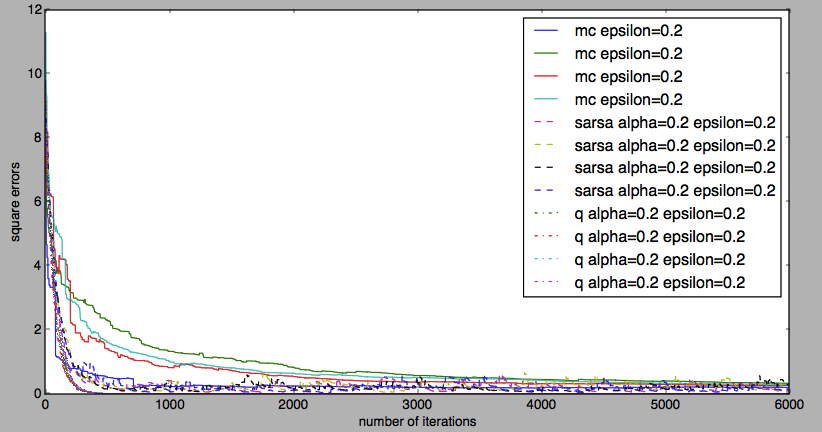
其中
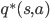
是最优策略的状态-动作价值。
5.1. 算法稳定性
MC Control、 SARSA 和 Q Learning 在算法运行过程中,都有随机因素。我们会关心每次运行的效果是类似的还是差别很大,也就是算法的稳定性。从下图我们可以看到,MC Control 是最不稳定的算法。平方误差下降阶段,SARSA 的稳定性很好,但收敛之后 SARSA 会上下抖动。 Q Learning 拥有良好的稳定性。
5.2.  贪婪策略的影响
贪婪策略的影响
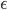 最大为 1 的时候,MC Control 和 SARSA 的平方误差很大,Q Learning 能够让平方误差降到 0。其实这个时候
最大为 1 的时候,MC Control 和 SARSA 的平方误差很大,Q Learning 能够让平方误差降到 0。其实这个时候 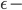
贪婪策略相当于随机策略。MC Control 和 SARSA 的状态-动作价值收敛到了随机策略的状态-动作价值,因此保持一个比较大的值。Q Learning 依然能够收敛到最优策略的状态-动作价值,因此能降到 0。随着
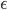
的下降,MC Control 和 SARSA 收敛之后的平方误差会降低,Q Learning 则一如既往地降到 0。
这个实验表明 Q learning 能从其他策略探索经验中学习。我们称能够从其他策略学习到最优策略的算法为离策略 (off-policy) 算法,反之为在策略 (on-policy) 算法。MC Control 和 SARSA 是在策略的,Q Learning 是离策略的。
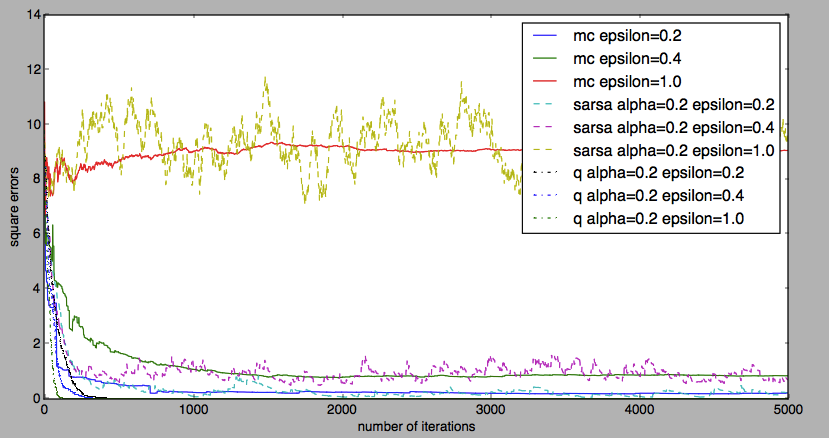
还有一点就是, 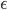
越大, SARSA 收敛之后抖动就越厉害。
5.3. 不同算法的效果对比
全面考察这三种算法,在机器人找金币这个场景上,Q Learning 要好于 SARSA,SARSA 要好于 MC Control。

6. 总结
本文介绍了模型无关的策略学习。模型无关的策略学习主要有三种算法: Monte Carlo Control, Sarsa 和 Q learning。本文代码可以在 Github 上找到,欢迎有兴趣的同学帮我挑挑毛病。强化学习系列的下一篇文章将介绍基于梯度的强化学习。
文章结尾欢迎关注我的公众号 AlgorithmDog,每周日的更新就会有提醒哦~

强化学习系列系列文章
- 强化学习系列之一:马尔科夫决策过程
- 强化学习系列之二:模型相关的强化学习
- 强化学习系列之三:模型无关的策略评价
- 强化学习系列之四:模型无关的策略学习











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

