转载

Find Convex Hull with Graham Scan & Swift

凸包(Convex hull) 是一个数学上的概念，在二维平面上可以想象成用一个橡皮筋套住一堆钉在平面上的钉子。本文讲述如何使用 Swift 实现 Graham scan 算法来寻找二维平面点集上的凸包。工程源码 Github： https://github.com/yulingtianxia/Algorithm-Experiment

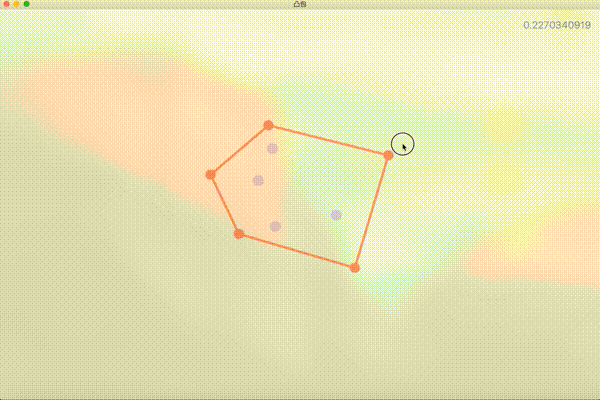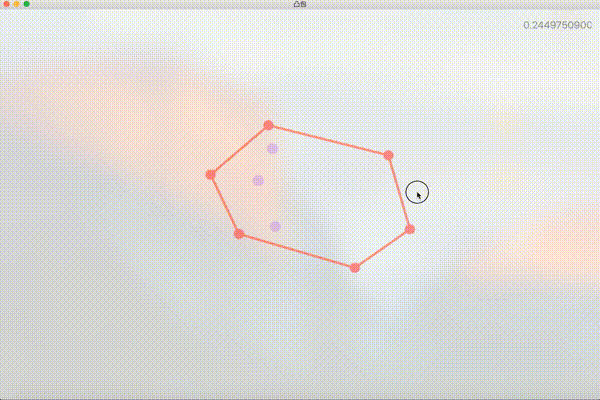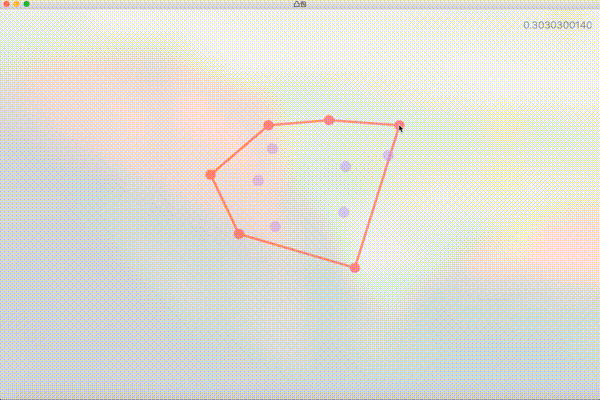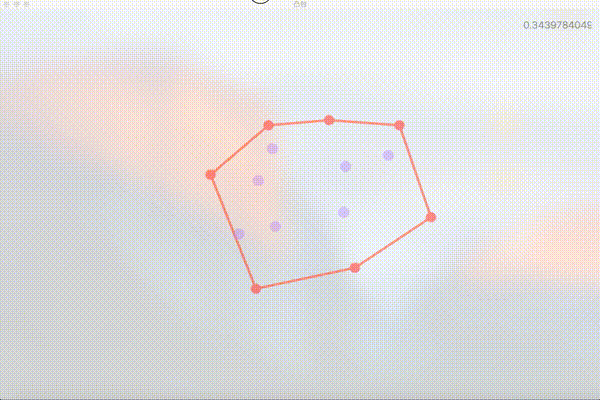
简单粗暴的想法

直观上去看可以理解为『找出最外围的点』，进而把问题转化为『剔除凸多边形内部的点』，进而简化为『剔除任意三角形内的点』。PS： 三角形 指的是由点集内任意三个不相同的点构成的三角形，以下不再赘述定义，直接以 三角形 代指。

下面需要做的是遍历所有三角形的排列组合，找出三角形上或内部的点，并剔除，因为它肯定不是凸包的顶点。

如何判断一个点 P 是否在三角形 ABC 里面呢？

很简单！如果点 P 在三角形 ABC 内，点 A 和 P 肯定在直线 BC 的同一侧，点 B 和 P 也肯定在直线 AC 同一侧，点 C 和 P 必定也在直线 AB 同一侧！

果然够简单粗暴！

假设直线 BC 方程为 ax + by + c = 0 ,如果点 P(Xp,Yp) 在直线 BC 上，则有 a·Xp + b·Yp + c = 0 ；如果点 P(Xp,Yp) 与点 A(Xa,Ya) 在直线 BC 同一侧，则有 (a·Xp + b·Yp + c)(a·Xa + b·Ya + c) > 0 。为了不被吐槽拿初中数学忽悠人，还是快速上代码吧：

func calculatePoint(pointP:CGPoint,onLine line:(pointA:CGPoint,pointB:CGPoint)) -> CGFloat {
    return (pointP.y - line.pointA.y) * (line.pointB.x - line.pointA.x) - (line.pointB.y - line.pointA.y) * (pointP.x - line.pointA.x)
}

func checkPoint(P:CGPoint,inTriangle triangle:(A:CGPoint,B:CGPoint,C:CGPoint)) -> Bool {
    var Pp = calculatePoint(P, onLine: (triangle.A,triangle.B))
    let AB = Pp == 0||Pp * calculatePoint(triangle.C, onLine: (triangle.A,triangle.B)) > 0
    if !AB{
        return AB
    }
    Pp = calculatePoint(P, onLine: (triangle.A,triangle.C))
    let AC = Pp == 0||Pp * calculatePoint(triangle.B, onLine: (triangle.A,triangle.C)) > 0
    if !AC{
        return AC
    }
    Pp = calculatePoint(P, onLine: (triangle.C,triangle.B))
    let BC = Pp == 0||Pp * calculatePoint(triangle.A, onLine: (triangle.C,triangle.B)) > 0

    return AB && AC && BC
}

calculatePoint: onLine: 函数的作用是将点坐标代入直线方程式并返回计算结果； checkPoint: inTriangle: 函数的作用是判断某点是否在三角形上或内部。

在开始暴力遍历所有的三角形组合并剔除不符合要求的点之前，我想再声明一个命题：『X 轴和 Y 轴的极值点肯定是凸包顶点』。也就是说如果一个点的 X 坐标最大，那么它肯定是凸包顶点。这个命题像是废话，用反证法其实也很容易证明：假如 Y 值最大的点 P 不是凸包顶点，那么必然处于某个三角形 ABC 内，并且 ABC 三个点的 Y 值都比 P 小，假设 A 点为三角形 ABC 中 Y 值最小的点，则 P 点和 A 点必然处于直线 BC 两侧，矛盾。命题得证。

PS：这里注意我们想要的结果仅仅是 凸包顶点 ，有些点可能位于两个相邻的凸包顶点连线上，这样的点只能算作 凸包上的点 ，它们与 凸包内的点 一样需要被剔除。

我们最终输出的结果希望是逆时针顺序输出的，比如下图中的凸包顶点输出顺序应为： A,B,C,D,E,F,G,H ，其中 A 点和 D 点分别为 X 最小的点和 X 最大的点。

Find Convex Hull with Graham Scan & Swift

有两种方案可以按照逆时针顺序输出结果：

以 A 点为中心，向量 DA 方向做射线逆时针扫描，按照扫描到点的顺序输出即可，直至 360° 扫描完毕。
将直线 AD 上方的点集 Su 按照 X 值从大到小排列，下方的点集 Sd 按照 X 值从小到大排列，最后输出顺序为： A，Sd，D，Su

很明显，第二种方案计算量小并且实现简单。

但受到方案 1 的启发，我们可以将暴力遍历的时间复杂度减少一层。将 A 点与其他凸包顶点连上虚线：

Find Convex Hull with Graham Scan & Swift

也就是说可以把 A 点作为公共点来遍历三角形。因为 A 点肯定不会被剔除，并且上图中以 A 点为公共点的三角形已经覆盖了所有的点，不用担心会有遗漏。于是三角形的一个顶点已经确定下来了，只需遍历生成另两个顶点和一个需要判定是否在三角形内的点，四层循环嵌套降为三层！

献上核心算法的 Swift 代码：

func generateConvexHull(inout points:[PointView]){
   for point in points {
       point.isConvexHullNode = true
   }
   
   if points.count <= 3 {
       return
   }
   
   var minXPoint = points[0]
   var maxXPoint = points[0]
   for point in points {
       minXPoint = point.position.x < minXPoint.position.x ? point : minXPoint
       maxXPoint = point.position.x > maxXPoint.position.x ? point : maxXPoint
   }
   
   let point1 = minXPoint;
   for point2 in points {
       if !point2.isConvexHullNode || point2 == point1 {
           continue
       }
       for point3 in points {
           if !point3.isConvexHullNode || point3 == point1 || point3 == point2 {
               continue
           }
           for point4 in points {
               if !point4.isConvexHullNode || point4 == point1 || point4 == point2 || point4 == point3 {
                   continue
               }
               if checkPoint(point4.position, inTriangle: (point2.position,point3.position,point1.position)) {
                   point4.isConvexHullNode = false
                   continue
               }
           }
       }
   }
   
   var su = points.filter {
       calculatePoint($0.position, onLine: (minXPoint.position,maxXPoint.position)) > 0
   }
   var sl = points.filter {
       calculatePoint($0.position, onLine: (minXPoint.position,maxXPoint.position)) < 0
   }
   su = su.sort {
       return ($0.position as CGPoint).x > ($1.position as CGPoint).x
   }
   sl = sl.sort {
       return ($0.position as CGPoint).x < ($1.position as CGPoint).x
   }
   var result = [minXPoint]
   result += sl
   result.append(maxXPoint)
   result += su
   points = result
}

这么暴力的算法复杂度也是高的惊人，为 O(N^3) ！想必此时已经有不少已经脱了裤子的同学想问博主为什么要给自己看这些！说好的 Graham scan 算法呢？其实这部分『前戏』很重要，绝不是为了凑篇幅，一些重要概念对后面的正题理解有很大帮助，比如下面要介绍的 PointView 类（卧槽表碧莲啊还来！）

PointView 是算法演示程序中用于绘制和存储二维点坐标信息的类，它不仅存储坐标，还维护了状态 isConvexHullNode ，并根据状态值是否为凸包顶点来改变 UI（红色的点为凸包顶点，紫色为非凸包顶点）。此外 PointView 还需要处理鼠标拖拽事件。这部分比较简单，就不上代码了。

Graham Scan

当沿着凸包逆时针漫游时，你会发现总是在『向左拐』；反之则是『向右拐』。

还记得之前说的以 A 点为中心逆时针扫描所有点的方案吧？将所有除 A 以外的点按照这个扫描顺序进行排列。然后在此基础上遍历并剔除『不向左拐』的点，最后输出的点集正好是按顺序排列好的。

PS:判断 P1P2P3 在 P2 拐弯方向公式： (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x) ，如果其结果为 0 ，这三个点是共线的，如果其结果为正，这三个点是向左拐的，否则，它是向右拐的。

为了方便计算，通常选择 Y 值最小的点作为 A 点（Y 值一样就选最右边的点），其余的点就都落在第一、二象限。

下图来自维基百科，但是漫游方向是 顺时针 的，也就是说要剔除 不向右拐 的点：

Find Convex Hull with Graham Scan & Swift

在 P 为原点的极坐标下按照极角大小构造顺时针排序的数组： [A,B,C,D] ，计算极角的函数实现如下：

func calculatePolarAngle(origin:CGPoint, target:CGPoint) -> Double {
    let trans = (x: target.x - origin.x, y: target.y - origin.y)
    let angle = atan(Double(trans.y) / Double(trans.x))
    switch trans {
    case let (x,y) where x >= 0 && y >= 0:
        return angle
    case let (x,y) where x < 0 && y >= 0:
        return angle + M_PI
    case let (x,y) where x <= 0 && y < 0:
        return angle + M_PI
    case let (x,y) where x > 0 && y < 0:
        return angle + 2 * M_PI
    default:
        return 0
    }
}

接着就是遍历按极角排序好的数组。先将 P 点和 A 点 push 进栈，然后检查 PAB 是否不向右拐，因为在 A 点右拐所以将 B 点 push 进栈，然后继续检查 C 点。可以看出在 C 点处 BCD 向左拐了，于是 C 点被剔除，栈 pop 出 C 。然后检查 ABD 处是否符合要求，结果是符合要求的，于是将 D 点 push 进栈。

也就是说遍历数组时始终判断栈顶元素处拐弯方向是否符合要求：方向符合要求则将当前遍历的点 push 进栈，否则将栈顶元素 pop，并继续判断栈顶元素处拐弯是否符合要求，直到符合要求为止。（如若栈元素个数小于 3 ，则不再 pop）

最后的实现算法 Swift 代码如下（逆时针漫游）

func generateConvexHull(inout points: [PointView]) {
   for point in points {
       point.isConvexHullNode = true
   }
   
   if points.count <= 3 {
       return
   }
   
   var minYPoint = points[0]
   var minIndex = 0
   for (index,point) in points.enumerate() {
       (minIndex,minYPoint) = point.position.y < minYPoint.position.y ? (index,point) : (minIndex,minYPoint)
   }
   points.removeAtIndex(minIndex)
   points.sortInPlace {
       return calculatePolarAngle(minYPoint.position, target: $0.position) < calculatePolarAngle(minYPoint.position, target: $1.position)
   }
   var stack = [minYPoint]
   var restPoints = [PointView]()
   stack.append(points[0])
   
   for point in points[1..<points.count] {
       
       func checkTurnsRight() -> Bool {
           let p1 = stack[stack.count-2].position
           let p2 = stack.last!.position
           let p3 = point.position
           return (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x) <= 0
       }
       
       while checkTurnsRight() {
           stack.last?.isConvexHullNode = false
           restPoints.append(stack.last!)
           stack.removeLast()
           if stack.count < 3 {
               break
           }
       }
       stack.append(point)
   }
   points = stack + restPoints
}

Graham Scan 的时间复杂度是 O(nlogn) ，而且只适用于二维平面。算法导论上也讲到了包裹法（Jarvis步进法）和分治法，时间复杂度都是 O(nlogn) 。我的那个工程里也有分治法的 Swift 实现。如果拓展到多维空间，我觉得使用 Swift 并不是一个很好的实现语言，Matlab 再适合不过了。

后记

博主江郎才尽竟然拿学校的某次算法实验充数尼玛坑爹呢这是！

原文 http://yulingtianxia.com/blog/2016/04/28/Find-Convex-Hull-with-Graham-Scan-Swift/

正文到此结束

所属分类：编程技术

本文标签： UI Swift find REST tar 遍历 App https 空间 git 时间 ACE node 代码 http 源码 GitHub src
版权声明： 本文为互联网转载文章，出处已在文章中说明(部分除外)。如果侵权，请联系本站长删除，谢谢。
本文海报： 生成海报一生成海报二