转载

强化学习系列之五:进入实际问题的关键——价值函数近似

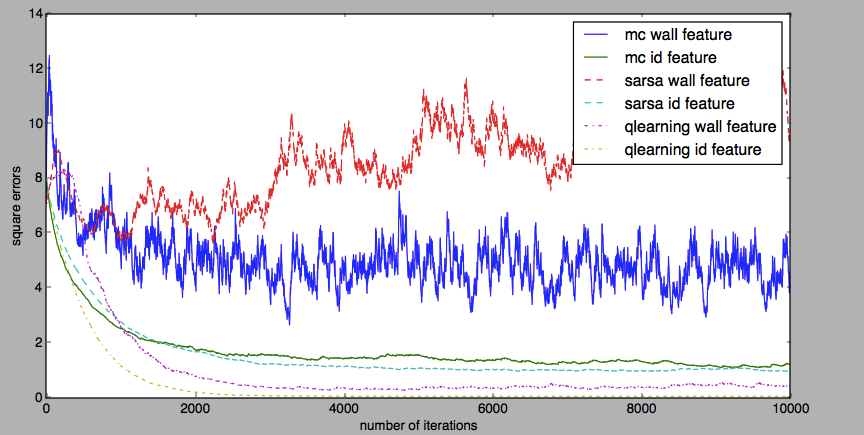
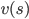
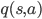目前，我们已经介绍了一些强化学习的算法，但是我们无法在实际问题中运用这些算法。为什么呢？因为算法估算价值函数强化学习系列之五:进入实际问题的关键——价值函数近似

或者

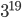，保存这些价值函数意味着保存所有状态。而实际问题中，状态的数目非常巨大，遍历一遍的事情就别想了。比如，围棋的状态总数是强化学习系列之五:进入实际问题的关键——价值函数近似

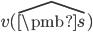
，听说比宇宙的总原子数还多，23333。解决这个问题的方法是抽特征。对于一个状态 s, 我们抽取一些特征强化学习系列之五:进入实际问题的关键——价值函数近似

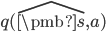
，将这些特征代替状态作为价值函数的输入，即强化学习系列之五:进入实际问题的关键——价值函数近似

或者

强化学习系列之五:进入实际问题的关键——价值函数近似

。这种方法我们称之为价值函数近似。价值函数近似解决了海量状态之后，我们才能实用强化学习算法。

强化学习系列之五:进入实际问题的关键——价值函数近似

文章目录

1. 参数化和目标

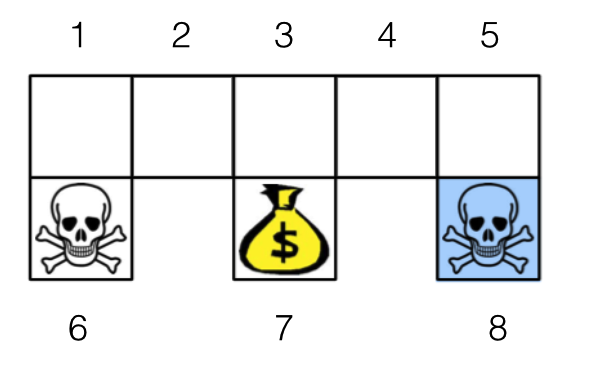
我们又要以机器人找金币为场景介绍价值函数近似。机器人从任意一个状态出发寻找金币，找到金币则获得奖励 1，碰到海盗则损失 1。找到金币或者碰到海盗，机器人都停止。衰减因子强化学习系列之五:进入实际问题的关键——价值函数近似

设为 0.8。

强化学习系列之五:进入实际问题的关键——价值函数近似

机器人找金币只有 9 个状态，但为了介绍价值函数近似，我们就假装状态非常多。我们以四个方向是否有墙作为状态特征，比如状态 1 的特征为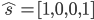强化学习系列之五:进入实际问题的关键——价值函数近似

, 分别表示北 (东、南、西) 方向有 (没有、没有、有) 墙。状态太多的情况下，模型无关的强化学习算法比较有用。模型无关的强化学习算法的工作对象是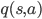强化学习系列之五:进入实际问题的关键——价值函数近似 (有状态特征之后为 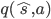), 因此只有状态的特征是不够的。为此我们设定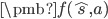特征向量一共分为 |A| 部分，分别对应不同的动作。在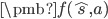特征向量, a 动作部分放上特征，其他动作部分全部置为 0。比如机器人找金币场景，状态 1 采取向北动作的特征向量强化学习系列之五:进入实际问题的关键——价值函数近似如下。

/begin{eqnarray}

/pmb{f(1,'n')} = [/underbrace{1, 0, 0, 1,}_{a='n'} /underbrace{0, 0 , 0 , 0,}_{a='e'} /underbrace{0, 0 , 0 , 0,}_{a='s'} /underbrace{0, 0 , 0 , 0}_{a='w'}]^{T} /nonumber

/end{eqnarray}

搞出特征来了，接下来就用参数计算价值了。我们设定参数向量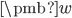强化学习系列之五:进入实际问题的关键——价值函数近似，然后用特征向量和权重向量的内积估计状态-动作价值。

/begin{eqnarray}

q(/hat{s},a) = /pmb{f(/hat{s},a)}^{T} /pmb{w} /nonumber

/end{eqnarray}

这时强化学习其实就是学习参数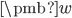强化学习系列之五:进入实际问题的关键——价值函数近似

的值，使得参数化的 q 值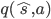强化学习系列之五:进入实际问题的关键——价值函数近似尽量接近最优策略的 q 值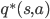，优化目标如下所示。

/begin{eqnarray}

J(/pmb{w}) = min /sum_{s /in S, a /in A}/{ q(/hat{s},a) - q^{*}(s,a)/}^2 /nonumber

/end{eqnarray}

我们用梯度下降法求解这个优化目标。梯度下降法首先要计算梯度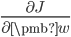强化学习系列之五:进入实际问题的关键——价值函数近似。直接求导可得梯度。

/begin{eqnarray}

/frac{/partial J}{/partial /pmb{w}} &=& /sum_{s /in S, a /in A}/{ q(/hat{s},a) - q^{*}(s,a) /}/pmb{f(/hat{s},a)} /nonumber

/end{eqnarray}

但是状态很多，我们不可能真的按照上面的公式计算梯度 (上面的公式得遍历所有的状态)。实际的方法是让系统探索环境，遇到状态特征强化学习系列之五:进入实际问题的关键——价值函数近似和采取动作 a, 计算梯度然后更新参数。这个类似随机梯度下降。

/begin{eqnarray}

/frac{/partial J}{/partial /pmb{w}}_{/hat{s},a} &=& /{ q(/hat{s},a) - q^{*}(s,a) /}/pmb{f(/hat{s},a)} /nonumber //

/Delta /pmb{w} &=& -/alpha /frac{/partial J}{/partial /pmb{w}}_{/hat{s},a} /nonumber

/end{eqnarray}

参数更新的代码如下所示。

#qfunc 是最优策略的 q 值 #alpha 是学习率 def update(policy, f, a, qfunc, alpha):     pvalue        = policy.qfunc(f, a);     error         = pvalue - tvalue;      fea           = policy.get_fea_vec(f, a);     policy.theta -= alpha * error * fea;

2. 强化学习算法

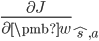
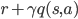
看了上面，你可以会问。计算强化学习系列之五:进入实际问题的关键——价值函数近似

需要最优策略的 q 值，那我们上哪里去找这个值呢? 这是就是该强化学习算法上场了。我们回想一下三个模型无关的强化学习算法，都是让系统探索环境，探索时更新状态-动作价值。在更新时，MC Control 认为该样本的预期收益强化学习系列之五:进入实际问题的关键——价值函数近似

为最优策略的 q 值，让状态-动作价值 q(s,a) 尽量接近。SARSA 认为强化学习系列之五:进入实际问题的关键——价值函数近似

为最优策略的 q 值，Q Learning 认为

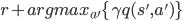
强化学习系列之五:进入实际问题的关键——价值函数近似

。

/begin{eqnarray}

qfunc&=&g_t /quad &MC Control /nonumber //

qfunc&=&r+/gamma q(/hat{s},a) /quad &SARSA /nonumber //

qfunc&=&r+argmax_{a'}/{/gamma q(/hat{s}',a')/} /quad &Q Learning /nonumber

/end{eqnarray}

有了这些想法，我们只需要简单地改变下强化学习算法的更新部分，就可以引入价值函数近似了。新的更新规则是将算法认为的最优策略的 q 值输入参数更新模块。觉个例子，价值函数近似之后的 Q Learning 算法代码如下所示。

def qlearning(grid, policy, num_iter1, alpha):     actions = grid.actions;     gamma   = grid.gamma;     for i in xrange(len(policy.theta)):         policy.theta[i] = 0.1      for iter1 in xrange(num_iter1):         f = grid.start();            #从一个随机非终止状态开始， f 是该状态的特征         a = actions[int(random.random() * len(actions))]         t = False         count = 0          while False == t and count < 100:             t,f1,r      = grid.receive(a)             #t  表示是否进入终止状态             #f1 是环境接受到动作 a 之后转移到的状态的特征。             #r  表示奖励              qmax = -1.0             for a1 in actions:                 pvalue = policy.qfunc(f1, a1);                 if qmax < pvalue:  qmax = pvalue;             update(policy, f, a, r + gamma * qmax, alpha);              f           = f1             a           = policy.epsilon_greedy(f)             count      += 1        return policy;

3. 做个实验

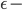
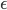
我们用机器人找金币做个实验吧。实验中，我们用了两种特征。一种特征是强特征，也就是上述四个方向是否有墙特征。另一种特征是 id 特征，特征向量长度为状态个数，第 i 个状态的特征向量的第 i 位为 1，其他位置为 0。实验对比了三种算法: MC Control, SARSA 和 Q Learning。强化学习系列之五:进入实际问题的关键——价值函数近似

贪婪策略的

设为 0.2，学习率

强化学习系列之五:进入实际问题的关键——价值函数近似

设为 0.001。和上文一样，算法计算得到的状态(特征)-动作价值和最优策略的状态-动作价值之间的平方差，当做评价指标。实验的结果如下图所示。

强化学习系列之五:进入实际问题的关键——价值函数近似

这个实验结果告诉我们的第一件事就是选好特征。墙特征比 id 特征差。状态2 和 4 都是南北方向有墙，墙特征是一样的，会造成混淆。id 特征就没有这个问题。表现在实验结果上，MC Control 和 SARSA 在墙特征上都不停震荡，同时三种算法在墙特征的表现都不如其在 id 特征上的表现。

Q Learning 一如既往地表现出优越的效果。在墙特征上， Q Learning 不仅没有像 MC Control 和 SARSA 一样震荡，而且效果远远好于它们两者。在 id 特征上， Q Learning 完美拟合了最优策略的状态-动作价值。

4. 总结

实际问题中，状态的数目非常多，因此基于状态-动作价值的强化学习算法不适用。为了解决这个问题，人们提出了价值函数近似的方法。价值函数近似用特征表示状态或者状态-动作，用参数向量计算价值。价值近似之后，我们才算能把强化学习算法应用在实际问题上。本文代码可以在 Github 上找到，欢迎有兴趣的同学帮我挑挑毛病。强化学习系列的下一篇文章将介绍基于梯度的强化学习。

文章结尾欢迎关注我的公众号 AlgorithmDog，每周日的更新就会有提醒哦~

强化学习系列之五:进入实际问题的关键——价值函数近似