【译】小白学SVM系列教程（一）
英文原文链接： SVM - Understanding the math - Part 1 - The margin
译者注：本人研一，项目原因需要了解SVM知识，奈何向量相关知识全都还给本科老师，这一部分完全没看懂，直到看到了国外某博客写的这个SVM系列教程，深入浅出，只要有初中数学基础即可看懂，特别适合我这样的。于是翻译该系列教程，帮助和我一样经历的同学早日掌握SVM。
全系列目录：
-
小白学SVM系列教程（一）—— 间隔（margin）
-
小白学SVM系列教程（二）—— 向量
-
小白学SVM系列教程（三）—— 最优超平面
介绍
这是我写的SVM背后的数学原理系列文章的第一篇。有许多人说要了解SVM，充分的数学背景知识是必要的，不过我将尽量由浅入深慢慢地讲解，以便每一个细节都是清楚明白的，甚至对于初学者来说也能够理解。
支持向量机（SVM）的目标是什么？
支持向量机的目标是找出能够最大化训练集数据间隔（margin）的最优分类超平面。
首先，我们能够从定义中看出SVM需要训练数据，也就是说它是一种监督学习算法。
知道SVM是一种分类算法也是十分重要的，这意味着我们将使用它去预测某个东西是否属于特定的类别。
例如，我们拥有如下的训练数据：
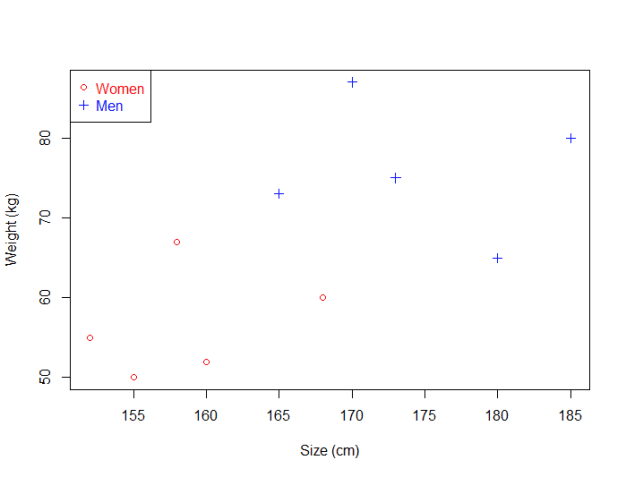我们已经绘制了人群的身高和体重散点图，也用不同的标记区分了男人和女人。
有了这些数据，我们将能够使用SVM回答下面几个问题：
给定一个具体的数据点（身高和体重），这个人是男人还是女人？例如：如果知道某人身高175cm体重80kg，这个人是男人还是女人？
什么是分类超平面？
通过观察上图，我们能够发现分类这些数据是可能的。例如，我们可以描绘一条直线然后所有代表男人的点都在直线的上边，代表女人的点都在直线的下边。
这条直线被称为 分类超平面 ，如下图所示：
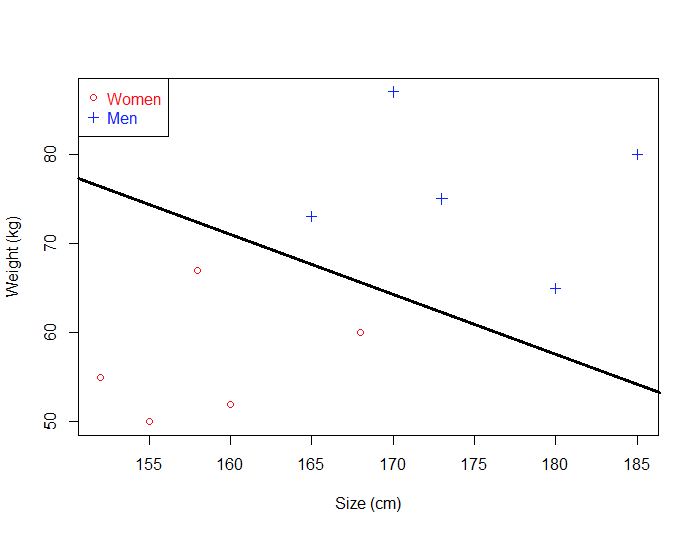
如果它就是一条线，为什么我们称它为超平面呢？
超平面是平面的抽象。
-
在一维空间，超平面是一个点
-
在二维空间，它是一条线
-
在三位空间，它是一个面
-
在更高维度上，你能够称它为超平面
在一维空间中，点L是一个分类超平面。
什么是最优分类超平面？
你能够找到一个分类超平面，但这并不意味着它是最好的那个！在下面的例子中有几个分类超平面，每个都成功地将我们的数据集分类为男人和女人两部分。
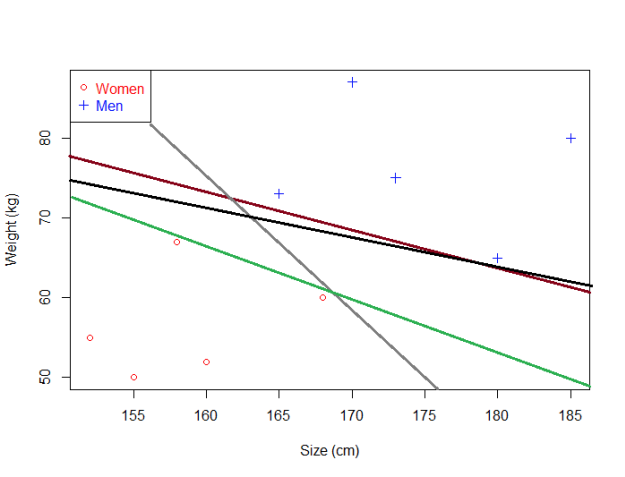
存在许多的分类超平面
假设我们选择绿色的超平面并且使用它给真实数据分类。
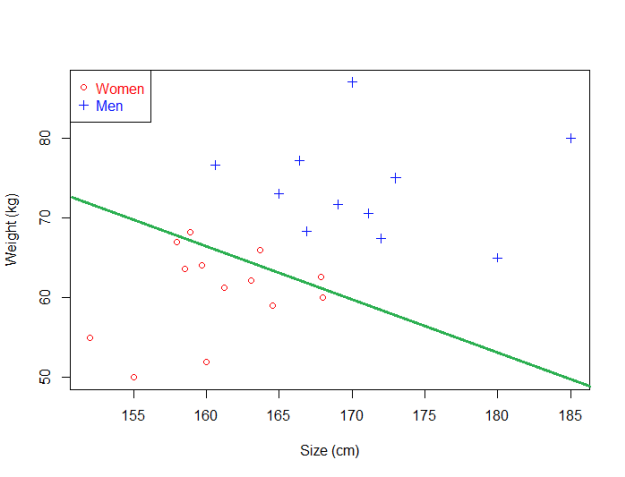
这个超平面并不能够很好的分类数据。
这次，它分类出现了错误。明显，我们能够看出，如果我们选择了一个靠近某一类数据点的超平面，它也许并不能很好地分类数据。
因此我们将会尝试选择一个 尽可能远离每一种类别数据点的 超平面：
这一个看起来更好。当我们用它分类真实数据中时，它仍然进行了完美的分类。
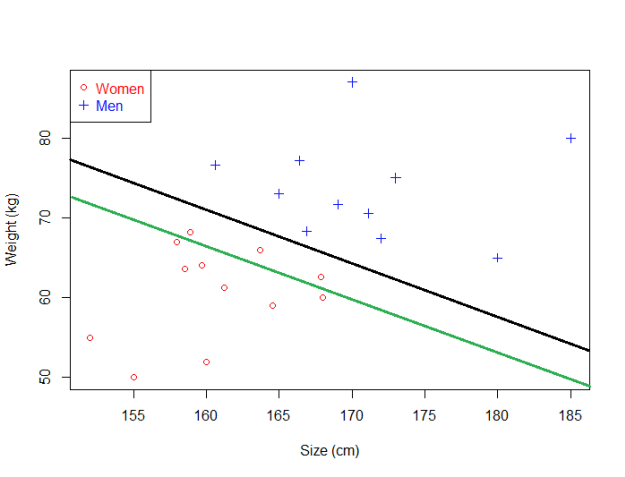黑色的超平面比绿色的超平面分类更准确。
这就是为什么SVM的目标是 寻找最优分类超平面 ：
-
因为它能够正确地分类训练数据
-
同时因为它能更准确地分类尚未出现的数据。
什么是间隔和它是如何帮助选择最优超平面？
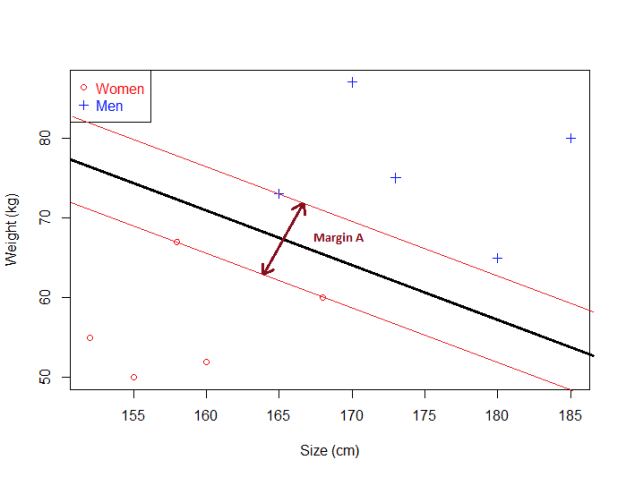
我们的最优超平面的间隔
给定一个超平面，我们能够计算出超平面到最近的一个点的距离。一旦我们算出这个值，如果我们将距离乘以2我们就可以得到 间隔 （margin）。
基本上，间隔是一个“无人区”。在间隔内不存在任何数据点。
对于另一个超平面，间隔将看起来像这样：
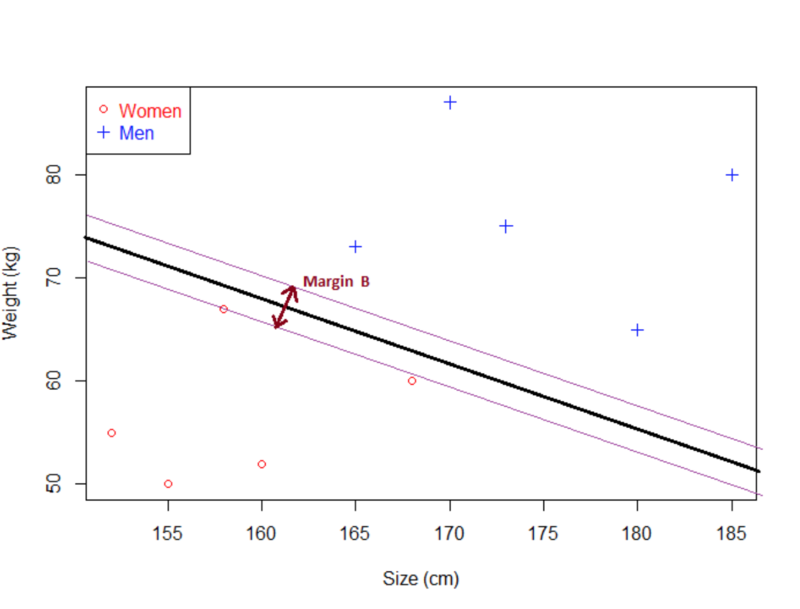
如图所示，间隔B比间隔A小得多。
我们能够观察到以下结果：
-
如果一个超平面十分接近某个数据点，它的间隔将很小
-
超平面距离数据点越远，间隔就越大
这意味着 最优超平面将是拥有最大边距的那个超平面 。
这也是为什么SVM的目标是 找到最大化训练集数据间隔的最优分类超平面 。
到这里关于SVM背后的数学原理的介绍就结束了，目前没有有多少公式，但是在下篇文章我们将增加一些数字然后试着从数学的视角（几何和向量）来进行理解。
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
