转载

拓扑数据分析在机器学习中的应用

机器学习(ML)算法涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。它是人工智能的核心，是使计算机具有智能的根本途径，其应用遍及人工智能的各个领域，它主要使用归纳、综合而不是演绎。而“拓扑数据分析”作为机器学习的一种形式，已经开始被广泛应用。本文简要介绍“拓扑数据分析”在机器学习中的应用以及优势。

什么是拓扑学?

拓扑学是一种几何学，但它研究的并不是大家所熟悉的普通几何性质，而是一类特殊的几何性质，这就是“拓扑性质”，即图形在整体结构上的特性。它与几何图形的大小、形状以及所含线段的曲直等无关。不过，最近拓扑学开始和数据分析相结合，用来发现大数据中的一些隐形的有价值的关系，我们将其称为“拓扑数据分析”(Topological Data Analysis，简称TDA)。

拓扑学中有一个著名的定理Euler多面体定理。这个定理非常简单：对于任意的一个凸多面体，它的面数为f，棱数为l，顶点数为v，那么其必然满足下面的等式：

f-l+v=2

也就是说顶点数与面数之和比棱数多2。

2这个数字，是第一个拓扑数，它标记拓扑等价于球面的几何体。所谓拓扑等价，指的是如果两个几何体可以通过连续拉伸、扭曲、旋转等操作变换到对方(如图1)，这些操作不能是粘合、撕裂，那么这两个几何体称作是拓扑等价的。因此，也有人形象地将拓扑学称为橡皮几何学，因为它研究的性质在图形做弹性形变时是不会改变的。

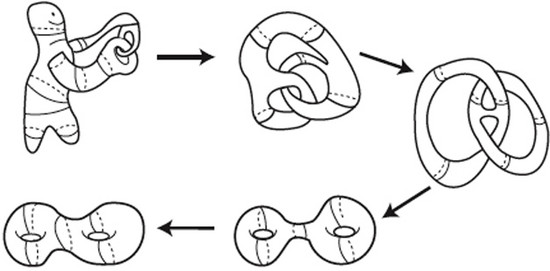
图1 拓扑等价示例

TDA可以有效地捕捉高维数据空间的拓扑信息，已成功地运用到许多领域，例如肿瘤、神经、图像处理和生物物理学等。TDA的成功主要基于两个事实：一是不同数据具有不同的结构，更形象地也可以称之为形状，即每个数据集都含有独特的形状;另一个是数据的形状蕴藏着巨大的研究价值，它能反映数据的大部分特征。以下我们就着重讨论如何刻画“数据的形状”。

从几何的观点来看，降维可看成是挖掘嵌入在高维数据中的低维线性或非线性流形。这种嵌入保留了原始数据的几何特性，即在高维空间中靠近的点在嵌入空间中也互相靠近。举个简单的例子，如图2，左边是点云数据，它与坐标无关，看起来像只手，右边是经过拓扑分析后得到的图像，看起来像“手的骨骼”。

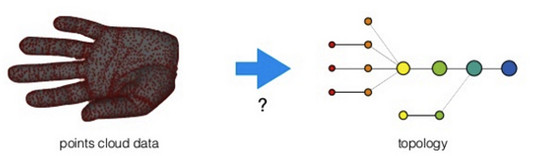
图2 拓扑分析示例

从左边到右边，就完成了拓扑分析“形状的重构”。右图用几个点以及几条边就刻画出了与原数据存在“几分相似”的拓扑图，而TDA要找的就是这“几分相似”，因为这“几分相似”会产生很多有用的信息。

从以上例子可以看出，TDA学习的是数据集的整体特征，对小误差的容忍度很大——即便你的相似度概念在某种程度上存在缺陷，而且它完全不受坐标的限制，在发生变形时，仍能保持原有的性质，能很好地反映数据的形状。这就是TDA的优点-通用性。对于TDA，任何相似性概念都可以拿来使用，但对于ML，你需要一个(或更多)强化的相似性概念，与其他方法一起发挥作用。

与拓扑密不可分的“流形学习”

提到拓扑，就不得不说“流形学习”。“流形”就是在局部与欧氏空间同胚的空间。换言之，它是局部具有欧氏空间性质的空间，能用欧氏距离来进行距离计算。这给降维方法带来了很大的启发：若低维流形嵌入到高维空间中，则数据样本在高维空间的分布虽然看上去非常复杂，但在局部上仍具有欧氏空间的性质。因此可以容易地局部建立降维映射关系，然后设法将局部映射推广到全局。如果将维度降到2或3维，就能对数据进行可视化展示，因此流形学习也可被用于可视化。

“流形学习”是一类借鉴了拓扑流形概念的降维方法，分为线性的和非线性两种：

线性的流形学习方法，如我们熟知的主成份分析(PCA)。

非线性的流形学习方法，包括等距映射(Isomap)、拉普拉斯特征映射(Laplacian Eigenmaps，简称LE)、局部线性嵌入(Locally-linear Embedding，简称LLE)。

本文主要介绍一种比较新的流形学习方法：t-分布邻域嵌入算法(t-Distributed Stochastic Neighbor Embedding，简称t-SNE)。

t-SNE主要基于这样的思想：如果两个数据点在原始空间中距离较近，但它们的两个映射点距离较远，它们就会相互吸引;当它们的两个映射点距离较，则他们会相互排斥。当达到平衡时得到最后的映射，完成原始高维空间与低维映射空间之间的映射关系。

TDA经常与t-SNE算法相结合使用，能达到比较好的效果。下面通过一个TDA与t-SNE处理高维数据的案例来说明。

样本如图3，为MNIST手写数字识别库，它是美国中学生手写的数字数据库，总共有1797张图片，每张图片的大小为8*8，展开之后就是64维，每张图片代表一个样本点，所以样本数据大小为(1797，64)。考虑到高维数据计算余弦距离最快，我们采用余弦距离表示每个样本点的相似度。

图3 MNIST手写数字识别库

图4 t-SNE与TDA相结合的计算结果

图5 t-SNE与TDA相结合的计算结果

利用t-SNE与TDA相结合的算法进行计算，结果如图4和图5所示。点越大说明该集合所含的样本点越多，有边连接的部分说明两个集合相似度比较高。不同的颜色代表原始高维空间与低维映射空间之间的不同映射关系。

简单查看结果，可以发现TDA确实把相似度高的集合连接在了一起，而相似度较低的集合被分开了。从这个例子可以看出，利用TDA做可视化也是一个不错的选择。

TDA的应用比较广泛，Gurjeet Singh的文章[1]中给出了很多有关TDA的应用，例如图6，第一列和第三列代表3D数据，与它们相对应的拓扑图分别放置在第二列和第四列。它们简明地向我们解释着数据中隐藏的形状，从中我们可以得到很多有用信息，这是传统方法无法识别的。

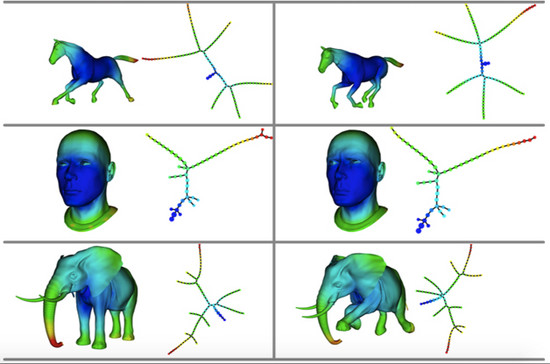
图6 TDA可以简明地解释数据中隐藏的形状

另外，瀚思在帮助客户利用TDA对用户行为进行分析时，发现它的计算时间也相当快。测试样本数据大小为10w*10w，计算时间约为五分钟，而且错误率仅仅为1.3%。这相比传统的方法，看起来相当可观。

总结

TDA是机器学习中一个非常强大的工具，TDA与机器学习方法可以一起使用，得到的效果比使用单个技术更好。更重要的是，它从很大程度上改变了我们分析数据的方式，将拓扑这个纯数学领域的学科与数据分析相结合，是一个很前沿和大胆的技术。笔者相信未来会有更多基于TDA与机器学习的相关算法被提出，并能够成功应用到信息安全领域。