几种常见排序算法

本文介绍几种常见排序算法（选择排序，插入排序，希尔排序，归并排序，快速排序，堆排序），对算法的思路、性质、特点、具体步骤、java实现以及trace图解进行了全面的说明。最后对几种排序算法进行了比较和总结。

写在前面

• 本文所有图片均截图自coursera上普林斯顿的课程 《Algorithms, Part I》 中的Slides

• 相关命题的证明可参考 《算法（第4版）》

• 源码可在 官网 下载,也可以在我的github仓库 algorithms-learning 下载，已经使用maven构建

• 仓库下载： git clone git@github.com:brianway/algorithms-learning.git

基础介绍

Java中很多类已经实现了 Comparable<T> 接口，用户也可自定义类型实现该接口

total order:

• Antisymmetry(反对称性): if v ≤ w and w ≤ v, then v = w.

• Transitivity(传递性): if v ≤ w and w ≤ x, then v ≤ x.

• Totality: either v ≤ w or w ≤ v or both.

注意： The <= operator for double is not a total order ，violates totality: (Double.NaN <= Double.NaN) is false

通用代码：

// Less. Is item v less than w ? private static boolean less(Comparable v, Comparable w) {     return v.compareTo(w) < 0; }  //Exchange. Swap item in array a[] at index i with the one at index j private static void exch(Comparable[] a,, int i, int j) {     Comparable swap = a[i];     a[i] = a[j];     a[j] = swap; } 

初级排序算法

selection sort(选择排序)

思路：

现象：

• 设已排序的和未排序的交界处为 ↑，则每次循环， ↑ 从左往右移动一个位置

• ↑ 左边的元素（包括↑）固定了，且升序

• ↑ 右边的任一元素全部比左边的所有元素都大

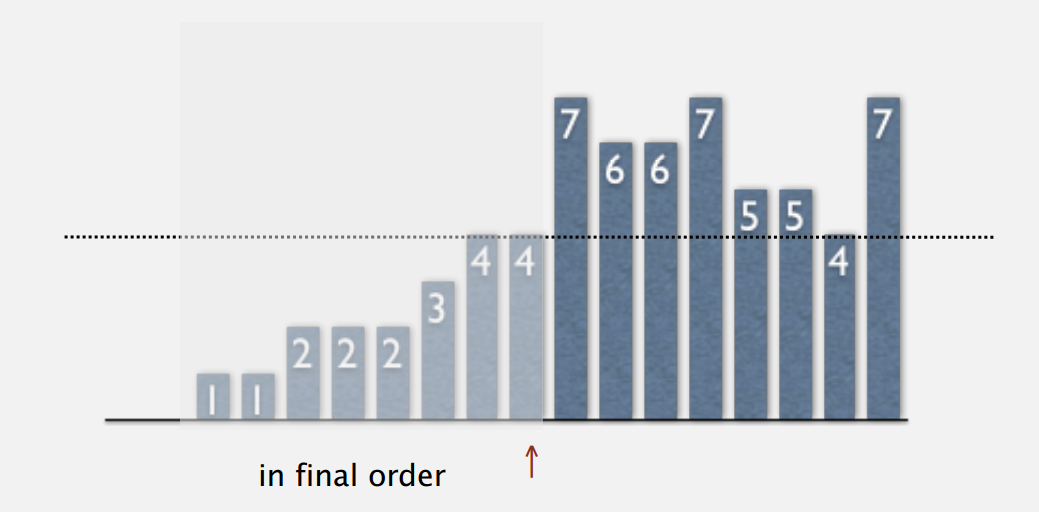
步骤：

• move the pointer to the right

• indentify index of minimun entry on right

• exchange into positon

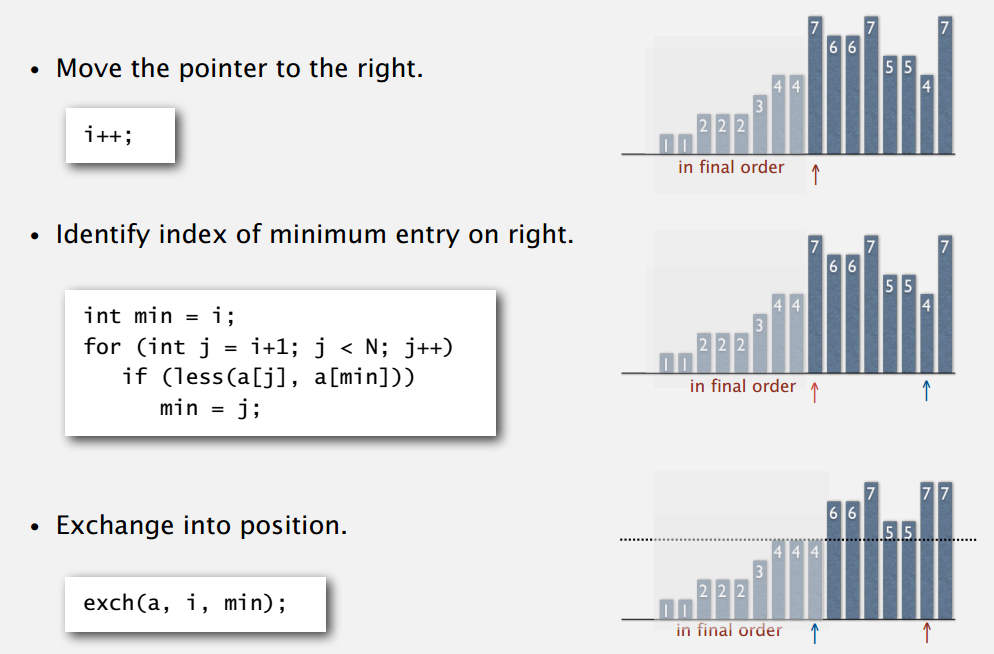
java实现：

public static void sort(Comparable[] a) {     int N = a.length;     for (int i = 0; i < N; i++) {         int min = i;         for (int j = i+1; j < N; j++) {             if (less(a[j], a[min])) min = j;         }         exch(a, i, min);     } }

特点：

• 运行时间和输入无关，无论输入是已排序，时间复杂度都是O(n^2)

• 数据移动最少，交换的次数和数组大小是线性关系

insertion sort(插入排序)

思路：

现象：

• 设已排序的和未排序的交界处为 ↑，则每次循环， ↑ 从左往右移动一个位置

• ↑ 左边的元素（包括↑）且升序，但位置不固定(因为后续可能会因插入而移动)

• ↑ 右边的元素还不可见

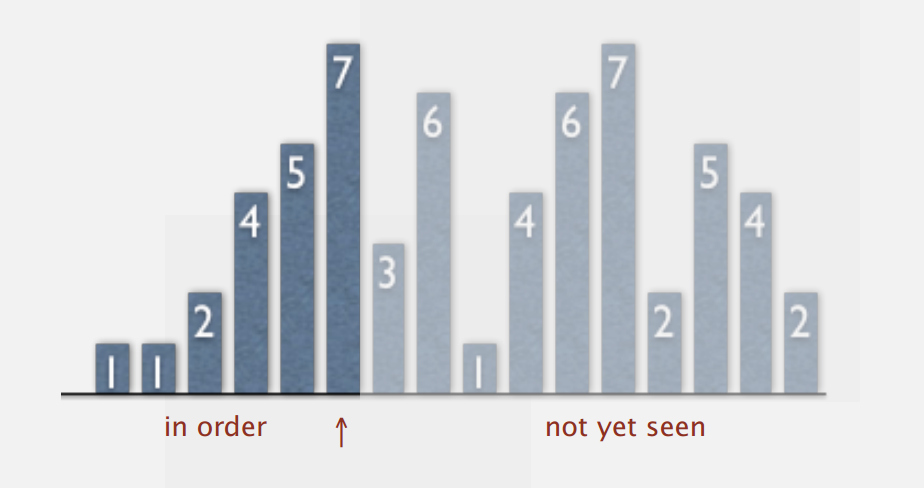
步骤：

• Move the pointer to the right.

• Moving from right to left, exchange a[i] with each larger entry to its left.

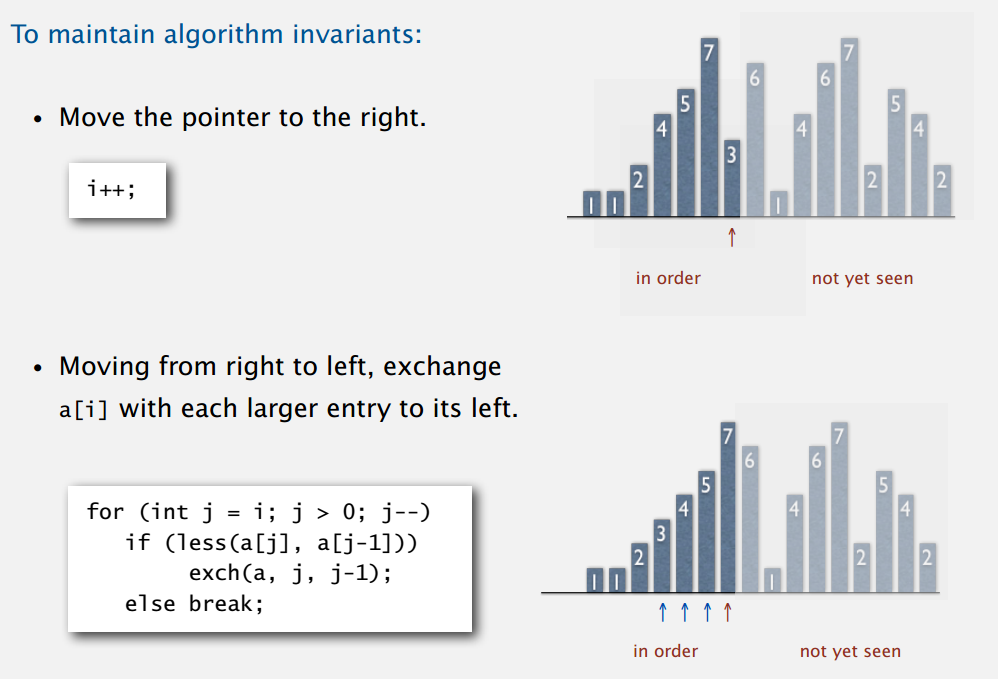
java实现：

public static void sort(Comparable[] a) {     int N = a.length;     for (int i = 0; i < N; i++) {         for (int j = i; j > 0 && less(a[j], a[j-1]); j--) {             exch(a, j, j-1);         }     } }

inversion（倒置）：An inversion is a pair of keys that are out of order

部分有序：An array is partially sorted if the number of inversions is ≤ c N.

特点：

• 运行时间和输入有关，当输入已排序时，时间复杂度是O(n);

• For partially-sorted arrays, insertion sort runs in linear time.(交换的次数等于输入中倒置(inversion)的个数)

• 插入排序适合部分有序数组，也适合小规模数组

ShellSort(希尔排序)

希尔排序是基于插入排序的。

思路：

现象：

• 数组中任意间隔为h的元素都是有序的

• A g-sorted array remains g-sorted after h-sorting it.

性质：

java实现：

public static void sort(Comparable[] a) {     int N = a.length;      // 3x+1 increment sequence:  1, 4, 13, 40, 121, 364, 1093, ...      int h = 1;     while (h < N/3) h = 3*h + 1;       while (h >= 1) {         // h-sort the array         for (int i = h; i < N; i++) {             for (int j = i; j >= h && less(a[j], a[j-h]); j -= h) {                 exch(a, j, j-h);             }         }         h /= 3;     } }

shuffing(不是排序算法)

shuffle sort思路

Knuth shuffle demo

correct variant: between i and N – 1

• Mergesort--Java sort for objects.

• Quicksort--Java sort for primitive types.

下面看看这两种排序算法

merge sort(归并排序)

思路：

Abstract in-place merge(原地归并的抽象方法)

步骤：

• 先将所有元素复制到 aux[] 中，再归并回 a[] 中。

• 归并时的四个判断：

  • 左半边用尽(取右半边元素)

  • 右半边用尽(取左半边元素)

  • 右半边的当前元素 小于 左半边的当前元素(取右半边的元素)

  • 右半边的当前元素 大于/等于 左半边的当前元素(取左半边的元素)

merging java实现：

 // stably merge a[lo .. mid] with a[mid+1 ..hi] using aux[lo .. hi] private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {     // precondition: a[lo .. mid] and a[mid+1 .. hi] are sorted subarrays       // copy to aux[]     for (int k = lo; k <= hi; k++) {         aux[k] = a[k];      }      // merge back to a[]     int i = lo, j = mid+1;     for (int k = lo; k <= hi; k++) {         if      (i > mid)              a[k] = aux[j++];         else if (j > hi)               a[k] = aux[i++];         else if (less(aux[j], aux[i])) a[k] = aux[j++];         else                           a[k] = aux[i++];     } }

Top-down mergesort(自顶向下的归并排序)

mergesort java实现：

// mergesort a[lo..hi] using auxiliary array aux[lo..hi] private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {     if (hi <= lo) return;     int mid = lo + (hi - lo) / 2;     sort(a, aux, lo, mid);  //将左边排序     sort(a, aux, mid + 1, hi);  //将右边排序     merge(a, aux, lo, mid, hi); //归并结果 }

自顶向下的归并排序的轨迹图

由图可知，原地归并排序的大致趋势是，先局部排序，再扩大规模；先左边排序，再右边排序；每次都是左边一半局部排完且merge了，右边一半才开始从最局部的地方开始排序。

改进

• 对小规模子数组使用插入排序

• 测试数组是否已经有序（左边最大<右边最小时，直接返回）

• 不将元素复制到辅助数组(节省时间而非空间)

Bottom-up mergesort(自底向上的归并排序)

思路：

java实现：

public class MergeBU{    private static void merge(...){ /* as before */ }      public static void sort(Comparable[] a){      int N = a.length;      Comparable[] aux = new Comparable[N];      for (int sz = 1; sz < N; sz = sz+sz)      for (int lo = 0; lo < N-sz; lo += sz+sz)      merge(a, aux, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1));    } }

自底向上的归并排序的轨迹图

由图可知，自底向上归并排序的大致趋势是，先局部排序，逐步扩大到全局排序；步调均匀，稳步扩大

quicksort

思路：

• entry a[j] is in place

• no larger entry to the left of j

• no smaller entry to the right of j

其中很重要的一步就是 Partition(切分) ，这个过程使得满足以下三个条件:

• 对于某个j,a[j]已经排定;

• a[lo]到a[j-1]中的所有元素都不大于a[j];

• a[j+1]到a[hi]中的所有元素都不小于a[j];

partition java实现

// partition the subarray a[lo..hi] so that a[lo..j-1] <= a[j] <= a[j+1..hi] // and return the index j. private static int partition(Comparable[] a, int lo, int hi) {     int i = lo;     int j = hi + 1;     Comparable v = a[lo];     while (true) {           // find item on lo to swap         while (less(a[++i], v))             if (i == hi) break;          // find item on hi to swap         while (less(v, a[--j]))             if (j == lo) break;      // redundant since a[lo] acts as sentinel          // check if pointers cross         if (i >= j) break;          exch(a, i, j);     }      // put partitioning item v at a[j]     exch(a, lo, j);      // now, a[lo .. j-1] <= a[j] <= a[j+1 .. hi]     return j; }

快排java实现：

public static void sort(Comparable[] a) {     StdRandom.shuffle(a);     sort(a, 0, a.length - 1); }  // quicksort the subarray from a[lo] to a[hi] private static void sort(Comparable[] a, int lo, int hi) {      if (hi <= lo) return;     int j = partition(a, lo, hi);     sort(a, lo, j-1);     sort(a, j+1, hi);     assert isSorted(a, lo, hi); }

快排的轨迹图

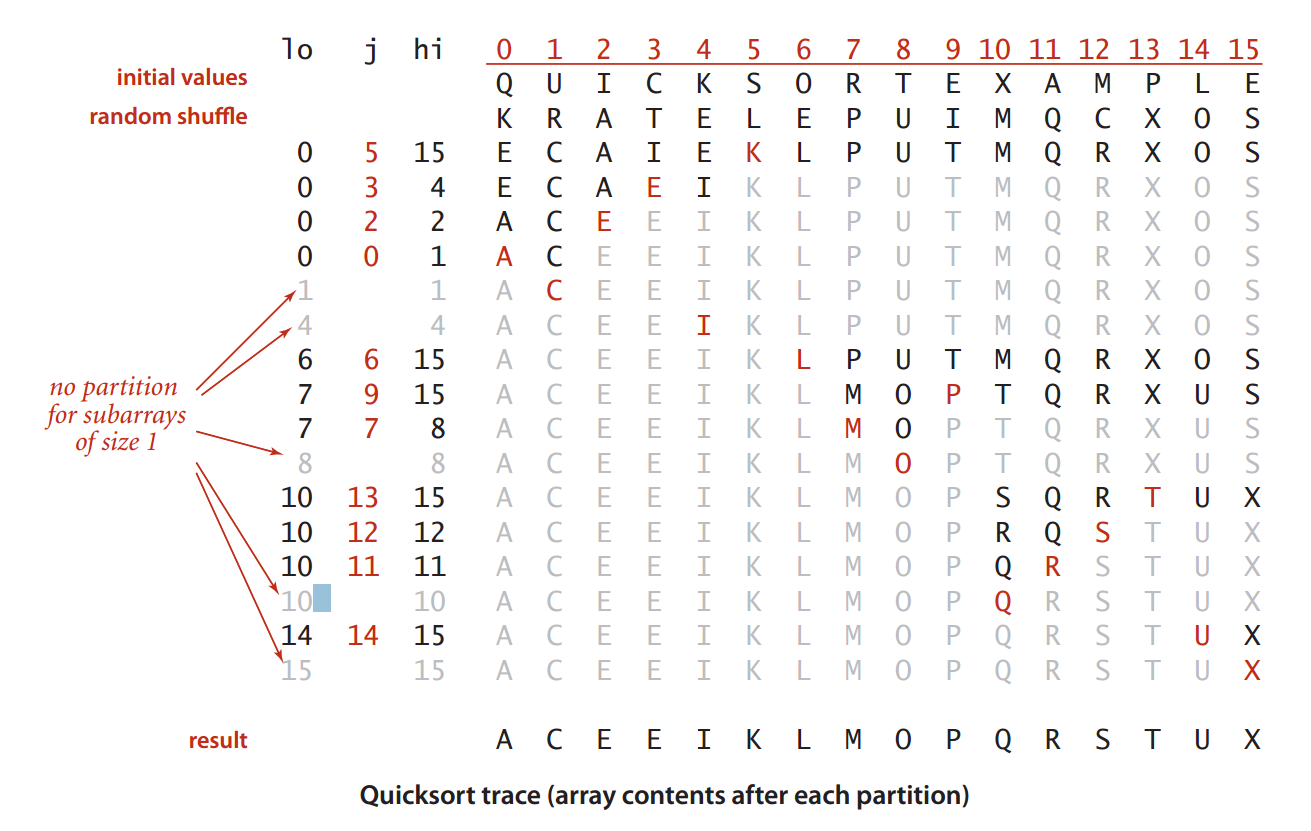
由图可知，和归并排序不同，快排的大致趋势是，先全局大体有个走势——左边比右边小，逐步细化到局部；也是先左后右；局部完成时全部排序也就完成了。

一些实现的细节：

• 原地切分：不使用辅助数组

• 别越界：测试条件(j == lo)是冗余的(a[lo]不可能比自己小)；

• 保持随机性：初始时的随机打乱跟重要

• 终止循环

• 处理切分元素值有重复的情况：这里可能出问题

性质：

• 快排是in-place的

• 快排不稳定

改进

• 对小规模子数组使用插入排序

• 三取样切分

三向切分的快速排序

思路：

• (a[i] < v): exchange a[lt] with a[i]; increment both lt and i

• (a[i] > v): exchange a[gt] with a[i]; decrement gt

• (a[i] == v): increment i

主要是通过增加一个指针来实现的。普通的快拍只有lo和high两个指针，故只能记录 大于 (high右边)和 小于 (lo左边)两个区间， 等于 只能并入其中一个；这里增加了使用了lt,i,gt三个指针，从而达到记录 大于 (gt右边)、 小于 (lt左边)和 等于 (lt和i之间)三个区间。

三切分的示意图

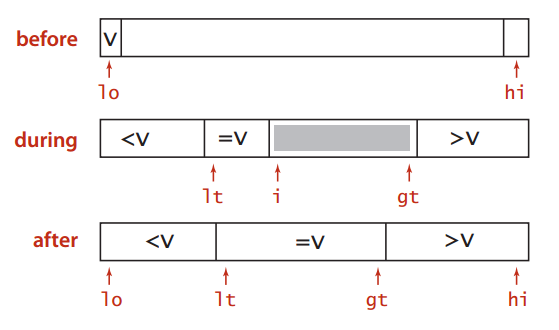
三向切分的java实现：

// quicksort the subarray a[lo .. hi] using 3-way partitioning private static void sort(Comparable[] a, int lo, int hi) {      if (hi <= lo) return;     int lt = lo, gt = hi;     Comparable v = a[lo];     int i = lo;     while (i <= gt) {         int cmp = a[i].compareTo(v);         if      (cmp < 0) exch(a, lt++, i++);         else if (cmp > 0) exch(a, i, gt--);         else              i++;     }      // a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi].      sort(a, lo, lt-1);     sort(a, gt+1, hi); }

Heapsort(堆排序)

思路：

• swim:由下至上的堆有序化

• sink:由上至下的对有序化

堆排序主要分为两个阶段：

1. 堆的构造

2. 下沉排序

java实现如下：

public static void sort(Comparable[] pq) {     int N = pq.length;     //堆的构造     for (int k = N/2; k >= 1; k--)         sink(pq, k, N);          //下沉排序     while (N > 1) {         exch(pq, 1, N--);         sink(pq, 1, N);     } }

堆排序的轨迹图

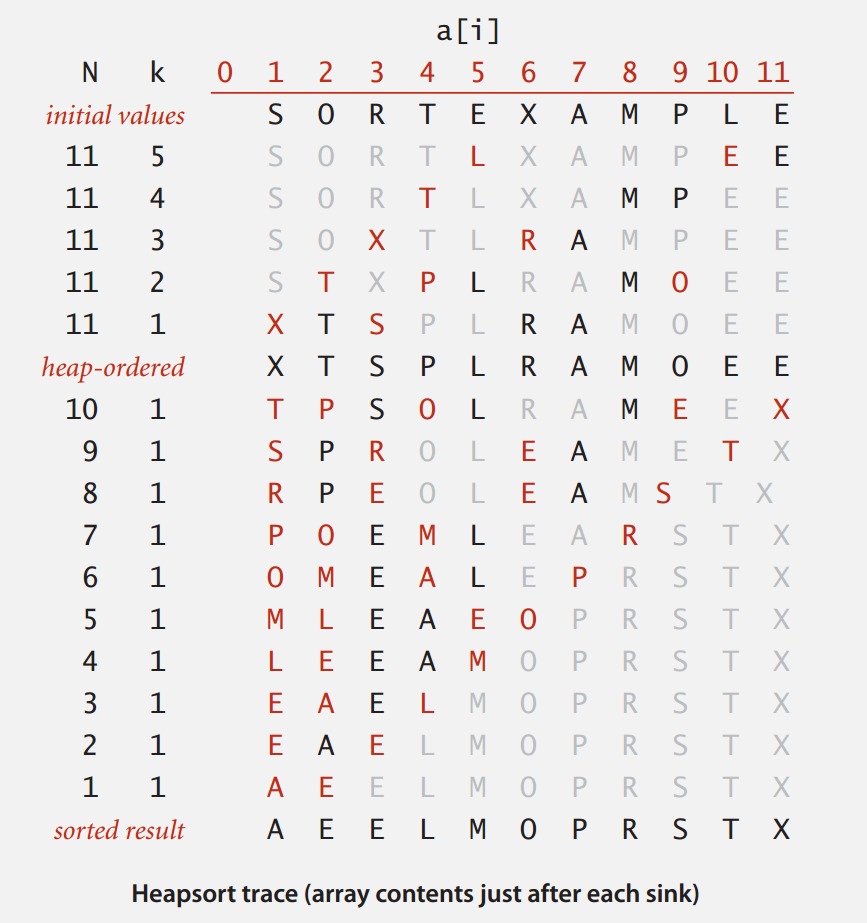
由图看出，堆排序的趋势是，堆构造阶段，大致是降序的走势，到了下沉阶段，从右到左（或者说从后往前）逐步有序

Significance： In-place sorting algorithm with N log N worst-case.

• Mergesort: no, linear extra space.

• Quicksort: no, quadratic time in worst case

缺点

• Inner loop longer than quicksort’s.

• Makes poor use of cache memory.

• Not stable(不稳定)

总结和比较

排序算法总结表

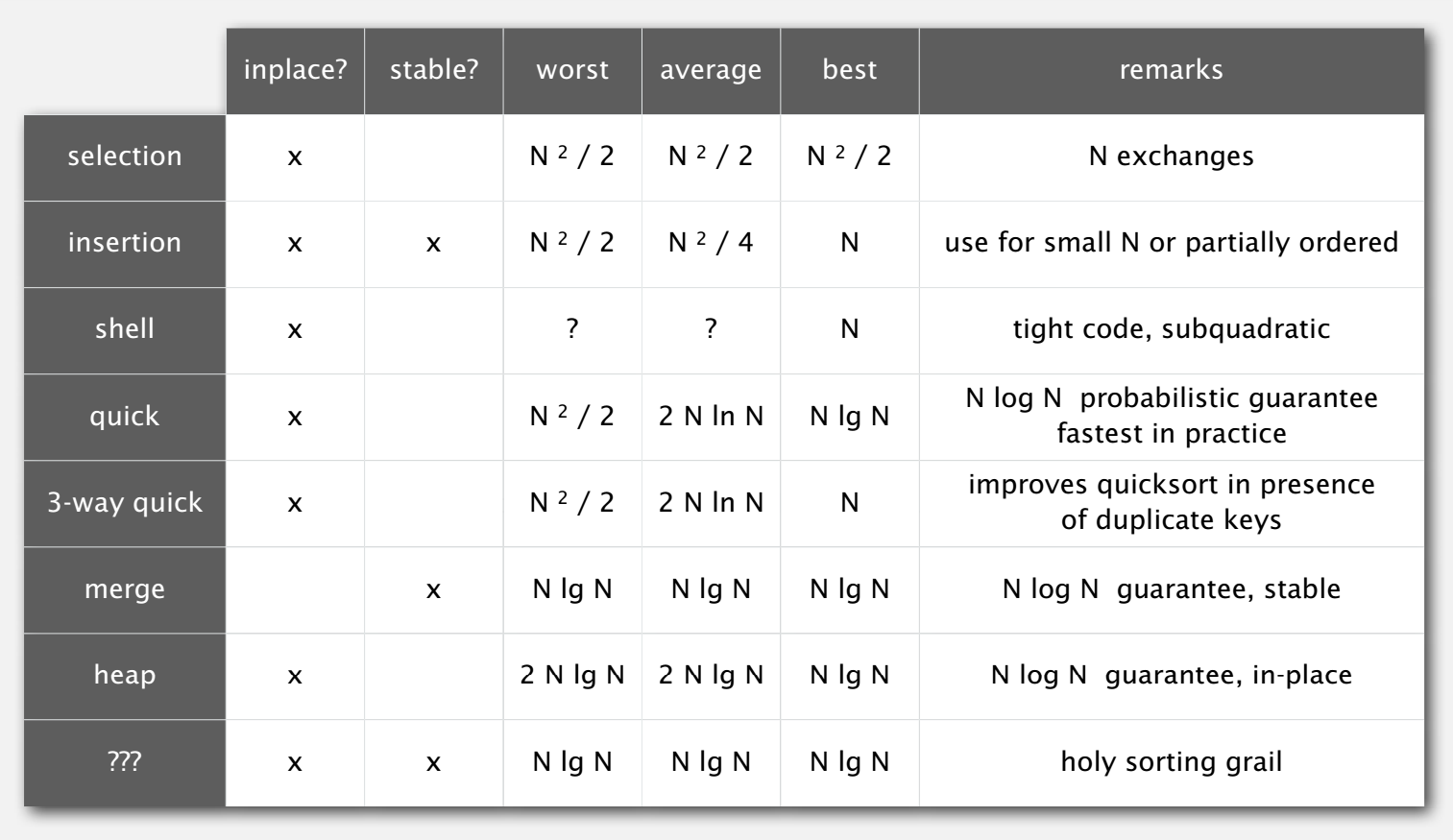
最好情况和最坏情况：参见上面的表格

关于稳定性：

• 稳定性，插入排序，归并排序

• 不稳定：选择排序，快排，希尔排序，堆排序

• 原因： Long-distance exchange

关于额外空间：除了归并排序需要线性的额外空间，其他都是in-place的

命题

• 对于长度为N的数组，选择排序需要N^2/2次比较和N次交换(pf见P156)

• 对于随机排列的长度为N的且主键不重复的数组（pf见P157）

  • 平均情况下插入排序需要~N^2/4次比较和~N^2/4次交换

  • 最坏情况下需要~N^2/2次比较和~N^2/2次交换，

  • 最好情况下需要N-1次比较和0次交换。

• Mergesort uses at most N lg N compares and 6 N lg N array accesses to sort any array of size N. (pf见P173)

• Mergesort uses extra space proportional to N.(The array aux[] needs to be of size N for the last merge.)

• Any compare-based sorting algorithm must use at least lg ( N ! ) ~ N lg N compares in the worst-case.(pf见P177)

• 长度为N的无重复数组排序，快速排序平均需要~2N ln N 次比较（以及1/6即1/3 N ln N的交换）

  • 最多需要约N^2/2次比较

  • 最少需要~N lg N 次比较

• 用下沉操作由N个元素构造堆只需少于2N次比较以及少于N次交换(pf见P206)

• 将N个元素排序，堆排序只需少于（2NlgN+2N）次比较以及一半次数的交换(pf见P208)