转载

强化学习系列之六:策略梯度 | AlgorithmDog

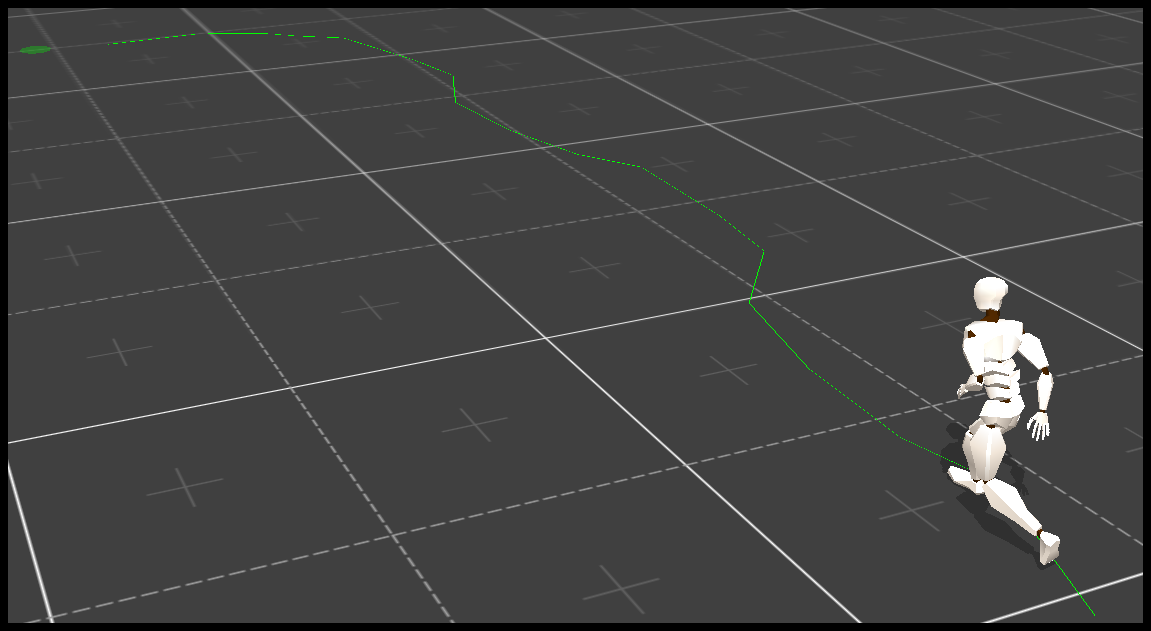
上一篇文章介绍价值函数近似，用模型拟合价值函数。这篇文章我们介绍梯度策略，用模型直接拟合策略强化学习系列之六:策略梯度 | AlgorithmDog

1. 策略参数化

强化学习有两种场景。一种是离散的强化学习场景。在这种场景下，我们从状态抽取状态特征向量

$/hat{s}$ 。和价值函数近似，我们让 $/pmb{f(/hat{s},a)}$ 特征向量一共有 |A| 部分，分别对应不同的动作。在 $/pmb{f(/hat{s},a)}$ 特征向量, a 动作对应位置放 $/hat{s}$ 特征，其他动作对应位置为 0。设定参数 $/pmb{w}$ 。
/begin{eqnarray}
/pi_{/pmb{w}}(/hat{s},a) = /frac{exp(/pmb{f(/hat{s},a)}^{T} /pmb{w})}{/sum_{a' /in A}exp(/pmb{f(/hat{s},a')}^{T} /pmb{w})} /nonumber
/end{eqnarray}
其中 $/pi_{/pmb{w}}(/hat{s},a)$ 表示遇到状态特征 $/hat{s}$ 采取动作 a 的概率。策略用了著名的 Softmax 函数，因此也被称为 softmax 策略。容易求得 Softmax 函数对数的梯度。
/begin{eqnarray}
/bigtriangledown_{/pmb{w}}log/pi_{/pmb{w}}(/hat{s},a) = /pmb{f(/hat{s},a)} - /sum_{a' /in A}/pi_{/pmb{w}}(/hat{s},a')/pmb{f(/hat{s},a')} /nonumber
/end{eqnarray}

def update_softmaxpolicy(policy, f, a, qvalue, alpha):      fea  = policy.get_fea_vec(f,a);     prob = policy.pi(f);          delte_logJ = fea;     for i in xrange(len(policy.actions)):         a1          = policy.actions[i];         fea1        = policy.get_fea_vec(f,a1);         delta_logJ -= fea1 * prob[i];      policy.theta -= alpha * delta_logJ * qvalue;

另一种是连续的强化学习场景。在连续强化学习场景下，我们也是从状态抽取状态特征向量

$/hat{s}$ ，然后设定一个参数向量 $/pmb{w}$ ，然后用特征和参数计算不同动作的概率。

/begin{eqnarray}
/pi_{/pmb{w}}(/hat{s},a) = /frac{1}{/sqrt{2/pi}}exp(-/frac{(a-/pmb{/hat{s}}^{T} /pmb{w})^2}{2}) /nonumber
/end{eqnarray}
其中动作 a 是一个实数值。策略用了标准差为 1 的高斯分布，因此该策略被称为高斯策略。容易求得高斯策略的对数梯度。

/begin{eqnarray}
/bigtriangledown_{/pmb{w}}log/pi_{/pmb{w}}(/hat{s},a) = (a - /pmb{/hat{s}}^{T} /pmb{w}) /pmb{/hat{s}}/nonumber
/end{eqnarray}

强化学习就是学习参数

$/pmb{w}$ 的值。那么我们按什么样的目标学习参数 $/pmb{w}$ 呢? 我们有如下三种目标。其中第一个目标适用于每次从一个开始状态出发的强化学习，另外两种目标适用于其他场景。

/begin{eqnarray}
J_1(/pmb{w}) &=& V^{/pi_{/pmb{w}}}(s1) = E_{/pi_{/pmb{w}}}[v1] /nonumber //
J_{avV}(/pmb{w}) &=& /sum_{s} d^{/pi_{/pmb{w}}}(s) V^{/pi_{/pmb{w}}}(s) /nonumber //
J_{avR}(/pmb{w}) &=& /sum_{s} d^{/pi_{/pmb{w}}}(s) /sum_{a} /pi_{/pmb{w}}(s,a) R_{s,a} /nonumber
/end{eqnarray}

其中

$d^{/pi_{/pmb{w}}}$ 是策略 $/pi_{/pmb{w}}$ 稳定概率。虽然我们有三种目标函数，但是下面的策略梯度定理揭示这些目标函数的梯度是一致。只要我们求得梯度，就可以应用梯度下降相关算法了。

根据策略梯度定理，我们只要计算出

$/bigtriangledown_{/pmb{w}}log/pi_{/pmb{w}}(/hat{s},a)$ 和价值 $q(/hat{s},a)$ ，就可以求解策略梯度优化问题了。Softmax 和高斯策略的 $/bigtriangledown_{/pmb{w}}log/pi_{/pmb{w}}(/hat{s},a)$ 计算公式在上面已经介绍了。那怎么求解价值 $q(/hat{s},a)$ 呢？

2. 策略梯度算法

为了求解策略梯度优化问题，我们需要计算

$/bigtriangledown_{/pmb{w}}log/pi_{/pmb{w}}(/hat{s},a)$ 和价值 $q(/hat{s},a)$ $q(/hat{s},a)$ 。按照上述内容，我们能够求得 $/bigtriangledown_{/pmb{w}}log/pi_{/pmb{w}}(/hat{s},a)$ ，那怎么求解价值 $q(/hat{s},a)$ 呢？

2.1 MC Policy Gradient

蒙特卡罗策略梯度适用于插曲式的强化学习场景。插曲式强化学习场景中，系统会从一个固定或者随机起始状态出发，经过一定的过程之后，进入一个终止状态。比如，机器人找金币例子就是插曲式强化学习场景。蒙特卡罗策略梯度让系统探索环境，生成一个从起始状态到终止状态的状态-动作-奖励序列。

/begin{eqnarray}
s_1,a_1,r_1,.....,s_T,a_T,r_T
/end{eqnarray}

在第 t 时刻，我们让

$g_t = r_t+/gamma r_{t+1}+...$ 等于 q(s_t,a)，从而求解策略梯度优化问题。蒙特卡罗策略梯度代码如下。

def mc(grid, policy, num_iter1, alpha):     actions = grid.actions;     gamma   = grid.gamma;     for i in xrange(len(policy.theta)):         policy.theta[i] = 0.1      for iter1 in xrange(num_iter1):          f_sample = []         a_sample = []         r_sample = []                     f = grid.start()         t = False         count = 0         while False == t and count < 100:             a = policy.take_action(f)             t, f1, r  = grid.receive(a)             f_sample.append(f)             r_sample.append(r)             a_sample.append(a)             f = f1                         count += 1           g = 0.0         for i in xrange(len(f_sample)-1, -1, -1):             g *= gamma             g += r_sample[i];                  for i in xrange(len(f_sample)):             update(policy, f_sample[i], a_sample[i], g, alpha)              g -= r_sample[i];             g /= gamma;               return policy

2.2 Actor-Critic

价值函数近似的强化学习算法用于估计状态-动作价值 q(s,a)。策略梯度算法引入价值函数近似提供价值是一个很好的思路。这时候，算法分为两个部分：Actor 和 Critic。Actor 更新策略， Critic 更新价值。Critic 就可以用之前介绍的 SARSA 或者 QLearning 算法。下面是 SARSA 算法代码示例。

def sarsa(grid, policy, value, num_iter1, alpha):     actions = grid.actions;     gamma   = grid.gamma;     for i in xrange(len(policy.theta)):         value.theta[i]  = 0.1         policy.theta[i] = 0.0;      for iter1 in xrange(num_iter1):         f = grid.start();         a = actions[int(random.random() * len(actions))]         t = False         count = 0          while False == t and count < 100:             t,f1,r      = grid.receive(a)             a1          = policy.take_action(f1)             update_value(value, f, a, r + gamma * value.qfunc(f1, a1), alpha);             update_policy(policy, f, a, value.qfunc(f,a), alpha);              f           = f1             a           = a1             count      += 1      return policy;

3. 为什么要有策略梯度

策略梯度的第一个优势是其能够处理连续场景。价值函数近似就不适用了连续的强化学习场景。因为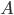强化学习系列之六:策略梯度 | AlgorithmDog

$A$ 是一个无限集合的情况下，我们无法计算 $argmax_{a /in A}q(s,a)$ 了。但如果我们使用的是策略梯度， $/pi(s)$ 输出实数值。当然这一部分可以通过改进价值函数形式的方式解决。

策略梯度的另一好处是概率化输出。在预测时，价值函数近似应用了贪婪策略或者

$/epsilon-$ 贪婪策略，选择价值最大的方向。有时候这可能会导致问题。还是拿机器人找金币做例子（如下图所示），状态特征是北（东，南，西）方向是否面对墙。状态 2 和状态 4 的状态特征一样，贪婪策略或者 $/epsilon-$ 贪婪策略采取相同动作。如果动作是向右，则状态 4 之后会陷入 4 和 5 之间的循环。如果动作是向左，则状态 2 之后会陷入 1 和 2 之间的循环。但是如果我们采用策略梯度，在状态 2 和状态 4，学习到的策略输出向右和向左动作的概率都是 0.5，从而不会陷入循环。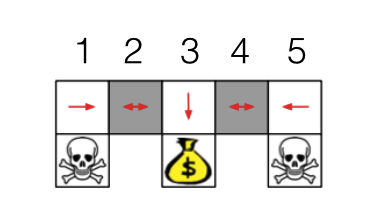

5. 总结

本文是强化学习系列的最后一篇啦，介绍了梯度策略相关知识。本文代码可以在 Github 上找到，欢迎有兴趣的同学帮我挑挑毛病。由于我能力有限，强化学习系列只是对强化学习做了简单介绍，而无法深入探讨强化学习研究中的问题。我在后续工作学习有所收获，会在第一时间分享出来。

最后欢迎关注我的公众号 AlgorithmDog，每周日的更新就会有提醒哦~

原文 http://www.algorithmdog.com/rl-policy-gradient

正文到此结束

所属分类：编程技术

本文标签： DOM git App Action ip CTO 文章 update 时间 http 代码 src GitHub 总结 UI 参数 tar value
版权声明： 本文为互联网转载文章，出处已在文章中说明(部分除外)。如果侵权，请联系本站长删除，谢谢。
本文海报： 生成海报一生成海报二