转载

算法（5）：队列

新学期开始了，小哈是小哼的新同桌（小哈是个小美女哦~），小哼向小哈询问QQ号，小哈当然不会直接告诉小哼啦，原因嘛你懂的。所以小哈给了小哼一串加密过的数字，同时小哈也告诉了小哼解密规则。规则是这样的：首先将第1个数删除，紧接着将第2个数放到这串数的末尾，再将第3个数删除并将第4个数再放到这串数的末尾，再将第5个数删除……直到剩下最后一个数，将最后一个数也删除。按照刚才删除的顺序，把这些删除的数连在一起就是小哈的QQ啦。现在你来帮帮小哼吧。小哈给小哼加密过的一串数是“6 3 1 75 8 9 2 4”。

算法（5）：队列

OK，现在轮到你动手的时候了。快去找出9张便签或小纸片，将“6 3 1 75 8 9 2 4”这9个数分别写在9张便签上，模拟一下解密过程。如果你没有理解错解密规则的话，解密后小哈的QQ号应该是“6 1 5 94 7 2 8 3”。

其实解密的过程就像是将这些数“排队”。每次从最前面拿两个，第1个扔掉，第2个放到尾部。具体过程是这样的：刚开始这串数是“6 3 1 75 8 9 2 4”，首先删除 6 并将3放到这串数的末尾，这串数更新为“1 7 5 89 2 4 3”。接下来删除 1 并将7放到末尾，即更新为“5 8 9 24 3 7”。再删除 5 并将8放到末尾即“9 2 4 3 7 8”，删除 9 并将2放到末尾即“4 3 7 8 2”，删除 4 并将3放到末尾即“7 8 2 3”，删除 7 并将8放到末尾即“2 3 8”，删除 2 并将3放到末尾即“8 3”，删除 8 并将3放到末尾即“3”，最后删除 3 。因此被删除的顺序是“ 6 1 5 9 4 7 2 8 3 ”，这就是小哈的QQ号码了，你可以加她试试看^_^。

既然现在已经搞清楚了解密法则，不妨自己尝试一下去编程，我相信你一定可以写出来的。

首先需要一个数组来存储这一串数即intq[101]。并初始化这个数组即intq[101]={0,6,3,1,7,5,8,9,2,4};（此处初始化是我多写了一个0，用来填充q[0]，因为我比较喜欢从q[1]开始用，对数组初始化不是很理解的同学可以去看下我的上一本书《啊哈C！思考快你一步》）接下来就是模拟解密的过程了。

解密的第一步是将第一个数删除，你可以想一下如何在数组中删除一个数呢？最简单的方法是将所有后面的数都往前面挪动一位，将前面的数覆盖。就好比我们在排队买票，最前面的人买好离开了，后面所有的人就需要全部向前面走一步，补上之前的空位，但是这样的做法很耗费时间。

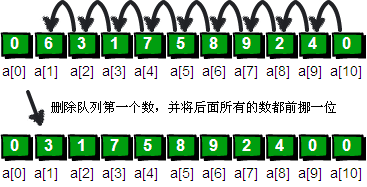
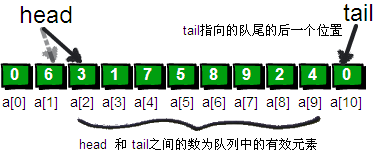
算法（5）：队列

在这里，我将引入两个整型变量head和tail。head用来记录队列的队首（即第一位），tail用来记录队列的队尾（即最后一位）的下一个位置。你可能会问为什么tail不直接记录队尾，却要记录队尾的下一个位置呢？这是因为当队列当中只剩下一个元素时，队首和队尾重合会带来一些麻烦。我们这里规定队首和队尾重合时，队列为空。

现在有9个数，9个数全部放入队列之后head=1;tail=10;此时head和tail之间的数就是目前队列中“有效”的数。如果要删除一个数的话，就将head++就OK了，这样仍然可以保持head和tail之间的数为目前队列中“有效”的数。这样做虽然浪费了一个空间，却节省了大量的时间，这是非常划算的。新增加一个数也很简单，把需要增加的数放到队尾即q[tail]之后再tail++就欧克啦。

算法（5）：队列

我们来小结一下，在队首删除一个数的操作是head++;

在队尾增加一个数（假设这个数是x）的操作是q[tail]=x;tail++;

整个解密过程，请看下面这个霸气外漏的图。

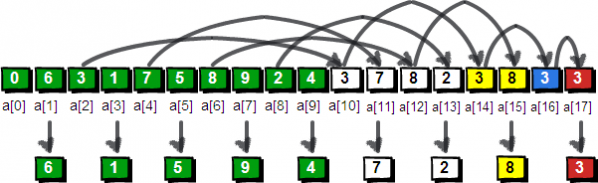
算法（5）：队列

最后的输出就是6 1 5 94 7 2 8 3，代码实现如下。

#include <stdio.h>
int main()
{
int q[102]={0,6,3,1,7,5,8,9,2,4},head,tail;
int i;
//初始化队列
head=1;
tail=10; //队列中已经有9个元素了，tail执向的队尾的后一个位置
while(head<tail) //当队列不为空的时候执行循环
{
//打印队首并将队首出队
printf("%d ",q[head]);
head++;
//先将新队首的数添加到队尾
q[tail]=q[head];
tail++;
//再将队首出队
head++;
}
getchar();getchar();
return 0;
}

复制代码

怎么样上面的代码运行成功没有？现在我们再来总结一下队列的概念。队列是一种特殊的线性结构，它只允许在队列的首部（head）进行删除操作称之为“出队”，而在队列的尾部（tail）进行插入操作称之为“入队”。当队列中没有元素时（即head==tail），称为空队列。在我们的日常生活中有很多情况都符合队列的特性。比如我们之前提到过的买票，每个排队买票的窗口就是一个队列。在这个队列当中，新来的人总是站在队列的最后面，来的越早的人越靠前也就越早能买到票，就是先来的人先服务，我们称为“先进先出”（First InFirst Out，FIFO）原则。

队列将是我们今后学习广度优先搜索以及队列优化的Bellman-Ford最短路算法的核心数据结构。所以现在将队列的三个基本元素（一个数组，两个变量）封装为一个结构体类型，如下。

struct queue
{
int data[100];//队列的主体，用来存储内容
int head;//队首
int tail;//队尾
};

复制代码

上面我们定义了一个结构体类型，我们通常将其放在main函数的外面，请注意结构体的定义末尾有个;号。struct是结构体的关键字，queue是我们为这个结构体起的名字。这个结构体有三个成员分别是：整型数组data、整型head和整型tail。这样我们就可以把这三个部分放在一起作为一个整体来对待。你可以这么理解：我们定义了一个新的数据类型，这个新类型非常强大，用这个新类型定义出的每一个变量可以同时存储一个整型数组和两个整数。

算法（5）：队列

有了新的结构体类型，如何定义结构体变量呢？很简单，这与我们之前定义变量的方式是一样，如下。

struct queue q;

复制代码

请注意struct queue需要整体使用，不能直接写queue q;这样我们就定义了一个结构体变量q。这个结构体变量q就可以满足队列的所有操作了。那又该如何访问结构体变量的内部成员呢？可以使用.号，它叫做成员运算符或者点号运算符，如下：

q.head=1;
q.tail=1;
scanf("%d",&q.data[q.tail]);

复制代码

好了，下面这段代码就是使用结构体来实现的队列操作。

#include <stdio.h>
struct queue
{
int data[100];//队列的主体，用来存储内容
int head;//队首
int tail;//队尾
};
int main()
{
struct queue q;
int i;
//初始化队列
q.head=1;
q.tail=1;
for(i=1;i<=9;i++)
{
//依次向队列插入9个数
scanf("%d",&q.data[q.tail]);
q.tail++;
}
while(q.head<q.tail) //当队列不为空的时候执行循环
{
//打印队首并将队首出队
printf("%d ",q.data[q.head]);
q.head++;
//先将新队首的数添加到队尾
q.data[q.tail]=q.data[q.head];
q.tail++;
//再将队首出队
q.head++;
}
getchar();getchar();
return 0;
}

复制代码

上面的这种写法看起来虽然冗余了一些，但是可以加强你对队列这个算法的理解。C++的STL库已经有队列的实现，有兴趣的同学可以参看相关材料。队列的起源已经无法追溯。在还没有数字计算机之前，数学应用中就已经有对队列的记载了。我们生活中队列的例子也比比皆是，比如排队买票，又或者吃饭时候用来排队等候的叫号机，又或者拨打银行客服选择人工服务时，每次都会被提示“客服人员正忙，请耐心等待”，因为客服人员太少了，拨打电话的客户需要按照打进的时间顺序进行等候等等。这里表扬一下肯德基的宅急送，没有做广告的嫌疑啊，每次一打就通，基本不需要等待。但是我每次打银行的客服（具体是哪家银行就不点名了）基本都要等待很长时间，总是告诉我“正在转接，请稍后”，嘟嘟嘟三声后就变成“客服正忙，请耐心等待！”然后就给我放很难听的曲子。看来钱在谁那里谁就是老大啊……

原文 http://www.linuxeden.com/html/news/20160509/166062.html

正文到此结束